半树的opencv笔记Day1

@[TOC]这真是份较为认真的打卡

Task01 OpenCV框架与图像插值算法

1.插值算法原理介绍
最近邻插值算法
双线性插值算法
2.OpenCV代码实践
cv.resize()各项参数及含义
3.实战咯
1+2：正正经经的基础理论知识复制黏贴嘿嘿
3：请一定跳到我最后去康康我搞出来的章鱼哥！！）

算法理论

在一幅输入图象$[u，v]$中，灰度值仅在整数位置上有定义。然而，输出图象[x，y]的灰度值一般由处在非整数坐标上的$（u，v）$值来决定。插值算法可以用来处理输入与输出间的转换问题，常见的插值算法有最近邻插值、双线性插值和三次样条插值。

1. 最近邻插值算法原理

   最近邻插值，是指将目标图像中的点，对应到源图像中后，找到最相邻的整数点，作为插值后的输出。（即在输入图像中找到对应的最相邻的整数点作为最后的确认值)
   1.1 小例子
   将一幅3X3的图像放大到4X4，用$f(x,y)$表示目标图像，$h(x,y)$表示原图像，公式如下：
   $$\begin{array}{c}f(ds{t}_X,ds{t}_Y)=h(\frac{ds{t}_{X}sr{c}_{Width}}{ds{t}_{Width}},\frac{ds{t}_{Y}sr{c}_{Height}}{ds{t}_{Height}})\end{array}$$$$\begin{array}{c}f(0,0)=h(0,0)f(0,1)=h(0,0.75)=h(0,1)f(0,2)=h(0,1.50)=h(0,2)f(0,3)=h(0,2.25)=h(0,2)...\end{array}$$
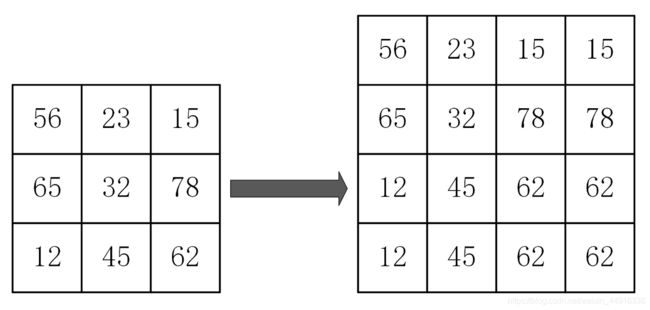
   不足之处： 用该方法作放大处理时，在图象中可能出现明显的块状效应。如图：
   

2. ** 双线性插值**

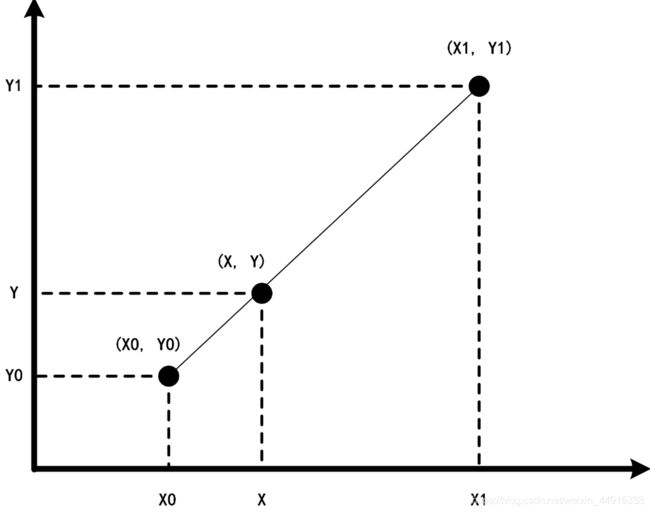
2.1线性插值，线性插值多项式和图片：

$$f(x)=a_{1}x+a_0$$
$$y=y_0+\left(x-x_0\right)\frac{y_1-y_0}{x_1-x_0}=y_0+\frac{\left(x-x_0\right)y_1-\left(x-x_0\right)y_0}{x_1-x_0}$$
2.2双线性插值
双线性插值就是线性插值在二维时的推广,在两个方向上做三次线性插值.
令$f(x，y)$为两个变量的函数，其在单位正方形顶点的值已知。假设我们希望通过插值得到正方形内任意点的函数值。则可由双线性方程: $$f(x,y)=ax+by+cxy+d$$
来定义的一个双曲抛物面与四个已知点拟合。
首先对上端的两个顶点进行线性插值得：

$$f(x,0)=f(0,0)+x[f(1,0)-f(0,0)]$$类似地，再对底端的两个顶点进行线性插值有： $$f(x,1)=f(0,1)+x[f(1,1)-f(0,1)]$$最后，做垂直方向的线性插值，以确定：

$$f(x,y)=f(x,0)+y[f(x,1)-f(x,0)]$$整理得：

$$\begin{array}{l}f(x,y)=[f(1,0)-f(0,0)]x+[f(0,1)-f(0,0)]y+[f(1,1)+f(0,0)-f(0,1)-f(1,0)]xy+f(0,0)\end{array}$$
3. 映射方法
3.1向前映射法

可以将几何运算想象成一次一个象素地转移到输出图象中。如果一个输入象素被映射到四个输出象素之间的位置，则其灰度值就按插值算法在4个输出象素之间进行分配。称为向前映射法，或象素移交影射。
注：从原图象坐标计算出目标图象坐标镜像、平移变换使用这种计算方法

3.2向后映射法

向后映射法（或象素填充算法）是输出象素一次一个地映射回到输入象素中，以便确定其灰度级。如果一个输出象素被映射到4个输入象素之间，则其灰度值插值决定，向后空间变换是向前变换的逆。
注：从结果图象的坐标计算原图象的坐标
旋转、拉伸、放缩可以使用
解决了漏点的问题，出现了马赛克

5. 实战
   代码展示

import cv2
from matplotlib import pyplot as plt
img = cv2.imread('imagesFor_try5.png',cv2.IMREAD_UNCHANGED)
#获取原图像规格
print(img.shape)  #print out:(185,273,3)
scale_percent = 30
width = int(img.shape[1]*scale_percent/100)
height = int(img.shape[0]*scale_percent/100)
dim = (width,height)

#cv.INTER_LINEAR	双线性插值 处理img
#interpolation	【可选】插值方式
resized = cv2.resize(img,dim,interpolation = cv2.INTER_LINEAR) 

fx = 1.5 #沿水平轴的比例因子(可选
fy = 1.5 #沿垂直轴的比例因子（可选

#cv.INTER_NEAREST	最近邻插值 处理img
resized1 = cv2.resize(resized,dsize = None,fx = fx,fy =fy,interpolation = cv2.INTER_NEAREST)

#cv.INTER_LINEAR	双线性插值 这里跟resized那一部分不同的就是添加了 fx 和 fy ~(对比了一下，加了fx fy我的章鱼哥更模糊叻
resized2 = cv2.resize(resized,dsize = None,fx = fx,fy =fy,interpolation = cv2.INTER_LINEAR)
#cv.INTER_CUBIC	基于4x4像素邻域的3次插值法
resized3 = cv2.resize(resized,dsize = None,fx = fx,fy =fy,interpolation = cv2.INTER_CUBIC)
#cv.INTER_AREA	基于局部像素的重采样
resized4 = cv2.resize(resized,dsize = None,fx = fx,fy =fy,interpolation = cv2.INTER_AREA)
print(resized.shape) #out:(55,81,3)
#show all the images SHOW_TIME Biubiubiu
plt.imshow(img)
plt.figure()
plt.imshow(resized)
plt.figure()
plt.imshow(resized1)
plt.figure()
plt.imshow(resized2)
plt.figure()
plt.imshow(resized3)
plt.figure()
plt.imshow(resized4)

结果截图展示


最后cv.INTER_CUBIC 基于4x4像素邻域的3次插值法和cv.INTER_AREA 基于局部像素的重采样显示的图片~

(haha 章鱼哥逐渐模糊 ps:上传个图片简直是要耗光我所有的耐心orz不过没关系，再麻烦都没事！！我做出来的章鱼哥不允许你们没有见过！！）

请参考这位大佬的CSDN！！