9.4 分段双立方插值

示例

  前文讲了分段立方插值，现在加了个双，这个双是什么意思？就是双变量的意思。也就是立体几何领域的立方插值。我举个实际场景的例子，对地形进行采样，取不同点的高度，最后回归整个地区的地形。假设这是采样数据：

x y z
0 0 5
0 5 3
0 10 5
5 0 3
5 5 10
5 10 3
10 0 5
10 5 3
10 10 5

  用plot软件(gnuplot/pgfplot/python皆可)进行3D绘制，可以大致看看这九个点的位置，例如我用LaTex绘制，这九个点是这样的：

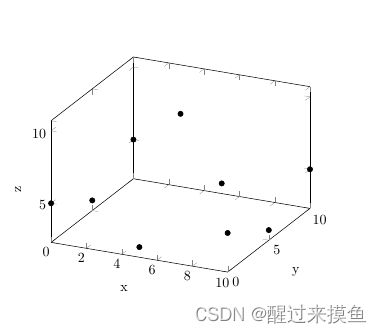
  双立方插值是回归出分片的曲面，经过这些点，而且相邻两个区域的曲面平滑过渡。对上诉采样点进行插值后的四块曲面就是下图的样子：

系数矩阵

  双立方函数的表达式是非常复杂的，以上例第一个分段为例子，它的方程是这样的：
$$\begin{gathered} z=f(x,y)=5-6(y/5{)}^2+4(y/5{)}^3 \\ +(-6+81(y/5{)}^2-54(y/5{)}^3)(x/5{)}^2 \\ +(4-54(y/5{)}^2+36(y/5{)}^3)(x/5{)}^3 \end{gathered}$$
  方程很长，计算很繁琐，也不好看，对于二元多项式，智慧的劳动人民发明了系数矩阵。那么怎么用系数矩阵呢？只需要像我这样：
$$z=f(x,y)=\left[\begin{array}{cccc}5& 0& -6& 4\\ 0& 0& 0& 0\\ -6& 0& 81& -54\\ 4& 0& -54& 36\end{array}\right]\times \left[\begin{array}{c}1\\ \frac{y}{5}\\ (\frac{y}{5}{)}^2\\ (\frac{y}{5}{)}^3\end{array}\right]\cdot \left[\begin{array}{c}1\\ \frac{x}{5}\\ (\frac{x}{5}{)}^2\\ (\frac{x}{5}{)}^3\end{array}\right]$$
  也就是用矩阵先叉乘$y$系数向量，再点乘$x$系数向量得到的点积来表示曲面方程。用矩阵表示，有两个好处，第一，看起来神清气爽，第二，计算机求值方便。所以上例中的分段曲面可以用系数矩阵表示为：
$$z=f(x,y)=\{\begin{array}{l}\left[\begin{array}{cccc}5& 0& -6& 4\\ 0& 0& 0& 0\\ -6& 0& 81& -54\\ 4& 0& -54& 36\end{array}\right]\times \left[\begin{array}{c}1\\ \frac{y}{5}\\ (\frac{y}{5}{)}^2\\ (\frac{y}{5}{)}^3\end{array}\right]\cdot \left[\begin{array}{c}1\\ \frac{x}{5}\\ (\frac{x}{5}{)}^2\\ (\frac{x}{5}{)}^3\end{array}\right]x\in [0,5],y\in [0,5]\\ \left[\begin{array}{cccc}3& 0& 21& -14\\ 0& 0& 0& 0\\ 6& 0& -81& 54\\ -4& 0& 54& -36\end{array}\right]\times \left[\begin{array}{c}1\\ \frac{y-5}{5}\\ (\frac{y-5}{5}{)}^2\\ (\frac{y-5}{5}{)}^3\end{array}\right]\cdot \left[\begin{array}{c}1\\ \frac{x}{5}\\ (\frac{x}{5}{)}^2\\ (\frac{x}{5}{)}^3\end{array}\right]x\in [0,5],y\in [5,10]\\ \left[\begin{array}{cccc}3& 0& 6& -4\\ 0& 0& 0& 0\\ 21& 0& -81& 54\\ -14& 0& 54& -36\end{array}\right]\times \left[\begin{array}{c}1\\ \frac{y}{5}\\ (\frac{y}{5}{)}^2\\ (\frac{y}{5}{)}^3\end{array}\right]\cdot \left[\begin{array}{c}1\\ \frac{x-5}{5}\\ (\frac{x-5}{5}{)}^2\\ (\frac{x-5}{5}{)}^3\end{array}\right]x\in [5,10],y\in [0,5]\\ \left[\begin{array}{cccc}10& 0& -21& 14\\ 0& 0& 0& 0\\ -21& 0& 81& -54\\ 14& 0& -54& 36\end{array}\right]\times \left[\begin{array}{c}1\\ \frac{y-5}{5}\\ (\frac{y-5}{5}{)}^2\\ (\frac{y-5}{5}{)}^3\end{array}\right]\cdot \left[\begin{array}{c}1\\ \frac{x-5}{5}\\ (\frac{x-5}{5}{)}^2\\ (\frac{x-5}{5}{)}^3\end{array}\right]x\in [5,10],y\in [5,10]\end{array}$$

求系数矩阵

  最后的工作就是求系数矩阵了。而这是最难最复杂的部分。首先我们看其中一个网格：

  根据样本数据，我们可以求得四个点的函数值、四个点的x偏导数，y偏导数以及这两个偏导数的乘积，这16个值可以求得系数矩阵的16个值，也就是解十六元一次方程。这里我就不写求解过程和推导过程了，只讲如何计算。
  二元函数的梯度(注意是nabla符号$\nabla$不是大写希腊字母$\Delta$)是：
$$\nabla f(x,y)=\left[\begin{array}{c}\frac{\partial f(x,y)}{\partial x}\\ \frac{\partial f(x,y)}{\partial y}\end{array}\right]$$
  采样点组成了网格，对于网格的边缘的采样点，偏导数、偏导数乘积全部为0。对于远离边缘的采样点，我们这样用差分作为偏导数，这样求值：
$$\nabla f(x_i,y_j)=\left[\begin{array}{c}\frac{f(x_{i+1},y_j)-f(x_{i-1},y_j)}{x_{i+1}-x_{i-1}}\\ \frac{f(x_i,y_{j+1})-f(x_i,y_{j-1})}{y_{i+1}-y_{i-1}}\end{array}\right]$$
  因为是插值，所以把差分当作偏导数的值，而偏导乘积可以这样计算：
$$\frac{d^{2}f(x_i,y_j)}{d{x}_{i}d{y}_j}=\frac{f(x_{i+1},y_{j+1})+f(x_{i-1},y_{j-1})-f(x_{i-1},y_{j+1})-f(x_{i+1},y_{j-1})}{(x_{i+1}-x_{i-1})(y_{i+1}-y_{i-1})}$$
  就这样计算出了三个二维数组，暂且命名为dx,dy,dxdy三个二维数组。然后函数值和这三个数组组成一个一个16个元素的向量$\beta$。假设每个定义域分片的四个订点为$(0,0),(0,1),(1,0),(1,1)$，那么这个长度为16的向量就是这个样子的：
$$\beta =\left[\begin{array}{c}f(0,0)\\ f(1,0)\\ f(0,1)\\ f(1,1)\\ d_{x}f(0,0)\\ d_{x}f(1,0)\\ d_{x}f(0,1)\\ d_{x}f(1,1)\\ d_{y}f(0,0)\\ d_{y}f(1,0)\\ d_{y}f(0,1)\\ d_{y}f(1,1)\\ d_{xy}f(0,0)\\ d_{xy}f(1,0)\\ d_{xy}f(0,1)\\ d_{xy}f(1,1)\end{array}\right]$$
  然后$\beta$向量放在标准双立方插值矩阵右边点乘一下得到一个转置的向量。这个转置的向量是由系数矩阵的元素组成，公式如下：
$$\left[\begin{array}{cccccccccccccccc}1& 0& -3& 2& 0& 0& 0& 0& -3& 0& 9& -6& 2& 0& -6& 4\\ 0& 0& 3& -2& 0& 0& 0& 0& 0& 0& -9& 6& 0& 0& 6& -4\\ 0& 0& 0& 0& 0& 0& 0& 0& 3& 0& -9& 6& -2& 0& 6& -4\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 9& -6& 0& 0& -6& 4\\ 0& 1& -2& 1& 0& 0& 0& 0& 0& -3& 6& -3& 0& 2& -4& 2\\ 0& 0& -1& 1& 0& 0& 0& 0& 0& 0& 3& -3& 0& 0& -2& 2\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 3& -6& 3& 0& -2& 4& -2\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -3& 3& 0& 0& 2& -2\\ 0& 0& 0& 0& 1& 0& -3& 2& -2& 0& 6& -4& 1& 0& -3& 2\\ 0& 0& 0& 0& 0& 0& 3& -2& 0& 0& -6& 4& 0& 0& 3& -2\\ 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 3& -2& 1& 0& -3& 2\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -3& 2& 0& 0& 3& -2\\ 0& 0& 0& 0& 0& 1& -2& 1& 0& -2& 4& -2& 0& 1& -2& 1\\ 0& 0& 0& 0& 0& 0& -1& 1& 0& 0& 2& -2& 0& 0& -1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& -1& 2& -1& 0& 1& -2& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& -1& 0& 0& -1& 1\end{array}\right]\cdot \beta ={\left[\begin{array}{c}{c}_{0,0}\\ c_{1,0}\\ c_{2,0}\\ c_{3,0}\\ c_{0,1}\\ c_{1,1}\\ c_{2,1}\\ c_{3,1}\\ c_{0,2}\\ c_{1,2}\\ c_{2,2}\\ c_{3,2}\\ c_{0,3}\\ c_{1,3}\\ c_{2,3}\\ c_{3,3}\end{array}\right]}^T$$
  而c矩阵就是我们最终获得的系数矩阵。公式过程如此复杂，强烈建议收藏我的博客，顺便关注一波。

Python实现

  双立方插值函数类：

# _*_ coding:utf-8 _*_

class BiVariablesFunction:

    def __init__(self, matrix, x_domain, y_domain):
        self.__matrix = matrix
        self.__x_domain = x_domain
        self.__y_domain = y_domain

    def __call__(self, *args, **kwargs):
        x = args[0]
        y = args[1]
        x = (x - self.__x_domain[0]) / (self.__x_domain[1] - self.__x_domain[0])
        y = (y - self.__y_domain[0]) / (self.__y_domain[1] - self.__y_domain[0])
        # 系数矩阵 * y幂向量*x幂向量
        y_power = [1, y, y * y, y * y * y]
        x_power = [1, x, x * x, x * x * x]
        temp = [0, 0, 0, 0]
        result = 0
        for i in range(0, 4):
            line = self.__matrix[i]
            r = 0
            for j in range(0, len(y_power)):
                r += line[j] * y_power[j]
            result += r * x_power[i]
        return result


def index_of(values, x):
    for i in range(0, len(values) - 1):
        if values[i] <= x <= values[i + 1]:
            return i
    pass


class BiVariablesFunctions:

    def __init__(self, functions, x_values, y_values):
        self.__functions = functions
        self.__x_values = x_values
        self.__y_values = y_values

    def __call__(self, *args, **kwargs):
        x = args[0]
        y = args[1]
        index_x = index_of(self.__x_values, x)
        index_y = index_of(self.__y_values, y)
        return self.__functions[index_x][index_y](x, y)

  插值类：

# _*_ coding:utf-8 _*_

from com.youngthing.mathalgorithm.interpolation.bivar_function import BiVariablesFunction, BiVariablesFunctions

AINV = [
    [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [-3, 3, 0, 0, -2, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [2, -2, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, -3, 3, 0, 0, -2, -1, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 2, -2, 0, 0, 1, 1, 0, 0],
    [-3, 0, 3, 0, 0, 0, 0, 0, -2, 0, -1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, -3, 0, 3, 0, 0, 0, 0, 0, -2, 0, -1, 0],
    [9, -9, -9, 9, 6, 3, -6, -3, 6, -6, 3, -3, 4, 2, 2, 1],
    [-6, 6, 6, -6, -3, -3, 3, 3, -4, 4, -2, 2, -2, -2, -1, -1],
    [2, 0, -2, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 2, 0, -2, 0, 0, 0, 0, 0, 1, 0, 1, 0],
    [-6, 6, 6, -6, -4, -2, 4, 2, -3, 3, -3, 3, -2, -1, -2, -1],
    [4, -4, -4, 4, 2, 2, -2, -2, 2, -2, 2, -2, 1, 1, 1, 1]
]


def interpolate(x_values, y_values, f_values):
    # 初始化三个数组

    dx, dy, dx_dy = diffs(x_values, y_values, f_values)
    n = len(x_values) - 1
    functions = [[None for _ in range(0, n)] for _ in range(0, n)]
    for i in range(0, n):
        diff_x = x_values[i + 1] - x_values[i]
        for j in range(0, n):
            diff_y = y_values[j + 1] - y_values[j]
            beta = [
                f_values[i][j], f_values[i + 1][j], f_values[i][j+1], f_values[i+1][j + 1],
                dx[i][j] * diff_x, dx[i + 1][j] * diff_x, dx[i][j] * diff_x, dx[i][j + 1] * diff_x,
                dy[i][j] * diff_x, dy[i + 1][j] * diff_x, dy[i][j] * diff_x, dy[i][j + 1] * diff_x,
                dx_dy[i][j] * diff_y, dx_dy[i + 1][j] * diff_y, dx_dy[i][j] * diff_y, dx_dy[i][j + 1] * diff_y,
            ]
            functions[i][j] = BiVariablesFunction(coefficients(beta),
                                                  [x_values[i], x_values[i + 1]],
                                                  [y_values[j], y_values[j + 1]])
    return BiVariablesFunctions(functions, x_values, y_values)


def coefficients(beta):
    n = 16
    coeff = [0] * n
    for i in range(0, n):
        row = AINV[i]
        r = 0
        for j in range(0, n):
            r += row[j] * beta[j]
        coeff[i] = r
    result = [[0] * 4 for _ in range(0, 4)]
    for i in range(0, n):
        result[i % 4][i // 4] = coeff[i]
    return result


def diffs(x_values, y_values, f_values):
    n = len(x_values)

    dx = [[0 for _ in range(0, n)] for _ in range(0, n)]
    dy = [[0 for _ in range(0, n)] for _ in range(0, n)]
    dx_dy = [[0 for _ in range(0, n)] for _ in range(0, n)]
    for i in range(1, n - 1):
        diff_x = x_values[i + 1] - x_values[i - 1]
        for j in range(1, n - 1):
            diff_y = y_values[j + 1] - y_values[j - 1]
            dy[i][j] = (f_values[i][j + 1] - f_values[i][j - 1]) / diff_y
            dx[i][j] = (f_values[i + 1][j] - f_values[i - 1][j]) / diff_x
            dx_dy[i][j] = (f_values[i + 1][j + 1] + f_values[i - 1][j - 1]
                           - f_values[i - 1][j + 1] - f_values[i + 1][j - 1]) / (diff_x * diff_x)
    return dx, dy, dx_dy

测试

  测试类:

import unittest

from com.youngthing.mathalgorithm.interpolation.bicubic_spline import *


class MyTestCase(unittest.TestCase):
    def test_1(self):
        x_values = [0, 5, 10]
        y_values = [0, 5, 10]
        f_values = [[5, 3, 5],
                    [3, 10, 3],
                    [5, 3, 5]]
        functions = interpolate(x_values, y_values, f_values)
        for x in x_values:
            for y in y_values:
                print(f'f({x},{y})=', functions(x, y))
        print(functions(3, 3))

    def test_2(self):
        x_values = [0, 5, 10]
        y_values = [0, 4, 8]
        f_values = [[5, 3, 5],
                    [3, 10, 3],
                    [5, 3, 5]]
        functions = interpolate(x_values, y_values, f_values)
        for x in x_values:
            for y in y_values:
                print(f'f({x},{y})=', functions(x, y))
        print(functions(3, 3))


if __name__ == '__main__':
    unittest.main()

  测试结果完全正确：

f(0,0)= 5.0
f(0,5)= 3.0
f(0,10)= 5.0
f(5,0)= 3.0
f(5,5)= 10.0
f(5,10)= 3.0
f(10,0)= 5.0
f(10,5)= 3.0
f(10,10)= 5.0
6.187136000000001
f(0,0)= 5.0
f(0,4)= 3.0
f(0,8)= 5.0
f(5,0)= 3.0
f(5,4)= 10.0
f(5,8)= 3.0
f(10,0)= 5.0
f(10,4)= 3.0
f(10,8)= 5.0
6.93725