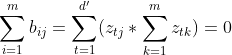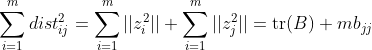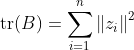降维与度量学习
入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。
目录
一、降维
1、需要降维的原因
2、降维定义
3、为什么能降维？
4、经典降维方法——多维缩放（MDS）
（1）主要要求
（2）原理推导
（3）算法步骤
5、降维方法——线性降维方法
6、降维效果的评估
二、主成分分析（PCA）
1、算法目的
2、算法推导
3、算法步骤
4、python实现
5、优缺点
（1）优点
（2）缺点
三、核化线性降维（KPCA）
1、原理推导
2、python实现KPCA
三、流形学习
1、流形
2、为什么需要流形学习
3、常见的流形学习方法一 —— 等度量映射（Isomap）
（1）基本出发点
（2）计算测地线距离
（3）降维
（4）不足
4、常见的流形学习方法二 —— 局部线性嵌入（LLE）
（1）出发点
（2）算法推导
（3）算法步骤
四、度量学习
1、度量与度量学习的简单介绍
（1）度量与度量学习
（2）降维需要度量学习的原因
2、带参数的距离度量——马氏距离
3、 近邻成分分析（NCA）
一、降维
1、需要降维的原因
样本的特征数也称为维数，当维数非常大时，也就是通常所说的“维数灾难”。这具体表现在：在高维情形下，数据样本变得十分稀疏（因为此时要满足训练样本为“密采样”的总体样本数目是一个天文数字）。训练样本的稀疏使得其代表总体分布的能力大大减弱，从而削弱了学习器的泛化能力；同时当维数很高时，计算距离也变得十分复杂，这也是为什么SVM使用核函数 “低维计算，高维表达” 的原因。
2、降维定义
缓解维数灾难的一个重要途径就是降维，即通过某种数学变换将原始高维空间转变到一个低维的子空间。这样在子空间中样本密度就会增大，距离计算也会比之前简单。
3、为什么能降维？
往往我们得到的数据是多维的，但与学习任务密切相关的也许仅是某个低维分布（即高维空间中的一个低维嵌入）。
4、经典降维方法——多维缩放（MDS）
（1）主要要求
要求原始空间中样本之间的距离在低维空间中得以保持。
（2）原理推导
已知：假设m个样本在原始空间的距离矩阵为D，其中第 i 行 j 列的元素
为样本 
到 
的距离。
目标：获得样本在d'维空间的表示
，d'
求解：令B为降维后样本的内积矩阵，
，其中
，则：
令降维后的样本Z被中心化，即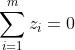
。因此有B的行与列之和均为0，即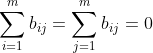
因为
；
所以有：
同理得：
其中矩阵B的迹：
令：
由上述6道式子整合得：
进一步化简得：
由上述式子我们即通过降维前的距离矩阵D求出降维后距离也不变的d‘维空间的原数据表示矩阵Z的内积矩阵B。
为了从B推出Z，我们对B做特征值分解，
，其中 
为特征值构成的对角矩阵，且
，V为特征向量矩阵。假定其中有d*个非零特征值，他们构成对角矩阵
，令
表示其相应的特征向量矩阵，则Z可表示为：
在现实应用中为了有效降维，往往仅需降维后的距离与原始空间中的距离尽可能接近，不必严格相等。此时可取 d’ << d 个最大特征值构成对角矩阵
，令
表示相应的特征向量矩阵，则Z最终可表示为：
。
（3）算法步骤
输入: 距离矩阵
，其元素 为样本 到 的距离，降维后的维数为d'。
A、根据（1）（2）（3）式子计算
；
B、根据（4）计算矩阵B；
C、对B做特征值分解；
D、取
为d'个最大特征值所构成的对角矩阵，为相应的特征向量矩阵
输出：
，每行是一个样本的低维坐标
5、降维方法——线性降维方法
为了得到低维子空间，最简单的方法是对原始空间进行线性变换（d->d’维），即：
W即为d*d‘的变换矩阵，即W为正交变换，包含d’个d维基向量。
常见的线性降维方法有：PCA，
6、降维效果的评估
比较降维前后学习器的性能。
若降维到2，3维则可通过可视化技术来直观判断降维结果。
二、主成分分析（PCA）
1、算法目的
经过线性变换，将数据从d维线性空间映射至 d‘ 维（d’ < d），并且期望在投影方向上信息量最大（最大可分性），同时将数据进行反向重构时代价最小（最近重构性）。
最大可分性：样本点在超平面（用该超平面对所有样本进行描述）上的投影尽可能分开；
最近重构性：样本点到超平面的距离都尽可能的近；
2、算法推导
已知与数据假设：原始样本为d维，目标降维为d‘维，假设投影变换后得到的新坐标系为
，其中
是标准正交基，因此有
。
求解方法（从最大可分性角度出发）：
目标：最大可分即要求所有样本点的投影尽可能地分开，即投影后样本点的方差最大化。
3、算法步骤
（1）对所有特征进行中心化：去均值
（2）求协方差矩阵
（3）求协方差矩阵的特征值和相对应的特征向量
（4）取最大的d’个特征值所对应的特征向量构成最终的投影矩阵
4、python实现
以鸢尾花数据为例，将4维数据降维到2维
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
data=load_iris()
x=data.data
y=data.target
#print(x.shape)
pca=PCA(n_components=2) #加载PCA算法，设置降维后主成分数目为2
# n_components=‘mle’，将自动选取主成分个数n，使得满足所要求的方差百分比
# n_components=None，返回所有主成分
reduced_x=pca.fit_transform(x)#对样本进行降维，即将数据X转换成降维后的数据
#print(reduced_x.shape)
print(pca.explained_variance_ )# 贡献方差，即特征根
print(pca.explained_variance_ratio_)#返回所保留的n个成分各自的方差百分比(每个主成分保留的方差百分比),这里可以理解为单个变量方差贡献率
print(pca.components_ )# 成分矩阵(返回协方差矩阵的特征向量,即W^T)
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]
for i in range(len(reduced_x)):
if y[i] ==0:
red_x.append(reduced_x[i][0])
red_y.append(reduced_x[i][1])
elif y[i]==1:
blue_x.append(reduced_x[i][0])
blue_y.append(reduced_x[i][1])
else:
green_x.append(reduced_x[i][0])
green_y.append(reduced_x[i][1])
#可视化
plt.scatter(red_x,red_y,c='r',marker='.')
plt.scatter(blue_x,blue_y,c='b',marker='.')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()result:
5、优缺点
（1）优点
通过PCA降维之后的各个主成分之间是正交的，可以消除原始数据之间相互影响的因素；
计算过程并不复杂，实现起来较简单容易；
在保留大部分主要信息的前提下，起到了降维效果；
在一定程度上起到去噪的作用；
（2）缺点
主成分特征维度的含义具有模糊性，解释性差（新坐标基底所代表的含义未知）；
PCA降维的标准是选取令原数据在新坐标轴上方差最大的主成分。但方差小的特征就不一定不重要，这样的唯一标准有可能会损失一些重要信息；
只保留特定百分比的主成分，属于“有损压缩”，难免会损失一些信息；
三、核化线性降维（KPCA）
1、原理推导
前面提到的线性降维的假设是：从高维空间到低维空间的函数映射是线性的。然而，现实任务中大多数可能需要非线性映射才能找到恰当的低维嵌入。
基于核技巧对线性降维方法进行“核化”是非线性降维常用方法之一，核主成分分析是其中之一。
即把X变为
，然后再套进原先的线性降维方法中去。
这样既可以避开求W，又可以避开直接求具体的
，实现通过求的内积K和求K的特征向量来得到降维后的样本点。
2、python实现KPCA
import matplotlib.pyplot as plt
from sklearn.decomposition import KernelPCA
from sklearn.datasets import make_circles
X,y=make_circles(n_samples=100, shuffle=True, random_state=None, factor=0.8)
scikit_kpca=KernelPCA(n_components=2,kernel='rbf',gamma=15)#选择高斯核函数
X_pre=scikit_kpca.fit_transform(X)#映射
#可视化
plt.scatter(X_pre[y==0,0],X_pre[y==0,1],color='red',marker='o',alpha=0.5,s=8)
plt.scatter(X_pre[y==1,0],X_pre[y==1,1],color='blue',marker='o',alpha=0.5,s=8)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()result：
三、流形学习
1、流形
具有不同维数的任意光滑的曲线或曲面，局部具有欧几里得空间性质的空间，即是弯曲的N实数描述的点集合。
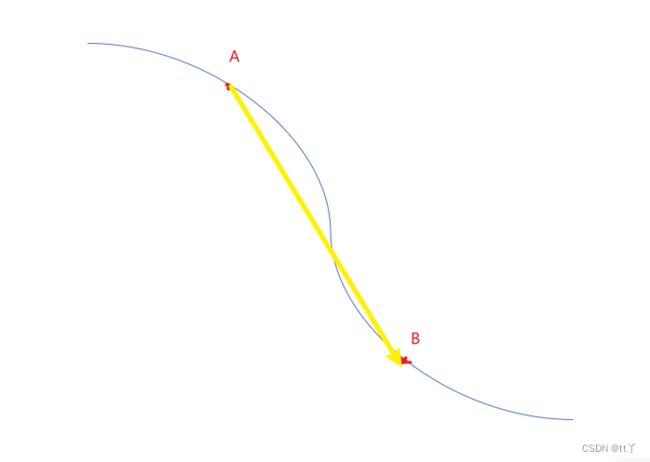
流形的两点间的距离的定义是：
邻近的两点，其距离是坐标差的平方相加再开根号（即普通的欧氏距离定义）。
遥远的两点求其距离，需先在中途铺设多点形成路径，以点点相连为路径长，取最短的路径长定义为距离。如下图所示：
AB两点间的距离不是传统的欧氏距离（即黄色线），而是蓝色线。
2、为什么需要流形学习
流形学习是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据的内在规律。
3、常见的流形学习方法一 —— 等度量映射（Isomap）
（1）基本出发点
保持近邻样本间距离不变。
低维流形嵌入到高维空间之后，直接在高维空间中计算直线距离具有误导性，因为高维空间中的直线距离在低维嵌入流形上是不可达的。低维嵌入流形上两点间的距离是“测地线”距离，是两点之间的本真距离。直接在高维空间中计算直线距离是不正确的。
（2）计算测地线距离
流形在局部上与欧氏空间同胚，利用这个性质对每个点基于欧氏距离找出其近邻点，建立一个近邻连接图（k近邻图——指定近邻点的个数或ϵ近邻图——指定距离的阈值）。这样我们就将计算两点间测地线距离的问题转化为解决近邻连接图上两点间最短路径的问题。
最短路径问题可以用Dijkstra（贪心思路）或者Floyd算法求最短路径。
（3）降维
通过上面的方法得到任意两点间的本真距离后再使用MDS方法实现降维，获取样本点在低维空间的坐标。
（4）不足
A、Isomap只是得到了训练样本在低维空间的坐标，现在来个新的样本点不能直接得到它的低维空间坐标。需要额外训练一个回归学习器（输入：高维样本点坐标；输出：得到的低维样本点坐标）进行预测。
B、k近邻图或ϵ近邻图都存在一定的问题：短路，断路。
4、常见的流形学习方法二 —— 局部线性嵌入（LLE）
（1）出发点
保持邻域内样本之间的线性关系（即局部线性重构）。
假定样本点 的坐标能够通过它的邻域样本
进行线性组合而重构出来，即：
LLE算法希望这种关系在低维空间中得到保持。
（2）算法推导
A、先求线性重构中的权重系数
B、已知W求降维后的坐标Z
这里取最小的特征值是因为我们希望他们间的差距更小，所以选方差贡献小的，作为我们的新坐标（这里要和PCA——最大可分，区分开）。
（3）算法步骤
输入数据集X，设置近邻参数k，降维后的维数为d‘
A、找到每个点的k近邻
B、通过
求解W
C、进而得到M
D、对M进行特征值分解，取最小的前d’个特征值对应的特征向量构成
四、度量学习
1、度量与度量学习的简单介绍
（1）度量与度量学习
一个度量（距离函数）是一个定义集合中元素之间距离的函数。一个具有度量的集合被称为度量空间。
度量学习即相似度学习。
（2）降维需要度量学习的原因
数据降维的目的是找到一个合适的低维空间进行学习，一个空间对应的就是在样本属性上定义的一个距离度量。所以将问题转化为寻找一个合适的距离度量——直接”学习“出一个合适的距离度量。
2、带参数的距离度量——马氏距离
为什么要带参数的原因：带参数才可以学习，固定不能学习。
马氏距离可以看作是欧氏距离的一种修正，修正了欧式距离中各个维度尺度不一致且相关的问题（即每个维度的距离权重不同）。
3、 近邻成分分析（NCA）
NCA虽然借助使用了分类器KNN，但是NCA并不是做分类问题的，而是度量学习和降维，找到一个合适的M（
）。
然后根据一些限定条件算出P
欢迎大家在评论区批评指正，谢谢~