内孔照明方式仿真和图像展开径向误差消除20221120
目录
内孔检测系统成像照明方式仿真
(1) 直接照明
(2) 背光照明
(3) 同轴照明
(4) 期望照明方式
内孔图像展开径向畸变消除
内孔检测系统成像照明方式仿真
在发动机内壁成像过程中,所采用的照明方式将直接影响所采集到的图像的质量,而在机器视觉中常用的照明方式由直接照明、背光照明以及同轴照明。我们采用LightTools仿真软件可以初步的模拟真实的发动机内孔的光照情况。
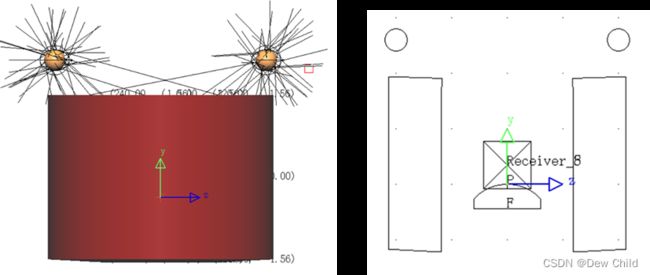
(1) 直接照明
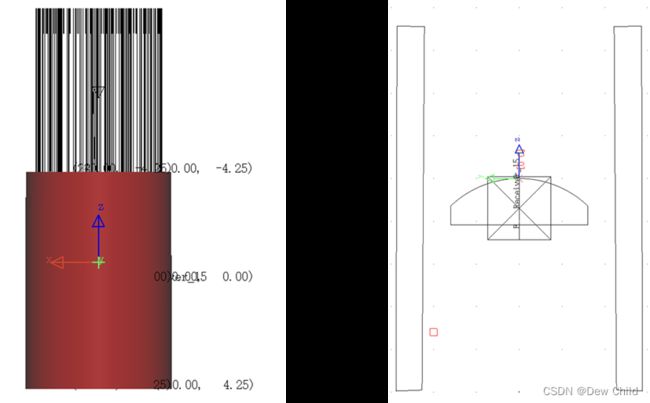
光直接照射向物体,但是在发动机内壁检测过程中,由于发动机壁会遮挡部分光,所以这种照明方式将导致发动机内壁靠近顶部区域较亮同时底部区域较暗,不适合整体成像。
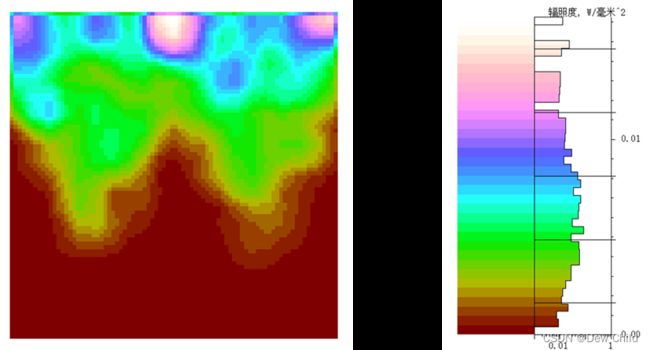
可以看出,圆柱体的上部分的光照较强,而下部分几乎没有光照。
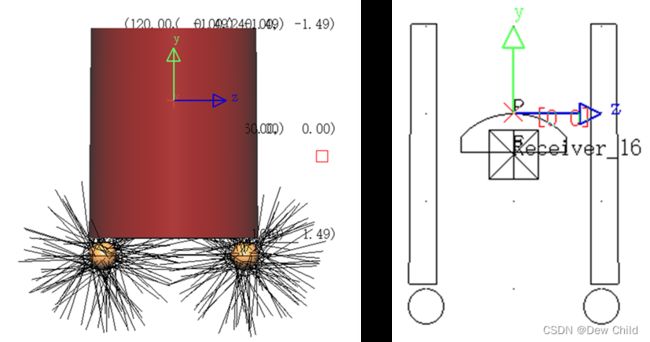
(2) 背光照明
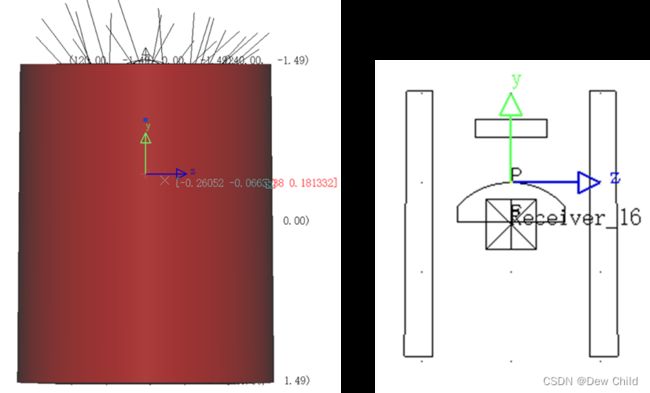
光从发动机内孔底部发射,但是在发动机内壁检测过程中,由于发动机壁会遮挡部分光,所以这种照明方式将导致发动机内壁靠近底部区域较亮同时顶部区域较暗,不适合整体成像。同时,这种方法只适合通孔工件。
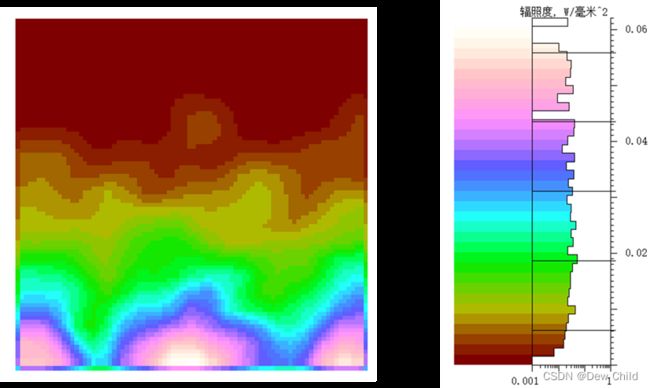
可以看出,圆柱体工件内壁的下部分的光照较强,而上部分几乎没有光照。
(3) 同轴照明
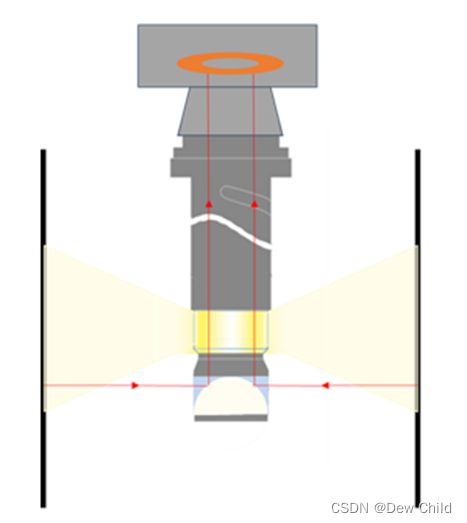
同轴光的形成——通过垂直墙壁出来的变化发散光,射到一个使光向下的分光镜上,相机从上面通过分光镜看物体。这种方式可以随着相机系统在工件不同位置为工件照明,但是由于采用的球面反射镜照明,所以同轴光反射后照射在工件内壁并不均匀。而在仿真过程中,我们只需要对内孔径向输入平行光就能模拟出同轴光照明的情况。
可以看出,在经过同轴光源照明的内孔壁会在光线刚经由球面反射镜反射后的部分区域亮度极高,而其他区域的亮度却很低,不利于成像和观测。
(4) 期望照明方式
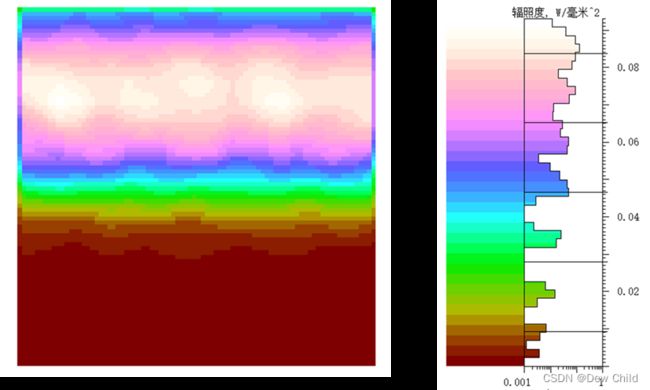
以上三种常用的照射方式对于发动机内壁成像都并不是很理想,我们期望设计一种照明方式,可以使得其照明能跟随相机移动,同时使成像的光照相对均匀。为此,我们设计了LED灯珠紧贴视窗内壁环形排列,视窗为亚克力磨砂材质的照射方式。在模拟的时候我们可以在反射镜的上方添加环带型光源。
可以看出,此种方式和同轴光源相比在某一固定位置上,照射到内孔表面的光照更加均匀,跟适合我们进行成像。这样,经由亚克力磨砂材质透过的LED光线将较为均匀地照射到工件内壁区域。
内孔图像展开径向畸变消除
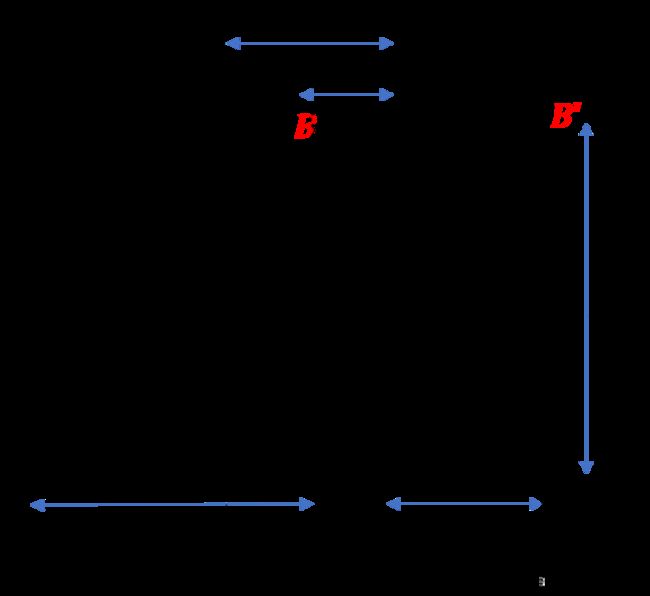
由于本课题中采用的是球面反射镜对发动机工件内壁图像进行成像,所以除了在所呈圆环图像的周向上存在畸变,其在圆环图像上的径向上也会存在畸变,所以我们根据反射原理以及反射镜参数初步消除径向误差,其基本原理如图所示。
同样,在这里我们假设已经展开的矩形图像的上的一点B,经过图像变换去径向畸变后的坐标为B',满足基本的反射原理,这样我们就能复原出内孔壁的真实图像,根据图中的参数建立其几何关系如下。
![]()
进一步推算出图像去畸变后的坐标结果。
![]()
其中
根据这个坐标映射关系,我们能得到初步的去畸变图像。
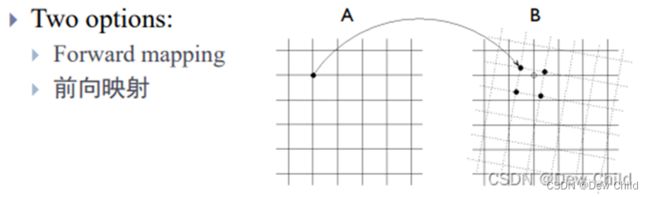
正如前文所描述的图像变换的映射关系而言,这里我们只采用了前向映射。
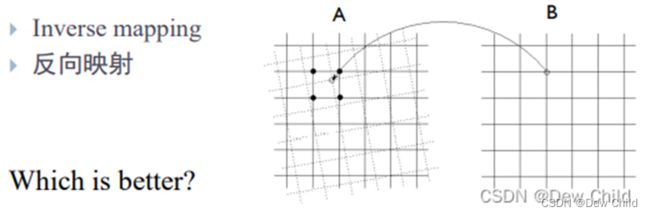
并且没有插值,这也就导致了变换后的图像部分网格点上并没有像素的灰度值定义(默认灰度为0),所以图像中存在部分黑色的线条,为了消除这种情况,我们需要采用后向映射的方式。
并对变换后的网格点中的每一个像素灰度值进行插值,这里我们采用双线性插值的方法。
针对这个双线性插值示意图的具体的双线性插值的公式可表示为
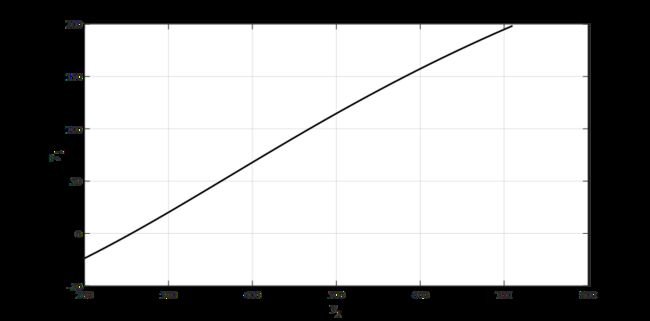
而在插值的过程中,我们需要的是变换后坐标关于变换前坐标的函数(即y2关于y1的函数),而前文中的公式推导只能得到y1关于y2的函数。
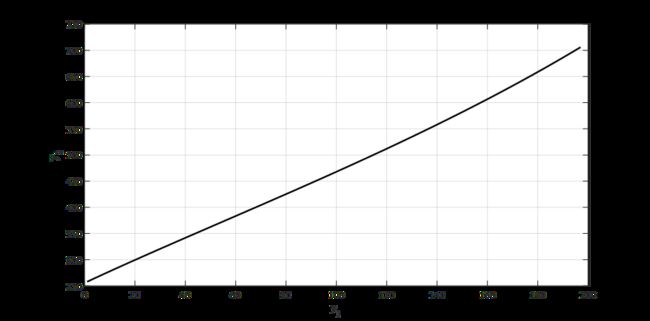
所以我们需要求其反函数。而直接公式求解过于复杂,所以我们采用反向插值的方式,即先以y1为自变量得到一系列y2的值,再根据这组数据,以y2为自变量,y1为因变量进行插值,得到近似的反函数。
我们可以根据插值结果,也就是反函数得到反向映射的具体坐标关系,再通过双线性插值的方式得到最终消除径向误差的结果。