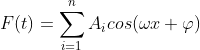同元Syslab使用攻略 | 信号分析基础-傅里叶变换原理简介及其应用
学习之前，先提出一个问题：“世界是复杂的还是简单的？”，相信绝大多数的人会不假思索地回答：世界肯定是复杂的。
在科研中，我们往往会用一些繁琐的数学公式来描述看似复杂的物理场景，但是我们深入思考一下，这些数学公式是不是都是由一些简单的物理原理组成呢？也就是说，其实我们的世界并不复杂，只是组成这个世界的简单物质之间形成了互相关联的关系。那么我们如何将这些相互关联的简单物质提取出来呢？这时候就可以使用非常经典的方法——傅里叶变换。
傅里叶变换是信号处理的基础算法。对复杂信号的处理和优化，可以使用傅里叶变换将复杂信号解析为易于分析的简单信号，这样处理复杂信号的问题就迎刃而解了。
01 时域与频域
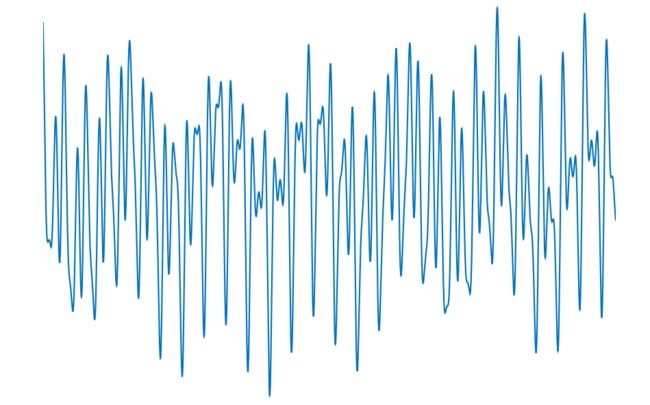
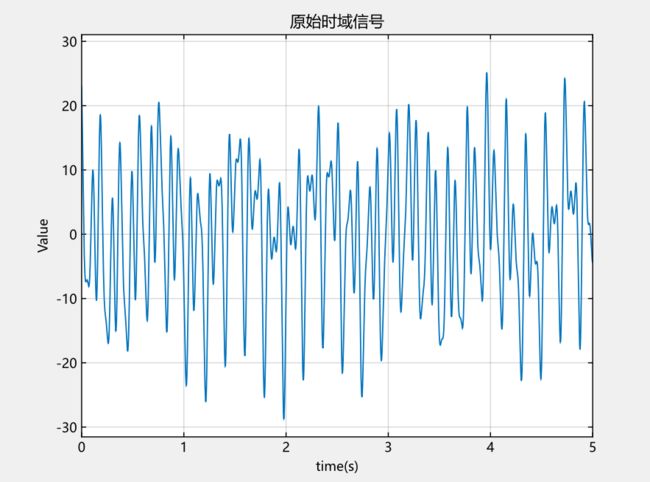
首先，让我们来看一张图：
本篇文章使用傅里叶变换将这个复杂信号进行解析。杂乱无章可能是大家看到这幅图的第一印象。这张图的横坐标轴是时间， 从出生到长大，我们都是以时间为参考来观察世界，这种方法称为时域分析。
我们再用一个简单的例子直观地理解什么是频域？
音波与五线谱
对于听众来说，音乐是一段音波，物体随时间震动产生声音，这是时域上的理解。但对于演奏者来说，音乐是五线谱上一个个音符，这是频域上的理解。上图为音乐分别在时域和频域上的不同表现形式。原来复杂的音波就是一个个简单音符的叠加。
其实早在18世纪，傅里叶就提出了：任意的周期函数都可以由一系列简单的正弦波进行线性组合，即：
02 傅里叶变换
傅里叶变换就是将信号从时域变换到频域。
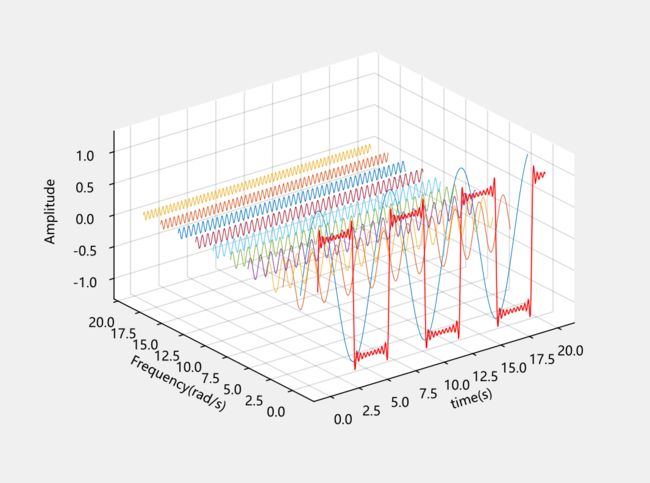
我们从三维视角来看复杂信号，即增加一个频率方向上的坐标轴，并将复杂信号根据频率分解为多个正弦波信号。
三维视角的复杂波
正弦波的标准表达式为y=Acos(ωx+φ)，我们只需要得到各个正弦波的频率、幅值和相位，即将复杂波的表达式采用多个正弦波表达式叠加的方式表示出来。
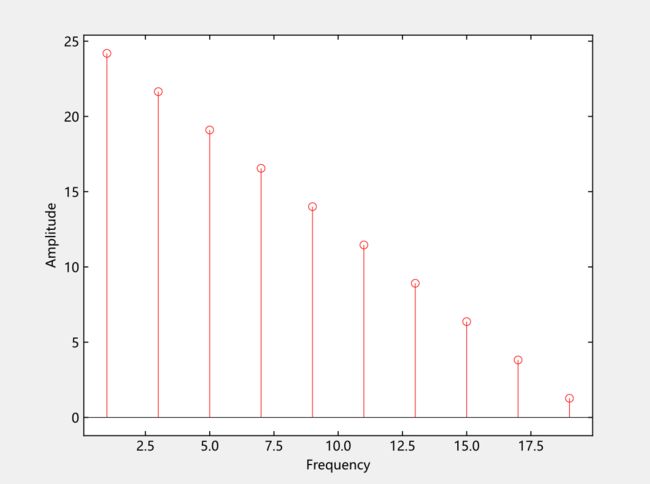
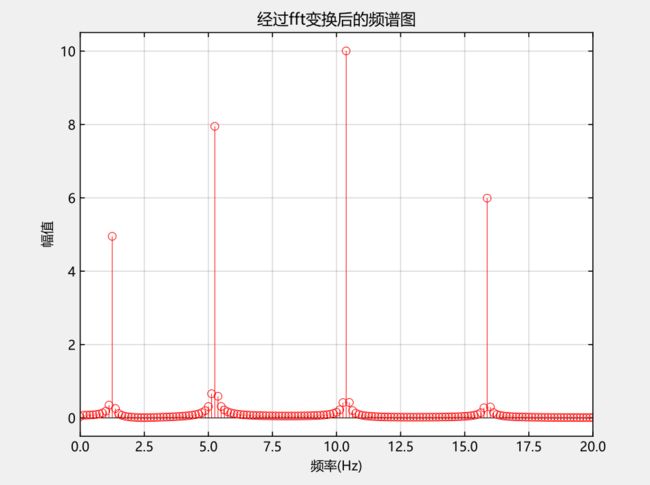
首先，我们从左向右观察这张三维视图，得到各个正弦波幅值与频率之间的关系，我们称为频谱，通过频谱来获取各个正弦波的幅值与频率。
频谱图
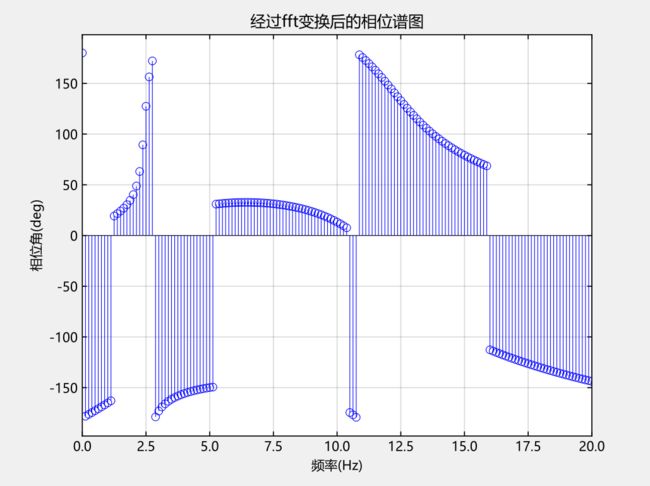
接下来，我们再以从上向下的视角来看，设定一个0相位的参考轴，相位谱就是用于描述各个正弦波相对于参考轴的相对位移。根据初中数学知识，即每一个正弦波的相位 
。这样，我们通过相位谱可以轻松获取各个正弦波的相位。
相位谱图
至此，我们获取了所有正弦波的频率、幅值和相位，可解析出复杂波的表达式。
03 傅里叶变换应用
傅里叶变换可以将复杂波分解为多个正弦波，这些正弦波的属性可以根据频谱和相位谱得到。接下来，我们将通过实例来讲解傅里叶变换如何在MWORKS.Syslab中获取复杂波频谱和相位谱，并将复杂波分解为多个简单的正弦波。
Syslab使用攻略 | 信号分析基础-傅里叶变换原理简介及其应用基于Syslab软件轻松使用傅里叶变换完成复杂信号解析
https://mp.weixin.qq.com/s/w1PIlN-qk64xVFwL2LRFkg
◎ 原始时域信号模拟
如上文所述，看似杂乱无章的波都是由若干个正弦波叠加而成。因此我们可以使用4个正弦波叠加模拟生成一个连续复杂波函数fun(x)，并通过广播的方式调用fun()函数，每隔1ms进行采样，得到原始信号数据。
#连续复杂波函数构建并采样fun(x) = 5cos(1.24 * 2π * x + π / 6) + 8cos(5.23 * 2π * x + pi / 4)+ 10cos(10.36 * 2π * x) + 6cos(15.85 * 2π * x + π / 3) #原始信号函数t_O = 0:1/1000:8 #采样步长1/1000，采样时间为8sy_O = fun.(t_O) #通过广播根据采样时间生成信号N_O = length(t_O) #原始采样点个数
使用Syslab软件中的plot函数绘制出复杂波在时域上的波形图，即原始时域信号图。
#绘制原始信号图figure() #创建图窗窗口plot(t_O, y_O, linewidth = 1) #绘制t_0与y_0相关的二维线图，且线宽为1磅grid("on") #显示坐标区网格xlim([0, 5]) #设置x轴的显示范围为[0,5]xlabel("time(s)") #横坐标标签为time(s)ylabel("Value") #纵坐标标签为Valuetitle("原始时域信号") #图名为原始时域信号
原始时域信号图
◎ 傅里叶变换
在Syslab软件中使用傅里叶变换将时域中的复杂波，在频域中展现其特性。具体操作如下：
1.原始信号采样
首先，对原始时域信号进行信号采样。信号采样需确定对应的采样频率，根据采样定理，采样频率应该大于信号频率的2倍以上，因此选用采样频率为64。根据采样频率计算出采样区间、采样点数和频率分辨率，通过采样分辨率计算出频域中的频率分布。最后通过对原始信号采样数据进行线性插值，并根据采样区间得到我们需要进行傅里叶变换的采样点。
#原始信号采样Fs = 64 # 信号采样频率,根据采样定理，信号采样频率应大于信号频率的2倍以上t = range(0, 8, length = 8Fs + 1) #采样点区间N = length(t) - 1 # 采样点数df = Fs / N #频率分辨率f = df * (0:N-1) #频域中的频率分布y1 = CubicSplineInterpolation(t_O, y_O, extrapolation_bc = Line()) #原始信号数据线性插值y2 = y1(t) #得到需要进行傅里叶变换的采样点
2.计算傅里叶变化
通过Julia语言提供的傅里叶变换函数fft()计算傅里叶变换。
#计算傅里叶变化YFFT = fft(y2)
3.计算单侧频谱幅值和相位
使用广播的方式计算傅里叶变换结果YFFT的双侧频谱幅值mag和相位phase，再基于mag和偶数信号长度N计算单侧频谱幅值magy。
#计算单侧频谱幅值和相位mag = abs.(YFFT) # 获取原始幅值phase = angle.(YFFT) * 180 / pi #获取相位角magy = mag / Nmagy = magy[1:Int(N / 2 + 1)]magy [2:end-1] = magy [2:end-1] * 2 #获取单侧频谱幅值mag
4.绘制频谱图、相位谱图
得到频域图和相位谱图所需要的绘图数据后，根据单侧频谱幅值magy和相位phase绘制出对应的频谱图和相位谱图。为了方便结果读取，我们采用stem函数进行针状图绘制。
#绘制频谱图figure()stem(f[1:Int(N / 2)], magy[1:Int(N / 2)], "r", markeredgecolor = "r", linewidth = 0.5)xlabel("频率(Hz)")ylabel("幅值")title("经过fft变换后的频谱图")grid("on")xlim([0, 20])
经过fft变换后的频谱图
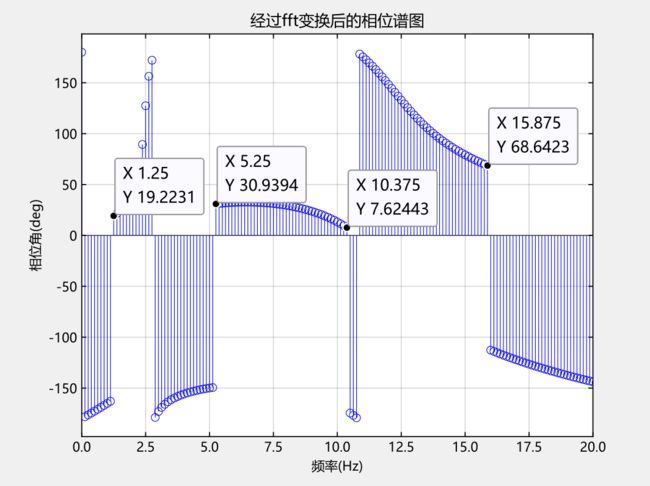
#绘制相位谱图figure()stem(f[1:Int(N / 2)], phase[1:Int(N / 2)], "r", markeredgecolor = "r", linewidth = 0.5)grid("on")xlim([0, 20])xlabel("频率(Hz)")ylabel("相位角(deg)")title("经过fft变换后的相位谱图")
经过fft变换后的相位谱图
◎ 信号重构
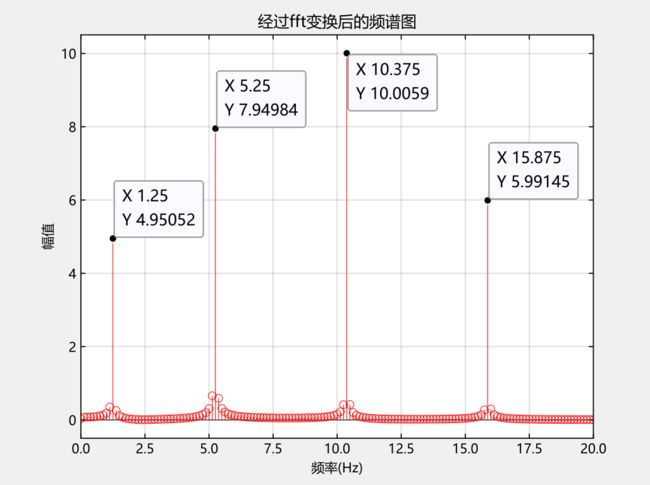
获取频谱图和相位谱图后，使用Syslab软件获取组成的正弦波的频率、幅值和相位。
获取频率和幅值
获取相位
根据各个正弦波的频率、幅值和相位得到各正弦波的表达式，并叠加得到复杂波表达式yfft。
# 获取复杂波表达式fo1(t) = 4.95cos(1.25 * 2π * t + (19.22 / 180 * π)fo2(t) = 7.95cos(5.25 * 2π * t + 30.94 / 180 * π)fo3(t) = 10.01cos(10.375 * 2π * t + 7.62 / 180 * π)fo4(t) = 5.99cos(15.875 * 2π * t + 68.64 / 180 * π)yfft = fo1.(t_O) + fo2.(t_O) + fo3.(t_O) + fo4.(t_O)
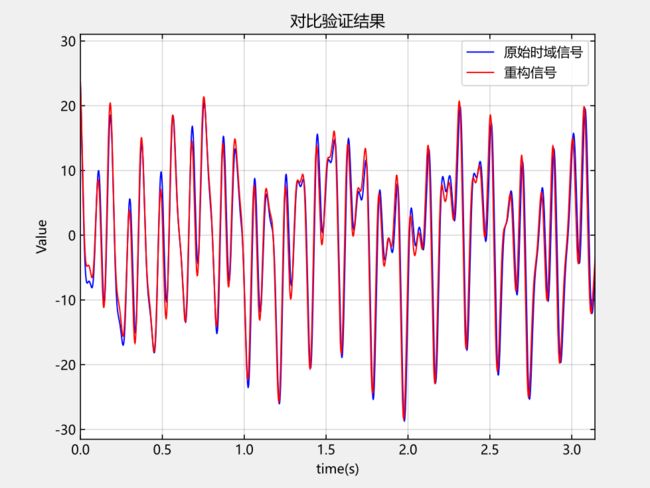
通过对原始复杂波和重构复杂波进行对比，查看原始信号和重构信号的拟合程度，验证其表达式的正确性。由下图可知，原始信号和重构信号拟合度非常高，因此可以认为重构的信号是准确的。
对比验证结果
04 思维拓展
根据傅里叶变换进行逆向思维，一个方波有没有可能由多个的简单的波叠加而成呢？
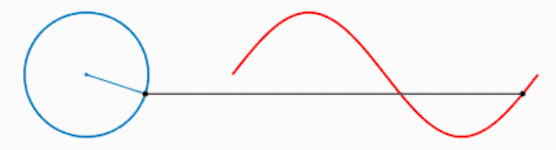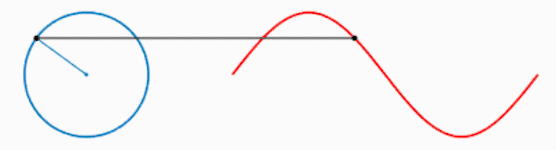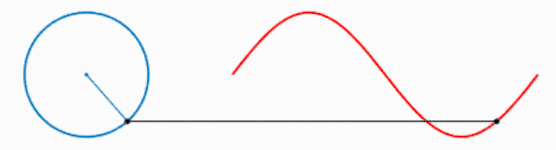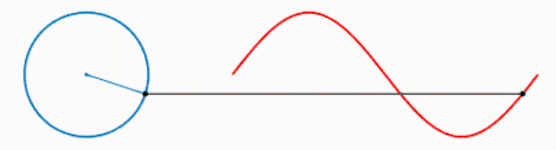
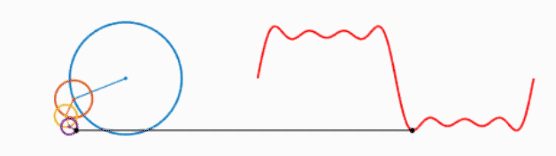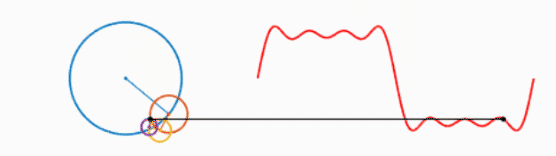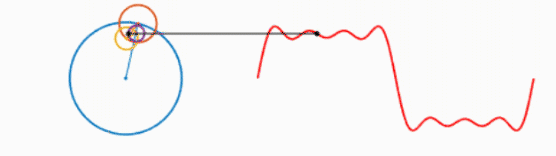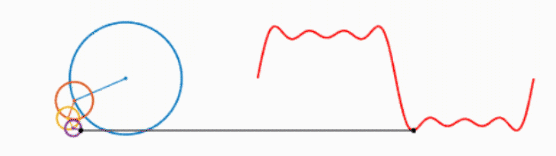
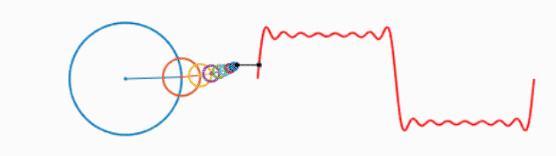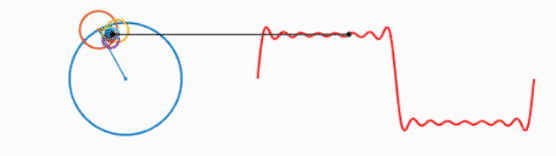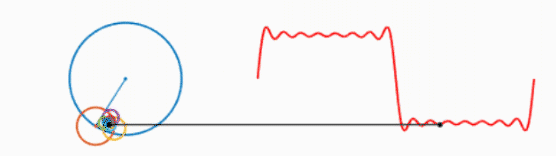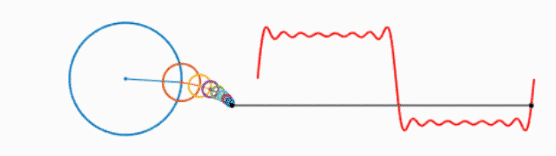
我们知道，一个圆不停地转动可以得到一个正弦波：
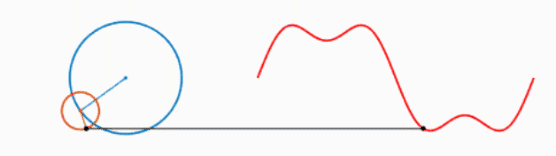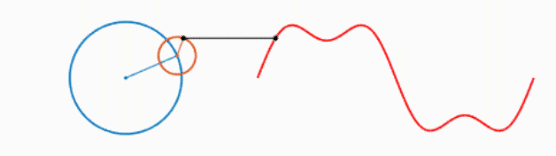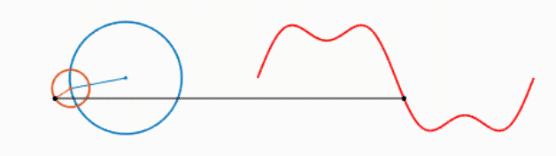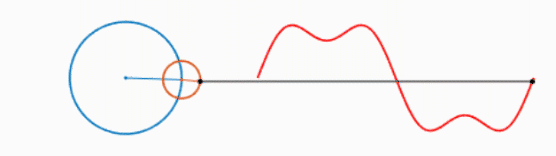
而多个正弦波的叠加可以表示为以下形式：
可以看出，叠加的信号越多，绘制的波形越接近方波。不妨大胆假设一下，当无限多的圆叠加，就可以绘制出方波，进而得出结论：方波可以由无数个正弦波叠加而成。
注：文章中的图片和动画（除音波和五线谱图）均使用MWORKS.Syslab生成。
MWORKS.Syslab作为新一代高级科学计算环境，可以高效解决科学与工程中遇到的矩阵运算、数值求解、数据分析、信号处理、控制算法设计优化、机器学习与并行计算等问题，实现基于模型对现代信息物理融合系统（CPS）开发的全流程支撑。同元软控为广大用户提供免费版本的MWORKS.Syslab，欢迎大家前往同元软控官网自行下载。
软件下载 - 苏州同元软控
https://www.tongyuan.cc/download