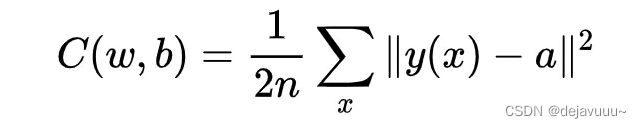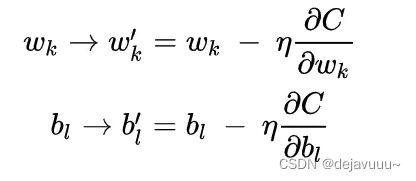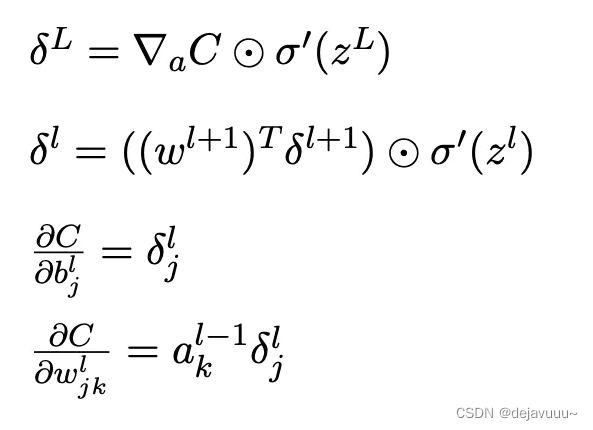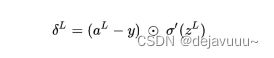全连接神经网络——MINST手写数字识别
简介
本文构建了一个全连接神经网络(FCN),实现对MINST数据集手写数字的识别,没有借助任何深度学习算法库,从原理上理解手写数字识别的全过程,包括反向传播,梯度下降等。最终的代码总行数不超过200行,并有详细的注释,很大程度上能够帮助理解。
我们假设已经了神经元相关的先验知识。
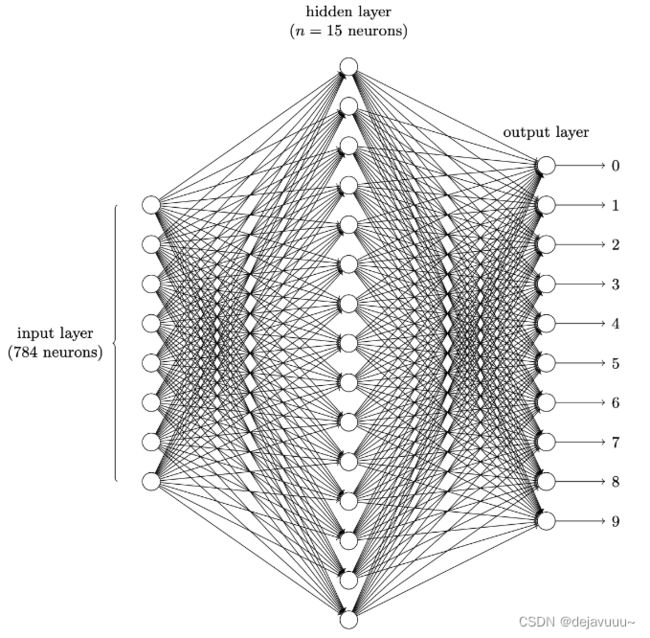
网络的结构如下,输入层一共28*28=784个神经元,隐藏层共15个神经元(这里可以自由设置),输出层一个十个神经元,分别代表十个数字(0~9)。
对于上图中的神经网络结构,假设我们随机初始化各个神经元的权值,并且将手写数字图片”9“传入到网络中,可以预见网络大概率并不会得到正确答案,但是我们可以通过不断调整权值来让它输出正确的结果。对于简单的模型也许这样做是可行的,因为毕竟可以调整的权重数据很少,但是对于我们定义的网络,它其中包含了784x15+15x10+15+10 = 11935个参数,手动修改就很不现实。
因此我们希望能够设计出一种学习算法,帮助我们自动调整感知器中的权重和偏置,以至于网络的输出能够拟合所有的训练输入。因此我们定义一个损失函数:
a代表的是神经网络的输出,y(x)代表的是输入x的标签。(前面的1/2是为了损失函数求导方便)
我们的目的,就是要最小化代价函数,代价函数越接近0,识别的效果就越好。
梯度下降
梯度下降的目的就是最小化代价函数。梯度表示的是各点处的函数值减小最多的方向,每次朝着梯度的方向,能够最大限度的减少函数的值。
因此,在寻找函数的最小值(或者尽可能小的值)的位置的任务中,要以梯度的信息为线索,决定前进的方向。在梯度法中,函数的取值从当前位置沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进,如此反复,不断地沿梯度方向前进。像这样,通过不断地沿梯度方向前进, 逐渐减小函数值的过程就是梯度法(gradient method)。
因此我们就有了下面这个更新w,b的式子。
其中![]() 为学习率。它的主要功能是用来控制每次变化的多少。如果太大,可能就会错过最低点;如果太小,每次变化的又太少,则需要花费很多的时间。因此选择一个合适的值非常重要。
为学习率。它的主要功能是用来控制每次变化的多少。如果太大,可能就会错过最低点;如果太小,每次变化的又太少,则需要花费很多的时间。因此选择一个合适的值非常重要。
随机梯度下降
注意到上面损失函数的形式,它是每个训练样本的损失函数值之和的平均,这就意味着我们需要遍历整个数据集,计算出每一个样本的梯度,这样导致一个问题:当训练集的数据很大时,训练的速度非常慢。
为了加速训练过程,在实际使用中,我们会采用随机梯度下降的算法。它的原理就是不采用整个数据集,而是随机选取小量训练样本来计算梯度,进而估算实际梯度。这部分数据我们叫做mini-batch。通过计算少量样本的平均值我们就可以快速得到一个对于实际梯度很好的估算,这有助于加速梯度下降,进而加快训练过程。
反向传播
先谈一谈反向传播和梯度下降的关系?
梯度下降法是一种优化算法,中心思想是沿着目标函数梯度的方向更新参数值以希望达到目标函数最小(或最大)。而这个算法中需要计算目标函数的梯度,那么反向传播就是计算梯度的一种方式。
反向传播的核心是对损失函数关于任何权重(或偏置)的偏导数的表达式。这个表达式告诉我们在改变权重和偏置时,损失函数变化的快慢。
反向传播基于4个基本方程,这些方程指明了计算误差![]() 和损失函数梯度的方法。先列举出来:
和损失函数梯度的方法。先列举出来:
其中第一个式子是由这个化来的,它表明了当前层L的误差的计算。
第二个式子是下一层(L+1)的误差和当前层(L)误差的关系
第三个式子则是损失函数关于偏置的变化率,即b的梯度
第四个式子则是损失函数关于权重的变化率,即w的梯度
(具体推导过程,请参考全连接神经网络之反向传播算法原理推导)
完整代码:
import random
import numpy as np
import mnist_loader
def sigmoid(z):
"""
Sigmoid激活函数
"""
return 1.0/(1.0 + np.exp(-z))
def sigmoid_prime(z):
"""
Sigmoid函数的导数
"""
return sigmoid(z)*(1-sigmoid(z))
class FCN(object):
"""
全连接网络
"""
def __init__(self, sizes):
"""
:param sizes: 是一个列表,其中包含了神经网络每一层的神经元的个数,列表的长度就是神经网络的层数。
如列表为[784,30,10],那么意味着它是一个3层的神经网络,第一层包含784个神经元,第二层30个,最后一层10个。
"""
self._num_layers = len(sizes)
# 生成偏置向量b,以[784,30,10]为例,生成2个偏置向量b,30x1,10x1
self._biases = [np.random.randn(y, 1) for y in sizes[1:]]
# 生成权重向量W, 生成2个权重向量w,30x784, 10x30
self._weights = [np.random.randn(y, x) for x,y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""
前向计算,返回神经网络的输出。公式如下:
output = sigmoid(w*x+b)
以[784,30,10]为例,权重向量大小分别为[30x784, 10x30],偏置向量大小分别为[30x1, 10x1]
a: 神经网络的输入,784x1.
"""
for b, w in zip(self._biases, self._weights):
a = sigmoid(np.dot(w, a) + b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None):
"""
使用小批量随机梯度下降来训练网络
:param epochs: 训练轮次
:param mini_batch_size: 小批量训练样本数据集大小
:param eta: 学习率
"""
if test_data: n_test = len(test_data)
print(n_test)
n = len(training_data)
for j in range(epochs):
# 在每一次迭代之前,都将训练数据集进行随机打乱,然后每次随机选取若干个小批量训练数据集
random.shuffle(training_data)
mini_batches = [training_data[k:k+mini_batch_size] for k in range(0, n, mini_batch_size)]
# 每次训练迭代周期中要使用完全部的小批量训练数据集
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
# 如果test_data被指定,那么在每一轮迭代完成之后,都对测试数据集进行评估,计算有多少样本被正确识别了
if test_data:
print("Epoch %d: accuracy rate: %.2f%%" % (j, self.evaluate(test_data)/n_test*100))
else:
print("Epoch {0} complete".format(j))
def update_mini_batch(self, mini_batch, eta):
"""
通过小批量随机梯度下降以及反向传播来更新神经网络的权重和偏置向量
"""
nabla_b = [np.zeros(b.shape) for b in self._biases]
nabla_w = [np.zeros(w.shape) for w in self._weights]
for x,y in mini_batch:
# 反向传播算法,运用链式法则求得对b和w的偏导
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
# 对小批量训练数据集中的每一个求得的偏导数进行累加
nabla_b = [nb + dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
# 使用梯度下降得出的规则来更新权重和偏置向量
self._weights = [w - (eta / len(mini_batch)) * nw
for w, nw in zip(self._weights, nabla_w)]
self._biases = [b - (eta / len(mini_batch)) * nb
for b, nb in zip(self._biases, nabla_b)]
def backprop(self, x, y):
"""
反向传播算法,计算损失对w和b的梯度
:param x: 训练数据x
:param y: 训练数据x对应的标签
"""
# 根据w,b大小初始化
nabla_b = [np.zeros(b.shape) for b in self._biases]
nabla_w = [np.zeros(w.shape) for w in self._weights]
# 前向传播计算网络的输出
activation = x
activations = [x]
zs = []
for b, w in zip(self._biases, self._weights):
# 利用公式z = w*x+b依次计算网络的输出
z = np.dot(w, activation) + b
zs.append(z)
activation = sigmoid(z) #pass the result z to activator function --> a = sigmoid(z)
# 将激活值存在列表中
activations.append(activation)
# 反向传播
# 首先计算输出层的误差
delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])
# 从输出层开始,计算损失函数对w,b的偏导数
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# 从倒数第二层开始,依次计算每一层的神经元偏导数
for l in range(2, self._num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
# 更新得到前一层的误差
delta = np.dot(self._weights[-l + 1].transpose(), delta) * sp
# 计算损失函数对w,b的偏导数
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l - 1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""
返回神经网络对测试数据test_data的预测结果,计算其中识别正确的个数
argmax函数返回激活值最大的神经元的下标(其实对应的就是数字本身)
"""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""
返回损失函数对激活值a的偏导数,损失函数定义 C = 1/2*||y(x)-a||^2
求导的结果为:
C' = y(x) - a
"""
return (output_activations - y)
if __name__ == "__main__":
# 获取MNIST训练数据集、验证数据集、测试数据集
training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
# 定义一个3层全连接网络,输入层有784个神经元,隐藏层30个神经元,输出层10个神经元
fc = FCN([784, 15, 10])
# 设置迭代次数30次,mini-batch大小为10,学习率为3,并且设置测试集,即每一轮训练完成之后,都对模型进行一次评估。
# 这里的参数可以根据实际情况进行修改
fc.SGD(training_data, 30, 10, 3.0, test_data=test_data)
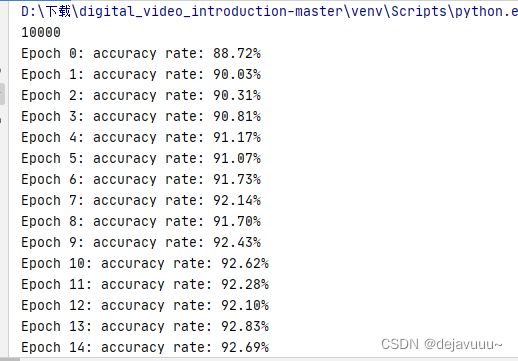
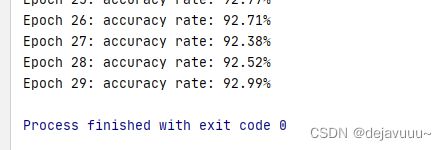
上述代码定义了一个3层的全连接神经网络,每层包含的神经元个数分别为784、30、10。epoch为30,小批量数据集个数为10,学习率为3.0。设置了测试数据集,每完成一个训练迭代周期之后,都会将测试数据集运用在神经网络上用来计算识别准确率,经过30次的迭代周期之后,最终达到了92.99%的识别正确率。