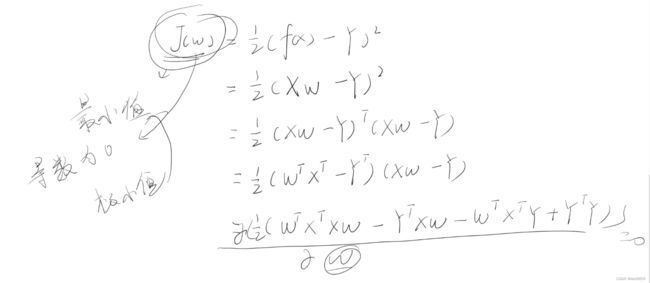深度学习入门
目录
- 1.线性回归
-
- 1.2 最小二乘法
- 1.2 梯度下降法
- 1.3 逻辑回归算法
- 2.全神经网络
-
- 2.1 全神经网络整体架构
- 2.2 激活函数的作用
- 2.3 激活函数
- 2.4 全神经网络前向传播
- 2.5 神经网络损失参数
- 2.6 链式法则
- 2.7 全神经网络反向传播
- 3.卷积神经网络
-
- 3.1卷积神经网络架构
- 3.2 卷积计算
- 3.2 填充操作
- 3.3 多通道卷积计算
- 3.4 池化运算
- 4.循环神经网络
-
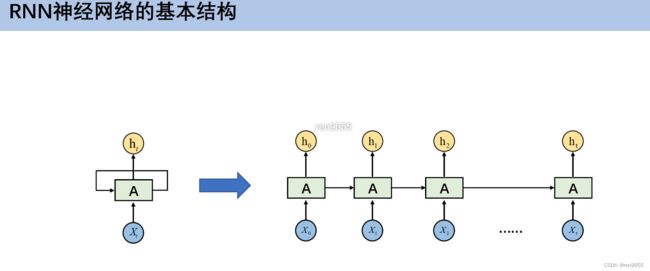
- 4.1 RNN基本结构
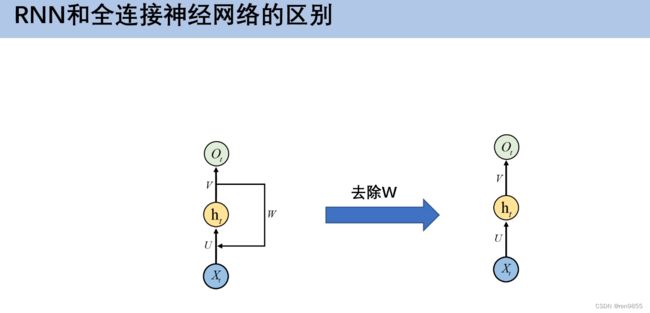
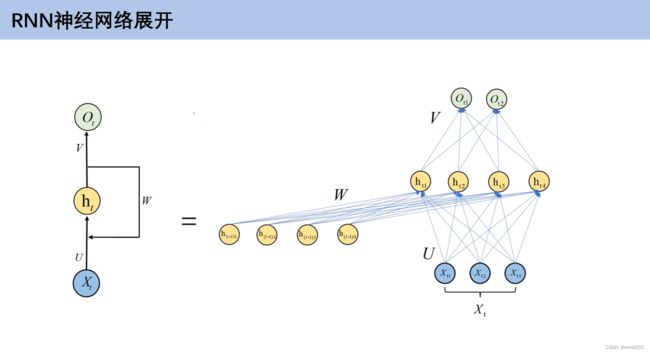
- 4.2 RNN与全连接神经网络的区别
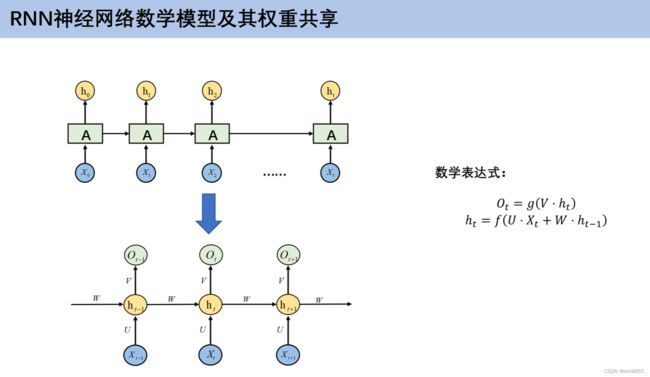
- 4.3 RNN数学模型
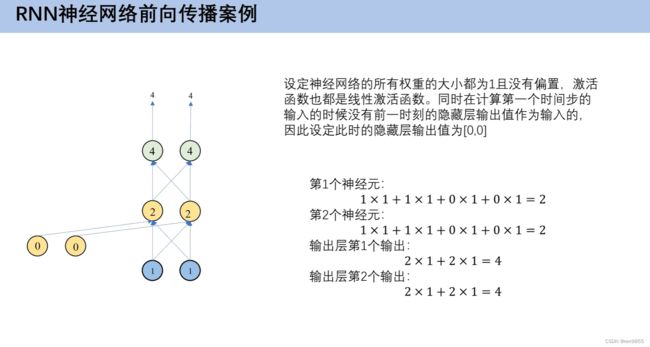
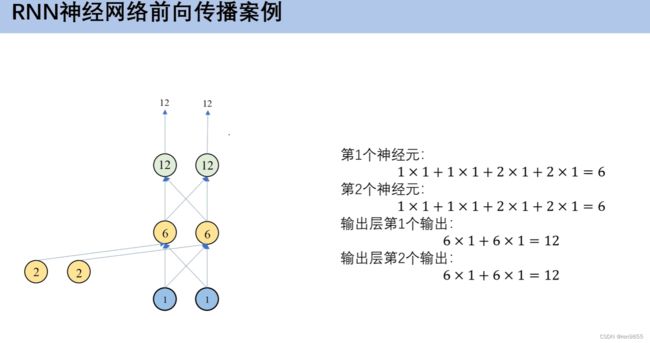
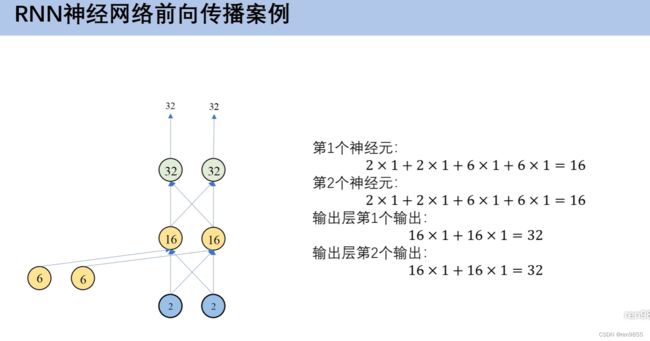
- 4.4 RNN神经网络前向传播
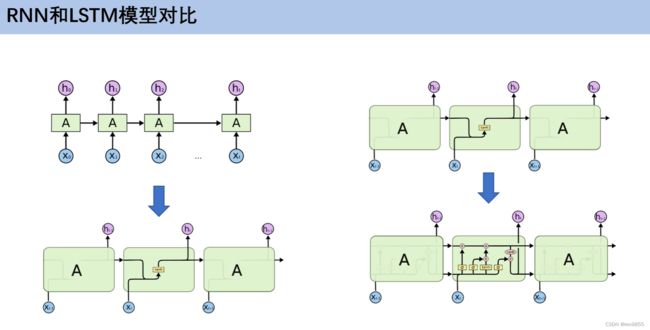
- 4.5 RNN和LSTM模型对比
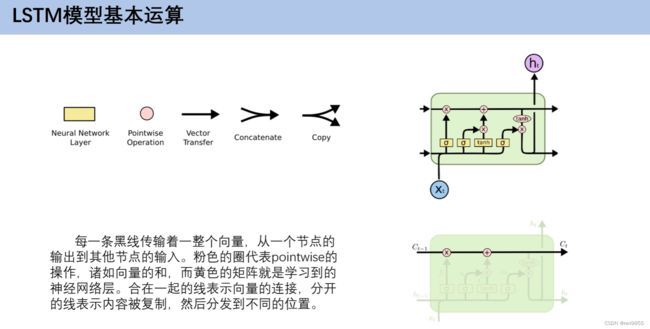
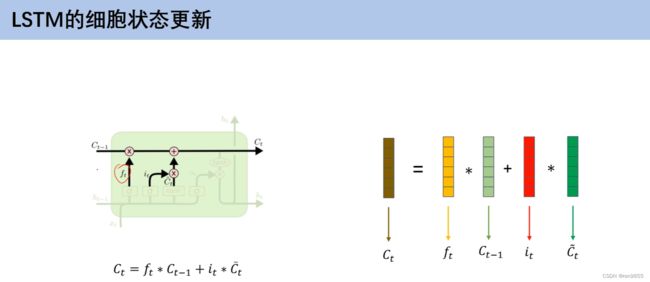
- 4.6 LSTM模型基本运算
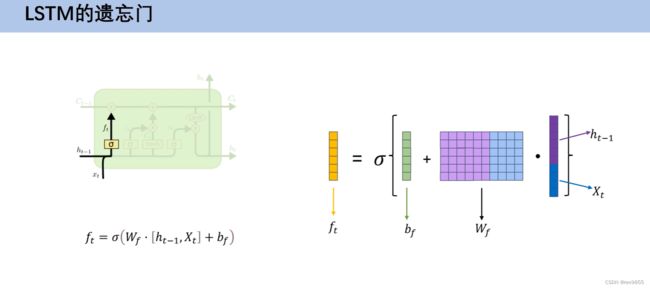
- 4.7 LSTM遗忘门
- 4.8 LSTM输入门
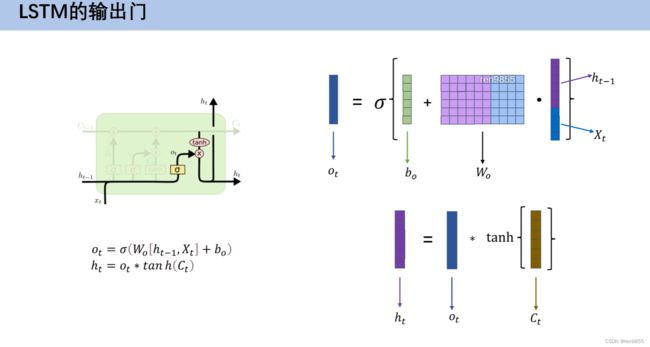
- 4.9 LSTM输出门
1.线性回归
假设给定数据集D={(x1,y1),(x2,y2),…,x是样本,y是特征,
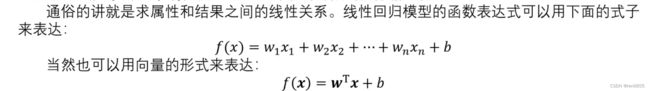
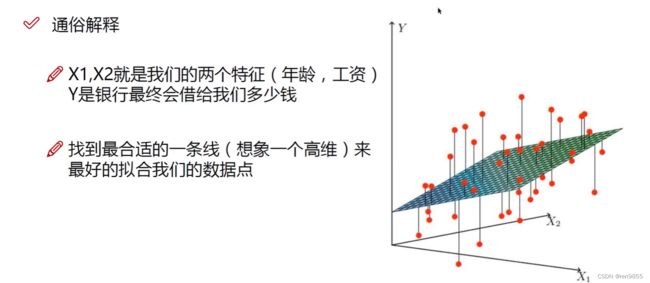
分类问题会有一个准确的值,回归问题就是会给一个区间,比如下图就是关于工资与年龄能够贷款多少钱的案例,我们要通过给定的x1,x2,y假定一个模型来判定给出其他x1,x2,得出的y值是否能很好的判断出来,我们假设模型是y=θ1x1+θ2x2,就要求出当前的θ1和θ2,

虽然我们的模型不能覆盖所有的点,但希望能覆盖尽可能多的点,所以我们找这一条线来拟合尽量多的点.
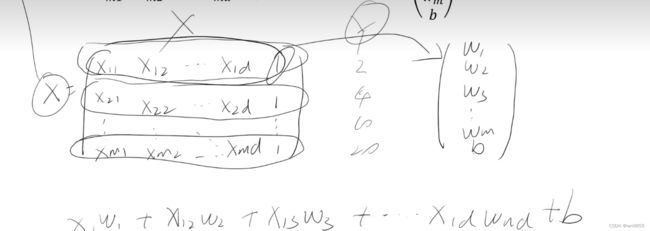
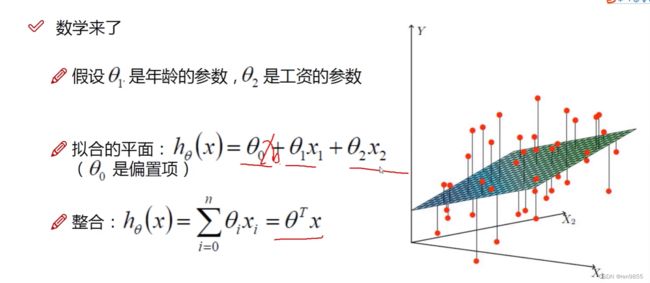
在 θ0后增添一项X0,让他们拼成一个矩阵,更好运算,如下图所示,
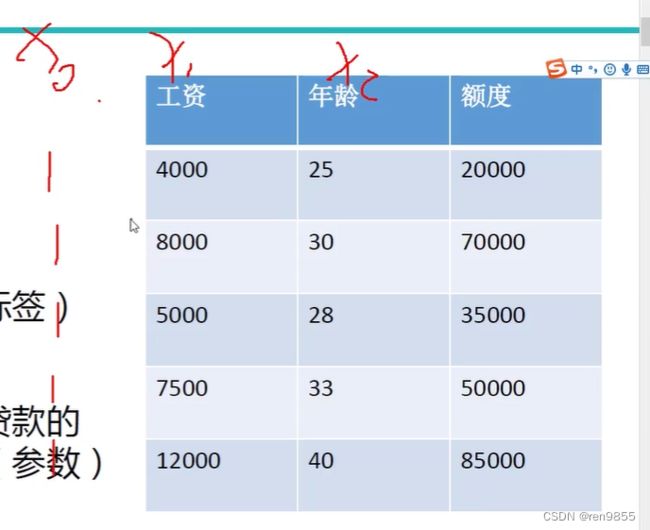
怎么样求解w和b来降低损失函数,提到了几个方法:
1.2 最小二乘法
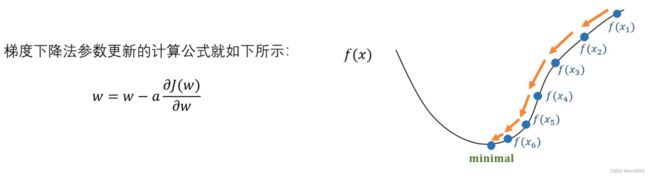
1.2 梯度下降法
1.3 逻辑回归算法
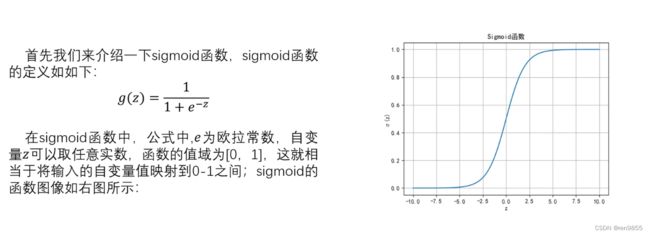
sigmoid函数值在(0,1)之间,将z转化为特征和权重的求和,将z替换,通过得出的值映射到概率上去,


2.全神经网络
2.1 全神经网络整体架构
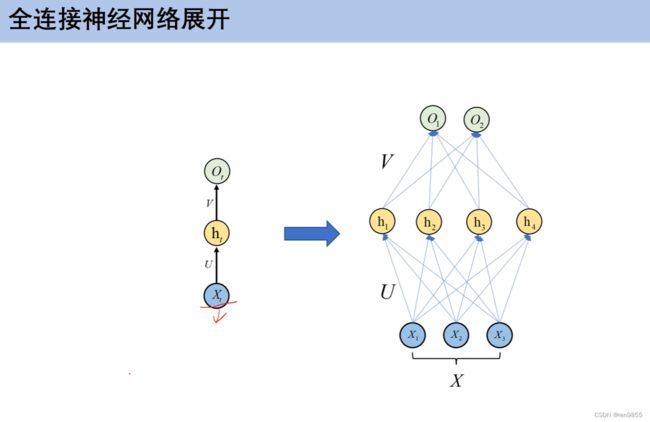
全连接神经网络是有输入层,隐藏层,输出层组成的,隐藏层在下图有2层,也可以有多层,就像他的名字一样,输入层的一个输入连接到隐藏层神经元的每一样点,隐藏层一层的点连接到隐藏层二层的每一个点,最后输出.
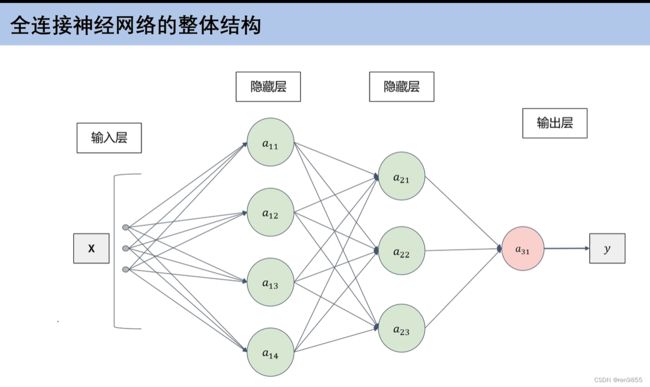
h是激活函数,是非线性的,在下图中如果多了激活函数,就是逻辑回归,没有逻辑函数,就变成了线性回归.
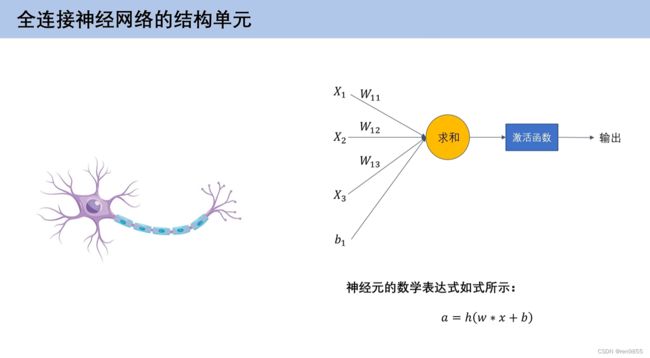
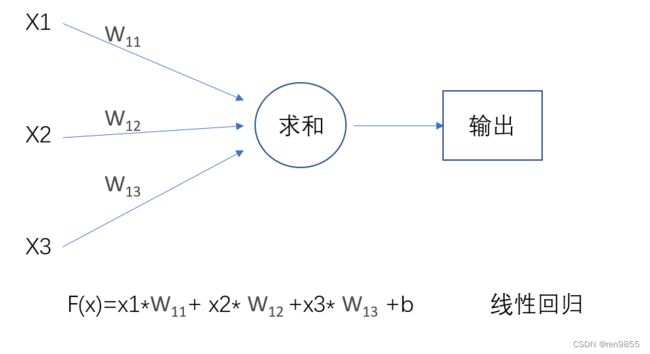
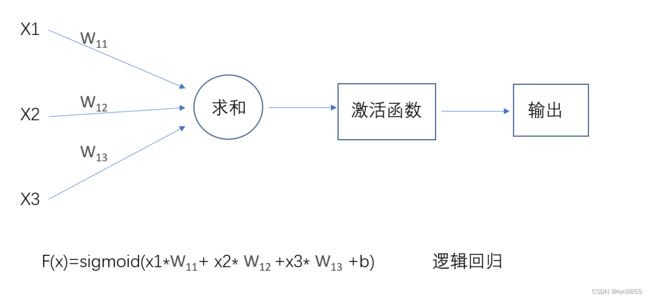
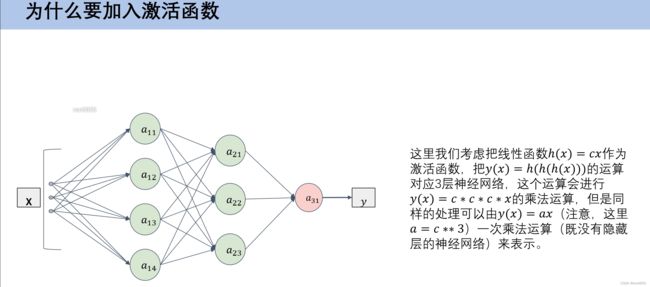
2.2 激活函数的作用
如果把激活函数设置成线性函数,最后得到的输出就是线性的,隐藏层的作用就没用了,所以要添加非线性的函数,当面对复杂问题可以更好计算.

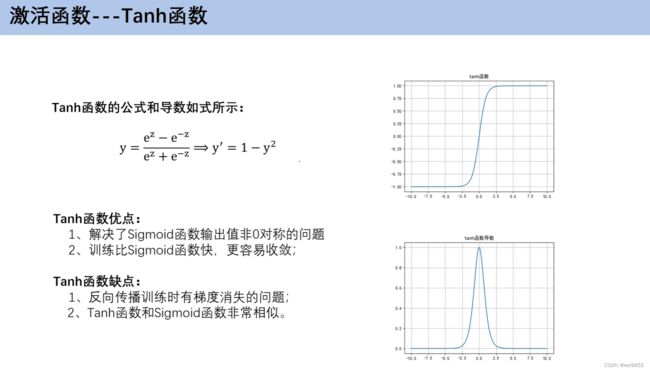
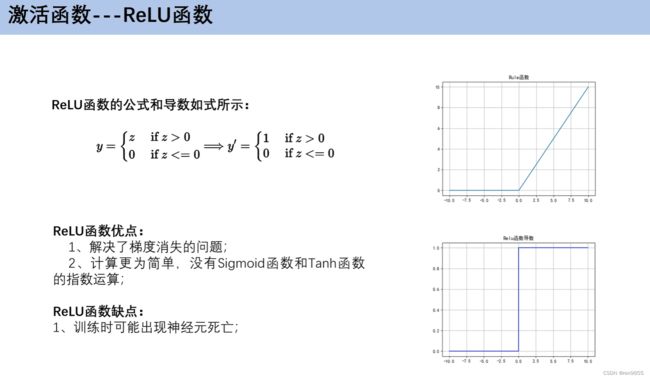
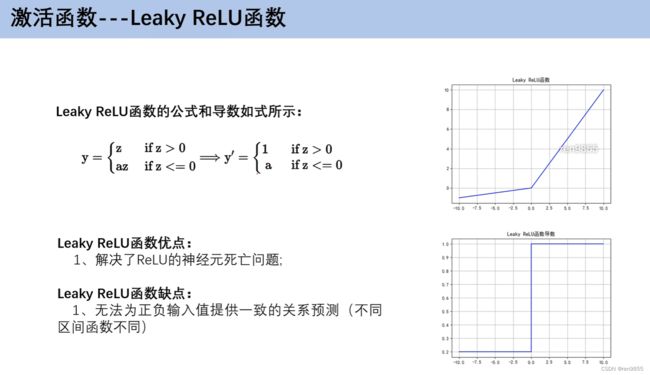
2.3 激活函数
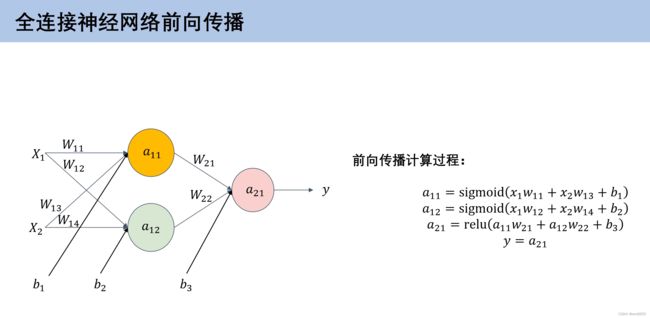
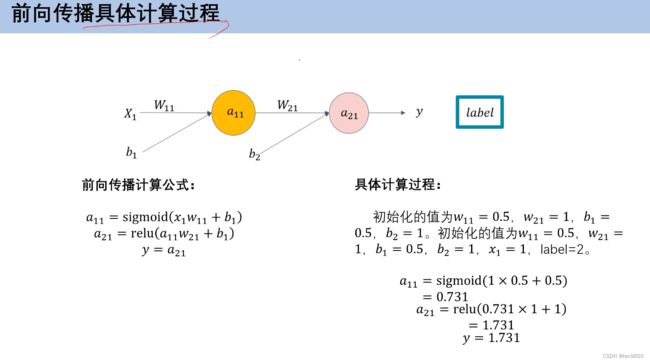
2.4 全神经网络前向传播
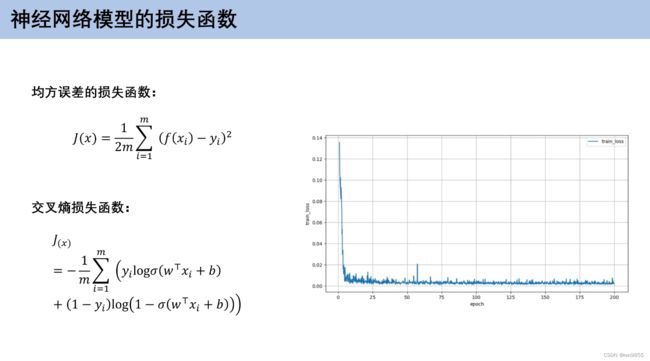
2.5 神经网络损失参数
2.6 链式法则
2.7 全神经网络反向传播
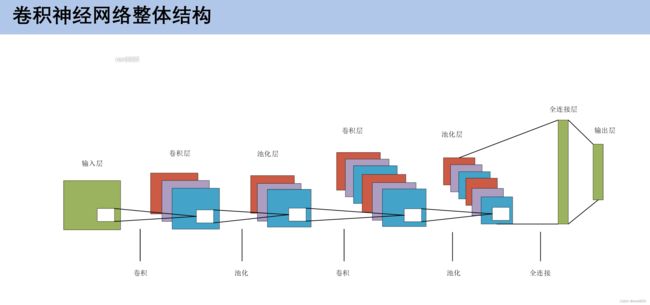
3.卷积神经网络
所谓三通道图像是指具有RGB三种通道的图像,简单来说就是彩色图像。R:红色,G:绿色,B:蓝色
单通道图,俗称灰度图,每个像素点只能有有一个值表示颜色,它的像素值在0到255之间,0是黑色,255是白色,中间值是一些不同等级的灰色
3.1卷积神经网络架构
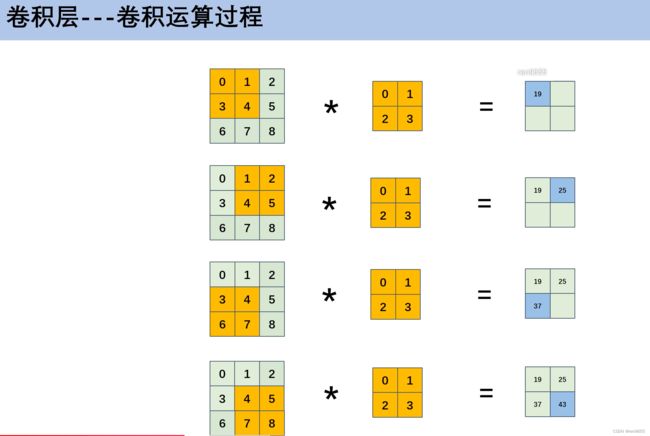
3.2 卷积计算
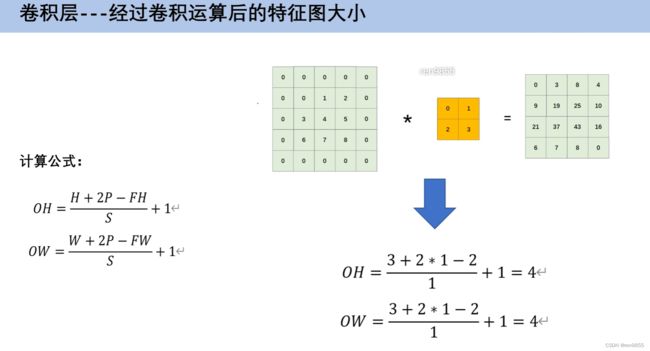
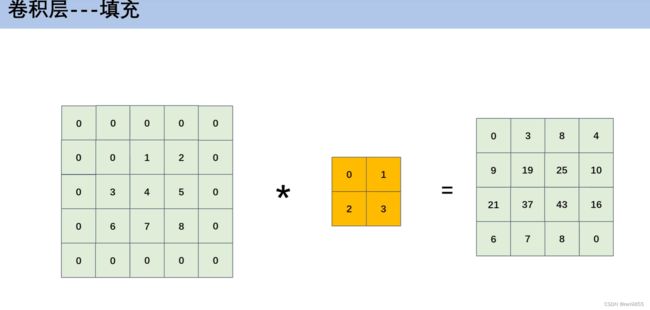
3.2 填充操作
通过填充输入数据,与卷积核相乘得到想要的输出大小
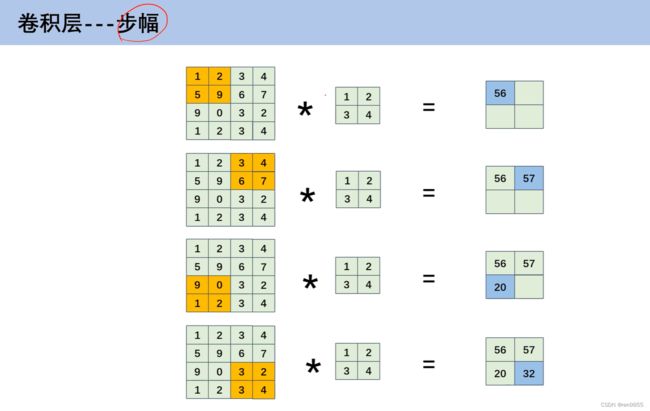
通过步幅去改变最后输出的大小
原先是33的输入,H是输入层的高度,P是向外填充的圈数,这里P向外填充了1圈,FH是卷积核高度,S是步幅,(3+21-2)/1+1=4,输入层高和宽是一样的,所以输出层大小跟上面算出来是一样的,都是4*4
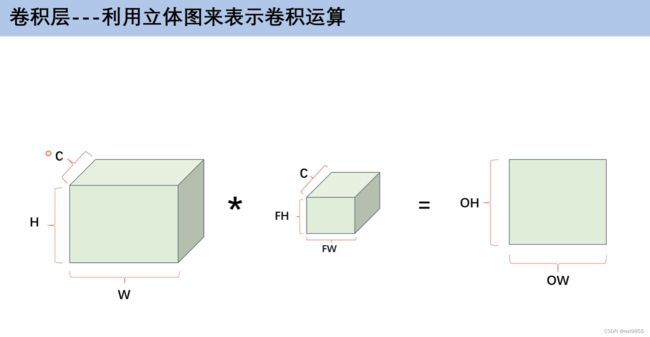
3.3 多通道卷积计算
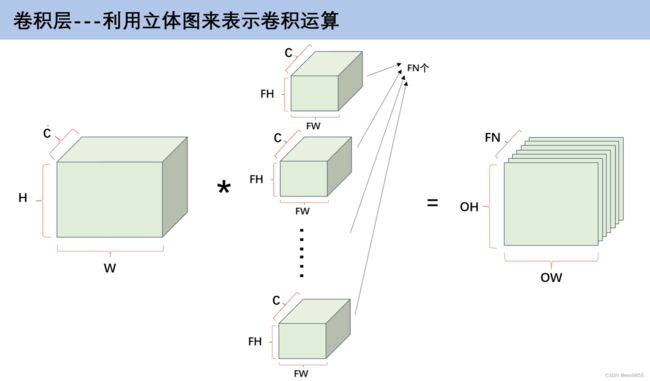
下图是3通道的图,对应的卷积核也是3通道的,第一个特征图与第一个卷积核计算,第二个特征图和第二个卷积核计算,第三个特征图和第三个卷积核计算,最后得出来的值加在一起.
![]()
C是通道为C的特征图
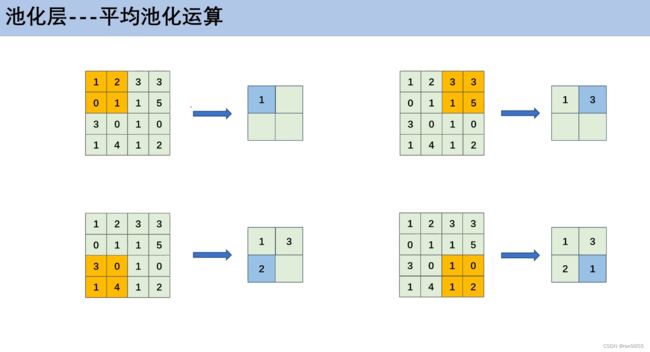
3.4 池化运算
最大化池化操作就是如下图所示,取出每个小块中最大的值
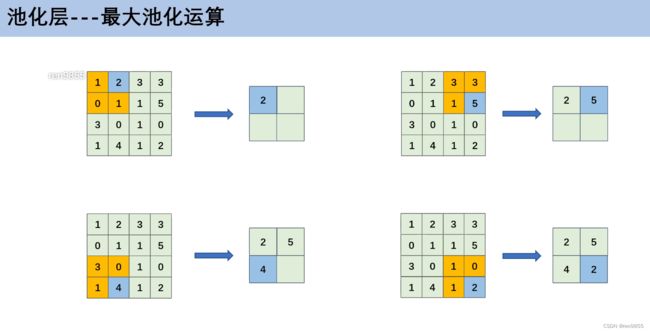
平均值池化是算平均值操作
(1+2+0+1)/4=1