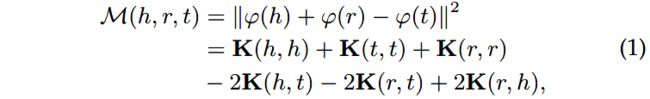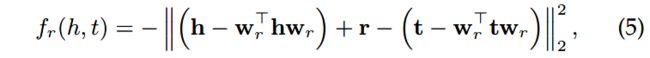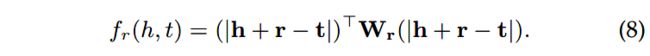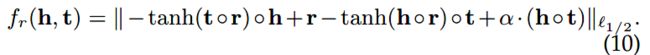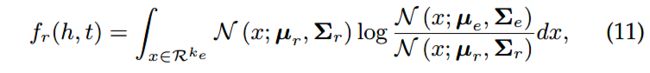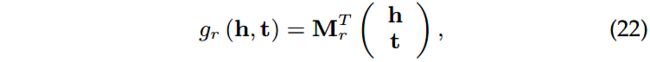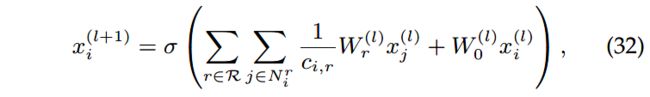【论文翻译 AAAI 2020 | 知识图谱综述】A Survey on Knowledge Graphs: Representation, Acquisition and Applications

论文题目：A Survey on Knowledge Graphs: Representation, Acquisition and Applications

论文来源：AAAI 2020 Philip S. Yu等人

关键词：知识图谱，表示学习，知识图谱补全，关系抽取，知识推理

待更新…
PS. 以后再也不翻译综述了，实在是太长了，也看不下去[捂脸哭泣]。
个人感觉这篇文章看一看每个小结的总结就行了，中间主要是方法的列举。
（都翻译了这么多，也不想接下来只翻译小结，还是善始善终吧）

---

---

1 摘要

知识图谱表示了实体间结构化的关系，已成为和认知与人工智能相关的热门的研究方向。

本篇综述介绍了知识图谱在不同领域的研究，包括：（1）知识图谱表示学习；（2）知识的获取和补全；（3）时序知识图谱：（4）知识感知的应用。本文还总结了近期的研究突破以及未来的研究方向。

知识图谱的嵌入考虑四个方面：表示空间、打分函数、编码模型和辅助信息。

对于知识的获取，尤其是知识补全、嵌入方法、路径推断和逻辑规则推理进行了综述。

本文还进一步探讨了一些新兴的主题，包括元关系学习、常识推理和时序知识图谱。

为了方便未来对知识图谱的研究，本文还提供了一个针对不同任务的数据集和开源库。

文章的最后分析了未来有前景的研究方向。

2 引言

（1）知识图谱（KG）的概念

人类知识的引入是AI的研究方向之一。知识表示和推理是为了给人工智能系统提供其可处理的知识，让其像人类一样具有解决复杂任务的能力。知识图谱可以以结构化的形式表示人类知识，近些年来在学术界和工业界均引起了广泛的关注。

知识图谱是事实（facts）、实体、关系以及语义描述的结构化表示。实体可以是真实世界中的物体，也可以是抽象的概念。关系表示了实体间的关系。关于实体和实体间关系的语义描述包含了预先定义好的类型和属性。属性图是广泛使用的一种图，图中的节点和关系有自己的属性。

---

（2）知识图谱（KG）与知识库（KB）

知识图谱和知识库大致上是近义词，但是有一点点区别。

当考虑图结构时，知识图谱可以视为一个图。当它涉及到形式语义（formal semantics）时，可以视为用于解释和推断事实的知识库。知识库和知识图谱的例子如图1所示：

知识库可以表示成资源描述符框架（RDF）下的事实三元组，例如三元组可以是$(head,relation,tail),(subject,predicate,object)$。也可以使用有向图进行表示，节点表示实体，边表示关系。

为了简化并顺应研究领域的趋势，本文将知识图谱和知识库同等看待。

---

（3）基于知识图谱的研究

1）知识图谱的表示学习

近期的基于知识图谱的研究关注于知识表示学习（KRL）或知识图谱的嵌入学习（KGE），主要思想是利用实体和关系的语义信息，将实体和关系映射成低维的向量表示。

2）知识的获取

知识的获取任务包括知识图谱的补全（KGC）、三元组分类、实体识别和关系抽取。

3）知识感知的模型

异质的信息、多语言的知识以及用于知识表示的丰富的实体和语义信息，有助于知识感知的模型。

因此，一些具有常识理解和推理的推荐系统、问答系统等获得了巨大的成功。例如微软的Satori和谷歌的知识图谱，在许多应用中表现出了强有效的服务能力。

---

（4）本文贡献

本文聚焦于知识表示，其使用更多的上下文（context）、智慧（intelligence）和语义信息来丰富图，以用于知识的获取和知识感知的应用。本文的主要贡献总结如下：

1）全面的阐述：

本文对知识图谱的起源和现代知识图谱关系学习技术进行了全面的综述。介绍并比较了主要的用于知识图谱表示学习和推理的神经模型。此外，还提供了不同领域中许多应用的完整概述。

2）全视角的分类以及新的分类标准

本文对知识图谱上的研究进行了全视角的分类，并提出了细粒度的新的分类标准。

我们从3个角度考虑知识图谱：知识图谱的表示学习（KRL）、知识的获取、知识感知的应用。

对于KRL的方法，作者进一步提出了细粒度的分类模式，一共有4类：表示空间、打分函数、编码模型以及辅助信息。

对于知识的获取，分为知识图谱的补全（KGC）、实体-关系的获取以及关系的抽取。1）针对KGC，从基于嵌入的排序、关系路径推理、逻辑规则推理以及元关系学习等方面进行综述；2）实体-关系的获取任务分为实体的识别、标注、消歧以及对齐；3）关系抽取根据神经范式（neural paradigms）进行讨论。

3）对最新研究进展的综述

知识图谱发展迅速，本文广泛涉及到了知识图谱的许多研究问题，包括基于transformer的知识编码、基于GNN的知识传播、基于强化学习的路径推理以及元关系学习。

4）总结并展望未来的研究方向

本文在每个分类都进行了总结，并突出强调了有前景的未来研究方向。

3 概览

3.1 简述知识库的发展历史

图结构知识表示的想法最早可以追溯到1956年由Richens提出的语义网的概念。symbolic logic knowledge可以追溯到1959年提出的General Problem Solver。

知识库一开始是用于基于知识的系统，解决推理任务或者其他问题。MYCIN最著名的基于规则的专家系统之一，使用有600条规则的知识库进行医学诊断。然后又有了基于框架的语言、基于规则的和混合表示的发展。在这一时期的最后，Cyc项目开始了，旨在汇集人类的知识。

之后资源描述框架（RDF）和Web本体语言（OWL）依次发布，成为语义网的重要标准。

接下来许多开放的知识库相继发布，例如WordNet、DBpedia、YAGO和Freebase。

Stokman和Vries在1988年提出结构知识图的新思想。然而，在2012年Google搜索引擎应用了知识图谱，才使得知识图谱得到了广泛的关注。

知识库历史的road map见附录A

3.2 定义和符号

将知识图谱定义成$\mathcal{G}=\{\mathcal{E},\mathcal{R},\mathcal{F}\}$，其中$\mathcal{E},\mathcal{R},\mathcal{F}$分别表示实体、关系和事实的集合。一个事实定义成三元组$(h,r,t)\in \mathcal{F}$。

一些符号和它们对应的描述如表1所示：

3.3 知识图谱上研究的分类

本文对知识图谱上的研究进行了综述，包括知识图谱表示学习、知识的获取以及下游的知识感知的任务。整体的分类如图2所示：

（1）知识表示学习（KRL）

KRL是知识获取和下游任务等的基础，我们将KRL分为4个角度：表示空间、打分函数、编码模型以及辅助信息：

1）表示空间指的是关系和实体将要被映射到的空间；

2）打分函数用于衡量事实三元组的合理性；

3）编码模型表示并学习到了关系间的交互；

4）辅助信息可合并到嵌入学习的方法中。

表示学习包括point-wise空间、流型（manifold）空间、复杂（complex）向量空间、高斯分布以及离散空间。

打分函数通常分为基于距离的和基于相似度匹配的函数。

目前的关于编码模型的研究工作主要有线性/双线性模型、基于分解的模型以及神经网络。

辅助信息包括文本的、视觉的和类型信息。

---

（2）知识的获取

知识的获取任务分为3类：

1）知识图谱的补全（KGC）：

用于扩展已有的知识图谱，还可分为以下几类：基于嵌入的排序、关系路径推理、基于规则的推理以及元关系学习。

2）关系抽取：发现新的关系知识，关系抽取模型有的利用了注意力机制、GCN、对抗训练、强化学习、深层残差学习（deep residual learning）以及迁移学习。

3）实体发现：发现新的实体知识，包括实体识别、实体消歧、实体分类和实体对齐。

---

（3）时序知识图谱

合并了时序知识用于表示学习，分为4类：1）时序嵌入；2）动态的实体；3）时序关系依赖；4）时序逻辑推理。

---

（4）知识感知的应用

包括自然语言理解（NLU）、问答、推荐系统和需要知识来提高表示学习能力的各种各样的应用。

3.4 相关的其他综述

有两个综述分别关注于KGE[1]和KRL[2]，和本文的工作最相关。

[1]使用线性的方式呈现KRL，侧重于定量分析。[2]根据打分函数对KRL方法进行了分类，并特别关注于KRL中使用到的信息的类型。

本篇综述从更深的角度阐述KRL，并且从4个角度提供了全方位的综述。而且本文还对知识获取和知识感知的应用进行了综述，涉及到了一些正在兴起的方向，例如基于知识库的推理、少样本学习等。

4 知识表示学习

知识表示学习（KRL）也可称为知识嵌入学习（KGE）、多关系学习和统计关系学习（SRL）。本节从4个角度介绍了最近的使用丰富的实体和关系中的语义信息进行分布的表示学习方法。

4.1 表示空间

表示学习的关键就是学习得到实体和关系的低维嵌入。现有的研究主要使用实值的point-wise地空间（如图 3a所示），包括向量、矩阵和张量空间，也有使用其他类型的空间例如复杂向量空间（图 3b）、高斯空间（图 3c）和Manifold space（图 3d）。

4.1.1 point-wise空间

point-wise欧式空间广泛用于实体和关系的表示，用于将关系嵌入映射到向量或矩阵空间或者捕获关系的交互信息。

TransE在$d$维的向量空间中表示实体和关系，例如$\mathbf{h},\mathbf{t},\mathbf{r}\in {\mathbb{R}}^d$，使得嵌入服从如下的转换规则：$\mathbf{h}+\mathbf{r}\approx \mathbf{t}$。

TranE方法是将实体和关系映射到同一个空间，TransR对其进行了改进，为实体和关系引入了分离的空间。作者通过映射矩阵$M_r\in {\mathbb{R}}^k$将实体（$\mathbf{h},\mathbf{t}\in {\mathbb{R}}^k$）映射到了关系（$\mathbf{r}\in {\mathbb{R}}^d$）所在的空间。

NTN[3]使用双线性张量神经层（bilinear tensor neural layer）跨多维对实体进行建模。

一些其他的translational models例如TransH也使用了相似的表示空间。语义匹配的模型使用了plain vector space（例如 HolE）和关系映射矩阵（例如 ANALOGY)。这些translational模型和语义匹配模型的规则将分别在4.2.1和4.2.2介绍。

4.1.2 复杂向量空间（Complex Vector Space）

不将实体和关系表示在实值的空间中，而是表示在一个复杂空间中，其中$\mathbf{h},\mathbf{t},\mathbf{r}\in {\mathbb{C}}^d$。以$\mathbf{h}$为例，它有实值部分$Re(\mathbf{h})$也有虚值部分$Im(\mathbf{h})$，$\mathbf{h}=Re(\mathbf{h})+iIm(\mathbf{h})$。

ComplEx首先引入了图 3b所示的复杂向量空间，可以捕获到对称的和反对称的关系。使用hermitian点乘来结合头实体和关系，以及尾实体的共轭。

受欧拉公式$e^{i\theta }=cos\theta +isin\theta$的启发，RotatE提出了一个旋转的模型（rotational model），将关系作为在complex space中从头实体到尾实体的rotation，例如$\mathbf{t}=\mathbf{h}\circ \mathbf{r}$，其中的$\circ$表示element-wise的Hadmard乘积。

QuatE使用一个带有3个虚部的四元组$Q=a+b\mathbf{i}+c\mathbf{j}+d\mathbf{k}$将complex-wise space扩展成hypercomplex $\mathbf{h},\mathbf{t},\mathbf{r}\in {\mathbb{H}}^d$。

4.1.3 高斯分布

受高斯词嵌入启发，基于密度的嵌入模型KG2E引入了高斯分布来处理确定的/不确定的实体和关系。作者将实体和关系嵌入到了一个多维度的高斯分布$\mathcal{H}\sim \mathcal{N}({\mu }_h,{\sum }_h)$和$\mathcal{T}\sim \mathcal{N}({\mu }_h,{\sum }_h)$中。均值向量$\mu$表示了实体和关系的位置，协方差矩阵$\sum$建模了它们的确定性/不确定性。根据转换（translational）的规则，实体转换的概率分布$\mathcal{H}-\mathcal{T}$定义为${\mathcal{P}}_e\sim \mathcal{N}({\mu }_h-{\mu }_t,{\sum }_h+{\sum }_t)$。

类似地，TransG使用高斯分布表示实体，使用混合的高斯分布表示关系嵌入，其中关系$r$的第$m$个部分的translation向量定义为${\mathbf{u}}_{r,m}=\mathbf{t}-\mathbf{h}\sim \mathcal{N}({\mathbf{u}}_t-{\mathbf{u}}_h,({\sigma }_h^2+{\sigma }_t^2)\mathbf{E})$。

4.1.4 Manifold and Group

这一小节介绍了知识在mainfold space, Lie group和dihedral（二面角） group（群）的表示。

mainfold（流形）是一个拓扑空间，可以定义成具有邻域的点的集合，group（群）是抽象代数中定义的代数结构。

之前的point-wise建模是不适定的代数系统，其中计分方程的数量远远超过实体和关系的数量。即使在某些子空间的投影方法中，嵌入也受到严格的几何形式的限制。

为了处理这一问题，MainfoldE将point-wise嵌入扩展成mainfold-based嵌入。作者引入了两种mainfold-based嵌入的设置，Sphere（球体）和Hyperplane（超平面）。例如图 3d所示，对于球体的设置，再生希尔伯特核空间（Reproducing Kernel Hilbert Space）用于表示mainfold函数，例如：

其中$\varphi$架构原始的空间映射到了Hilbert空间，$\mathbf{K}$是核函数。

另一个超平面的设置的引入通过交叉嵌入（intersected embeddings）增强了模型，例如：

TorusE通过在$n$维的compact Lie group（紧李群）torus（环面）空间进行嵌入解决了TransE的正则化问题。从向量空间到环面空间的映射定义为$\pi :{\mathbb{R}}^n\to T^n,x\mapsto [x]$，实体和关系定义为$[\mathbf{h}],[\mathbf{r}],[\mathbf{t}]\in {\mathbb{T}}^n$。类似于TransE，TorusE也在环面空间使用了关系的转换，例如$[\mathbf{h}]+[\mathbf{r}]\approx [\mathbf{t}]$。

近期提出的DihEdral模型，提出了保留2维多边形的二面体对称群（dihedral symmetry group）。

4.2 打分函数

打分函数可用于衡量事实的合理性，在基于能量的学习框架中也可认为是能量函数。

基于能量的学习旨在学习到能量函数${\mathcal{E}}_{\theta }(x)$，使得正样本得分高于负样本。

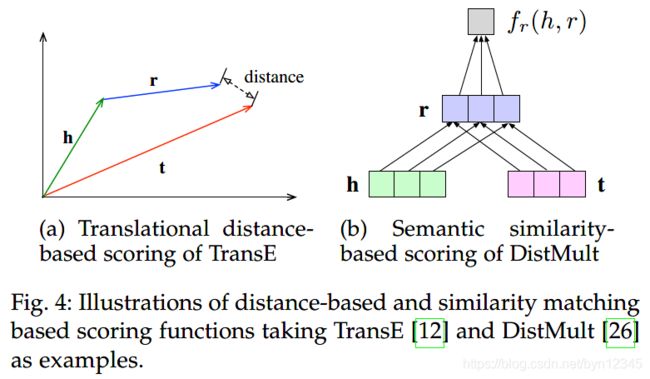
本文将打分函数分为两种类型：1）基于距离的，如图 4a所示；2）基于相似度的，如图 4b所示。

基于距离的打分函数通过计算实体间的距离，来衡量事实的合理性。其中关系的转换$\mathbf{h}+\mathbf{r}\approx \mathbf{t}$使用的最为广泛。

基于语义相似度的打分函数通过语义匹配来衡量事实的合理性，通常采用乘法的形式，例如${\mathbf{h}}^T{\mathbf{M}}_r\approx {\mathbf{t}}^T$，在表示空间中将头实体转换到和尾实体距离较近的地方。

4.2.1 基于距离的打分函数

主要思想是计算有关联的两个实体映射到表示空间的欧式距离。

（1）结构的嵌入（SE）使用两个投影矩阵和$L_1$距离来学习结构的嵌入：

（2）更广泛使用的是基于转换（translation）的打分函数，通过将关系看成是从头实体到尾实体的“翻译”来学习嵌入。

1）例如TransE方法就是假定$\mathbf{h}+\mathbf{r}$的嵌入应该和$\mathbf{t}$的嵌入接近，然后在$L_1$或$L_2$的约束下定义了打分函数：

2）此后诞生了许多TransE的变形和扩展。例如TransH将实体和关系映射到了超平面中：

3）TransR为实体和关系引入了分离的投影空间：

4）TransD构建了动态的映射矩阵${\mathbf{M}}_{rh}={\mathbf{r}}_p{\mathbf{h}}_p^T+\mathbf{I}$和${\mathbf{M}}_{rt}={\mathbf{r}}_p{\mathbf{t}}_p^T+\mathbf{I}$，其中${\mathbf{h}}_p,{\mathbf{t}}_p,{\mathbf{r}}_p\in {\mathbb{R}}^n$是投影向量，打分函数定义为：

5）TransA并没有使用欧式距离，而是使用马氏（Mahalanobis）距离来实现更有适应能力的度量学习，使用的打分函数定义如下：

6）之前的方法都是使用了附加的打分函数，TransF放松了translation的限制，使用点积的操作，例如$f_r(h,t)=(\mathbf{h}+\mathbf{r}{)}^T\mathbf{t}$。为了平衡在头实体和尾实体上的约束，使用了更宽松的translation打分函数，定义为：

7）最近提出的ITransF方法通过使用稀疏的注意力向量，学习到了关系和概念间的关联，实现了隐藏概念发现和统计强度转移（statistical strength transferring）。

8）TransAt整合了关系注意力机制和translational embedding。

9）TransMS使用非线性的函数和线性的偏置向量，传输了多个方向的语义信息，打分函数定义为：

10）使用高斯空间的KG2E和使用manifold的ManifoldE也使用了translational基于距离的打分函数。KG2E使用了两种打分方法：

第一种是非对称的KL散度：

第二种是对称的期望似然：

ManifoldE的打分函数定义为：

其中$\mathcal{M}$是manifold函数，$D_r$是特定关系的manifold参数。

4.2.2 语义匹配

另一个方向是计算语义相似性。

（1）SME对实体-关系对$(h,r)$和$(r,t)$进行语义匹配，匹配blocks-linear和bilinear block定义打分函数：

线性匹配block定义为$g_{left}(h,t)=M_{l,1}{h}^T+M_{l,2}{r}^T+b_l^T$，双线性形式为$g_{left}(h,t)=(M_{l,1}h)\circ (M_{l,2}r)+b_l^T$。

（2）通过限制关系矩阵$M_r$为对角矩阵，以用于多关系的表示学习，DisuMult提出了简化的双线性形式：

（3）为了捕获到关系数据中丰富的交互信息并且进行有效的计算，HolE引入了嵌入的循环相关（circular correlation of embedding），以学习到组合的表示。通过对循环相关与关系嵌入进行语义匹配，HolE的打分函数可定义为：

通过定义一个全息合成算子（a perturbed holographic compositional operator）$p(a,b;c)=(c\circ a)\ast b$，其中$c$是一个固定的向量，扩展的全息嵌入模型HolEx内插了HolE和全张量的乘积方法。给定$l$个向量$c_0,...,c_{l-1}$，HolEx的rank-l的语义匹配度量定义为：

（4）ANALOGY聚焦于多关系的推断，建模了关系数据的类比结构，打分函数定义为：

（5）CrossE引入了crossover interactions，使用了一个交互矩阵$C\in {\mathbb{R}}^{n_r\times d}$来模拟实体和关系的双向交互。通过在交互矩阵中查表得到特定关系的交互信息，例如$c_r=x_r^{T}C$。通过结合交互表示并匹配尾实体的嵌入，打分函数定义如下：

（6）语义匹配规则也可以使用神经网络进行编码，在第4.3节中有讨论。

（7）第4.1.4节中使用群表示的两个方法也遵循语义匹配规则。

TorusE的打分函数定义为：

通过将2L关系建模成group elements，DihEdral打分函数定义成多部分的和：

其中关系矩阵$\mathbf{R}$定义为块对角的形式，${\mathbf{R}}^{(l)}\in {\mathbb{D}}_K$，实体嵌入到实值空间中，${\mathbf{h}}^{(l)},{\mathbf{t}}^{(l)}\in {\mathbb{R}}^2$。

4.3 编码模型

本节介绍使用特定的模型结构，对实体间的交互信息以及关系进行编码的模型，包括线性/双新型模型、基于分解的模型以及神经网络。

线性模型通过将表示空间中的头实体投影到和尾实体相近的位置，将关系形式化为了线性/双线性的映射。

分解模型只在将关系数据分解成低秩的矩阵，以用于表示学习。

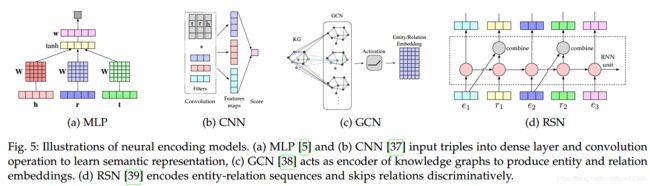
神经网络使用非线性激活函数编码关系数据并利用了复杂的神经网络结构。一些神经网络模型如图 5所示。

4.3.1 线性/双线性模型

这类模型通过应用线性操作，对实体间的交互以及关系信息进行编码，如下式所示。或者是像式（18）那样的双线性转换操作。

使用线性/双线性的方法包括SE, SME, DistMult, ComplEx, ANALOGY。

使用L2正则化的TransE，打分函数可以扩展成对一维向量的线性转换：

为了解决canonical Polyadia分解中实体向量的独立嵌入问题，SimplE引入了反向的关系并计算了$(h,r,t)$和$(t,r^{-1},h)$canonical Polyadia分数的平均值，如下式所示，其中$r^{{}^{\prime }}$是反向关系的嵌入：

4.3.2 分解模型

分解模型将KRL问题建模成了3个张量的分解。

张量分解的规则可以定义成：${\mathcal{X}}_{hrt}\approx {\mathbf{h}}^T{\mathbf{M}}_r\mathbf{t}$，分解函数遵循语义匹配的模式。

有学者提出RESCAL分解方法，在知识图谱张量的关系片（slice）上进行分解。对于$m$个关系中的第$k$个关系，$\mathcal{X}$的第$k$个slice被分解为：

作者进一步将其扩展以高效地处理实体的属性。有人提出了双线性结构的隐层因素模型（LFM），通过进行分解${\mathbf{R}}_k={\sum }_{i=1}^d{\alpha }_i^k{u}_i{v}_i^T$实现了对RESCAL的扩展。

通过引入three-way Tucker张量分解，TuckER通过输出核心的张量b并嵌入实体和关系，学习到了嵌入。其打分函数可定义为：

其中$\mathcal{W}\in {\mathbb{R}}^{d_e\times d_r\times d_e}$是Tucker分解的核张量，${\times }_n$表示张量按照第$n$个模式（mode）相乘。

4.3.3 神经网络

使用线性/双线性blocks的编码模型也可以使用神经网络进行建模，例如SME。

用于表示学习的神经模型包括多层感知机（MLP）、神经张量网络（NTN）和神经关联模型（NAM）。一般来说，这些方法将实体和关系输入到深层神经网络中，并计算语义匹配分数。

（1）MLP使用全连接层编码实体和关系，并使用带有非线性激活函数的第二层对三元组进行打分：

其中$\mathbf{W}\in {\mathbb{R}}^{n\times 3d}$是权重矩阵，$[h,r,t]$是三个向量的拼接。

（2）NTN将和关系张量相关联的实体嵌入作为输入，输出的预测打分为：

其中$b_r\in {\mathbb{R}}^k$是关系$r$的偏置，$M_{r,1},M_{r,2}$是特定关系的权重矩阵。可以视为是MLPs和双线性模型的结合。

（3）NAM将隐层编码和尾实体的嵌入相关联，并提出了relational-modulated的神经网络（RMNN）。

4.3.4 CNN

利用CNN来学习深层的表示特征。

（1）ConvE在嵌入上使用2D的卷积，并使用多层的非线性特征，通过将头实体和关系映射成2D的矩阵，来建模实体间和关系间的交互。例如${\mathbf{M}}_h\in {\mathbb{R}}^{d_w\times d_h}$和${\mathbf{M}}_r\in {\mathbb{R}}^{d_w\times d_h}$。打分函数定义为：

其中$w$是卷积核，$vec$是将tensor reshape成向量的向量化操作。

通过堆叠多层并进行非线性的特征学习，ConvE可以学习到语义级别的信息。

（2）ConvKB使用CNN编码实体和关系的拼接，并且不需要reshape，如图 5b所示。其打分函数定义为：

由卷积生成的一组特征图的拼接增强了潜在特征的学习能力。

（3）和捕获了局部关系的ConvE相比，ConvKB保持了过渡特性，表现出较好的实验性能。

（4）HypER使用了超网$\mathbf{H}$用于1D特定关系卷积核的生成，以实现多任务的知识共享，并且同时简化了2D的ConvE。可以看做是一个张量分解模型，将超网和权重矩阵看做张量。

4.3.5 RNN

之前的基于MLP和基于CNN的模型学习到了三元组级别的表示。为了捕获到KG中更长的关系依赖，可以使用基于RNN的方法。

（1）Gradner等人和Neelakantan等人提出基于RNN的模型，用于关系路径，分别在使用和不使用实体信息时，学习到向量表示。

（2）如图 5d所示的RSN，设计了循环skip机制，通过区分实体和关系，来增强语义表示学习。

包含实体和关系的关系路径例如$(x_1,x_2,...,x_T)$，是随机游走产生的，并且元素的位置和互换。然后使用其来计算循环隐层状态${\mathbf{h}}_t=tanh({\mathbf{W}}_h{\mathbf{h}}_{t-1}+{\mathbf{W}}_x{\mathbf{x}}_t+b)$。skip操作如下，其中${\mathbf{S}}_1,{\mathbf{S}}_2$是权重矩阵。

4.3.6 Transformers

基于transformer的模型促进了利用上下文本文的表示学习。

为了利用KG中的上下文信息，CoKE使用transformers来建模边和路径的序列。类似地，KG-BERT借鉴了语言模型的预训练思想并使用Transformer中的双向编码表示作为编码实体和关系的encoder。

4.3.7 GNN

图神经网络（GNN）是使用encoder-decoder框架学习结构的连通性。

（1）R-GCN提出了针对关系的转换来建模有向的KG，模型的前向传播定义成：

其中$x_i^{(l)}\in {\mathbb{R}}^{d^{(l)}}$是第$l$层第$i$个实体的隐层状态；$N_i^r$是和第$i$个实体有关系$r\in R$的邻居；$W_0^{(l)}$是可学习的参数矩阵；$c_{i,r}$是归一化，例如$c_{i,r}=|N_i^r|$。

GCN就是一个图编码器。为了针对特定的任务，编码器模型仍需要整合到R-GCN框架中。R-GCN平等对待每个实体的邻居。

（2）SACN引入了带权重的GCN，如图 5c所示，定义了有相同关系类型的两邻接节点的连接强度，利用节点结构、节点属性和关系类型，捕获KG中结构化的信息。

编码器模块Conv-TransE采用ConvE模型作为语义匹配的度量，并且保留了translation性质。

将实体和关系嵌入的卷积输出和$C$个核对齐为$\mathbf{M}(\mathbf{h},\mathbf{r})\in {\mathbb{R}}^{C\times d}$，打分函数定义为：

（3）Nathani等人引入使用多头注意力的图注意力网络，通过输入实体嵌入和关系嵌入的拼接，来捕获多跳的邻域特征。

4.4 使用辅助信息的嵌入

为了更有效地利用知识的表示，考虑使用多模态的嵌入作为外部信息，例如本文描述、类型限制、关系路径和视觉信息等。

4.4.1 文本描述

KG中有文本描述的实体定义为$\mathcal{D}=<w_1,w_2,...,w_n>$，作为语义信息的补充。

使用文本描述的KRL任务的挑战是将结构的知识和无结构的文本信息嵌入到同一个空间中。

（1）Wang等人提出了两个对齐的模型，通过引入实体名字和Wikipedia的锚（anchors），来对齐实体空间和单词空间。

（2）DKRL是TransE的扩展，该模型通过卷积编码器直接从实体描述中学习到了表示；

（3）SSP通过将三元组和文本描述投影到一个语义子空间，建模了三元组和文本描述间的强关联。

---

当将KGE任务和文本描述相联系时，通常会使用到联合的损失函数。

（1）上述的Wang等人使用的损失为$\mathcal{L}={\mathcal{L}}_K+{\mathcal{L}}_T+{\mathcal{L}}_A$，分别表示知识模型的损失、文本模型的损失以及对齐模型的损失。

（2）SSP的损失为$\mathcal{L}={\mathcal{L}}_{embed}+\mu {\mathcal{L}}_{topic}$，前者是针对嵌入的损失，后者是针对含有文本描述的topic的损失。

4.4.2 类型信息

使用层级的分类或者类型来表示实体，关系也可以有不同的语义类型。

（1）SSE合并了实体的语义类别，在语义空间中平滑地嵌入属于同一类别的实体。

（2）TKRL提出了实体投影矩阵的类型编码模型，以捕获类型层次结构。

（3）KR-EAR模型注意到了一些关系暗示着实体的属性，该模型将关系类型分类成属性和关系，并建模实体描述间的关联。

（4）Zhang等人使用关系簇、关系和子关系的层次关系结构，扩展了现有的嵌入方法。

4.4.3 视觉信息

视觉信息，例如实体的图片，可以丰富KRL。

IKRL模型包含了跨媒体的基于结构和基于图片的表示，将图片编码到实体空间，并且遵循translation规则。跨媒体的表示需要保证基于结构的和基于图片的表示在同一个表示空间中。

对于KRL人物，还有许多类型的辅助信息，例如属性、关系路径和逻辑规则。在第5.1.2节和第5.1.4节中将会讨论KGC任务下的关系路径和逻辑规则。

4.5 总结

知识表示学习（KRL）是知识图谱研究领域中一项很重要的研究。本节从4个角度介绍了KRL并列举了一些最近的方法，总结图表 2所示。

总之，提出新的KRL模型要回答以下4个问题：

1）应该选择什么样的表示空间；

2）如何衡量特定空间中的三元组的合理性；

3）选择什么样的编码模型对关系交互进行建模；

4）是否要利用辅助信息。

---

最流行的表示空间是欧式point-based空间，也就是将实体嵌入到向量空间中，并通过向量、矩阵或张量建模交互信息。

其他的表示空间包括复杂向量空间、高斯分布、manifold空间和群（group）。

1）Manifold空间和point-wise欧式空间相比的优点是放松了point-wise的嵌入。

2）高斯嵌入可以表达出实体和关系的不确定性，以及多种关系的语义信息。

3）复杂向量空间中的嵌入可以高效地建模不同的关系连接模式，尤其是对称/反对称的模式。

表示空间在编码实体的语义信息和捕获关系属性时发挥着重要的作用。当设计一个表示学习模型时，应该选择和编码模型在天然上相匹配的表示空间，并平衡表示和计算的复杂度。

使用基于距离度量的打分函数利用了translation规则，语义匹配的打分函数采用了组合运算符。

编码模型，尤其是神经网络模型，在建模实体和关系的交互信息时扮演了关键的角色。双线性模型也同样吸引了很多的注意力，一些张量分解的方法也可分为此类。

5 知识的获取

知识的获取目的是从非结构的文本中构建知识图谱，补全已有的知识图谱，并发现和识别实体和关系。

知识获取的主要任务包括关系抽取、KGC和其他的面向实体获取的任务，例如实体识别和实体对齐。

大多数方法将KGC和关系抽取问题分开处理。当然这两个任务也可以整合到一个框架中。Han等人提出了将知识图谱和文本数据融合的联合学习框架，解决了KGC问题和从文本中进行关系抽取的问题。

也有其他的和知识获取相关的工作，例如三元组分类和关系分类。本节从3个角度介绍知识获取的技术，包括KGC、实体发现和关系抽取。

5.1 知识图谱的补全（KGC）

KGC就是向知识图谱中添加新的三元组。典型的子任务包括链接预测、实体预测和关系预测。该任务可定义为：给定一个不完全的知识图谱$\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{F})$，KGC的目的是推断出缺失的三元组$\mathcal{T}=\{(h,r,t)|(h,r,t)\notin \mathcal{F}\}$。

对于KGC任务来说初级的研究关注于学习到低维的嵌入以用于三元组的预测，本文将这些方法称为基于嵌入的方法。

但是，其中的大多数方法不能捕获到多步的关系。因此最近的方法开始探究多步的关系路径，并利用逻辑规则，这类方法分别称为关系路径推断和基于规则的推理。

三元组分类是和KGC相关的任务，目的是评估一个事实三元组的正确性，本节也会进行额外介绍。

5.1.1 基于嵌入的方法

以实体预测为例，基于嵌入的排序方法如图 6a所示，首先基于现存的三元组学习到嵌入向量，然后将头实体/尾实体替换，来计算所有候选实体的得分，并进行排序得到top$k$个实体。

（1）之前提到的KRL方法，例如TransE、TransH、TransR、HolE和R-GCN，以及联合学习方法，例如DKRL，都可以用于KGC。

（2）PjoE方法并没有将输入和候选表示在同一的嵌入空间中，而是提出了组合的嵌入。具体表现为对输入三元组已知的部分进行空间投影（例如$(h,r,?),(?,r,t)$），以及有candidate-entity矩阵${\mathbf{W}}^c\in {\mathbb{R}}^{s\times d}$的候选实体，其中$s$是候选实体的数量。

嵌入映射函数包括一个神经组合层和一个输出映射层，定义为：$h(e,r)=g({\mathbf{W}}^c\sigma (e\oplus r)+b_p)$，其中$e\oplus r={\mathbf{D}}_{e}e+{\mathbf{D}}_{r}r+b_c$是对输入的实体-关系对进行组合的操作。

（3）之前提到的嵌入方法不能区分实体预测和关系预测，ProjE就不支持关系预测。因此，SENN就区分了3个KGC的子任务，具体方法是在同一的神经共享嵌入方法中，引入了带有自适应的权重的损失函数以学习不同的隐层特征。

（4）现有的方法高度依赖知识图谱中现存的连接，并且不能捕获到连接较少的事实知识或实体的演变。ConMask提出在实体描述上进行关系依赖的内容mask，以选择出和给定关系相关的片段（snippets），并提出基于CNN的目标融合来补全有不可见实体的知识图谱。

它只能在查询关系和实体明确地表示在了文本描述中时，进行预测。

（5）先前的方法是依赖于预先准备的实体对或文本语料的模型。对于医药领域，REMEDY提出了一个生成模型，称为条件关系变分自编码器，用于从潜在空间中发现实体对。

5.1.2 关系路径推理

实体和关系的嵌入学习虽然在一些任务中取得了不错的效果，但是不能对复杂的关系路径建模。关系路径推理利用了图结构中的路径信息。

（1）随机游走推断已经被广泛研究，例如Path-Ranking算法（PRA）在路径限制额组合下选择了关系路径，并且进行了极大似然分类。

（2）为了改进路径搜索，Gardner等人通过结合文本内容，在随机游走中引入了向量空间相似性的启发式方法，同时缓解了PRA中的特征稀疏性问题。

（3）Neelakantan等人提出了RNN模型，通过递归地应用组合性来组合关系路径的内涵，如图 6b所示。

（4）Chain-of-Reasoning是一种支持multiple reasons的神经注意力机制，它表示了跨所有关系、实体和文本的逻辑组合。

（5）最近，DIVA提出了统一的变分推断框架，该框架将多条推理视为两个子过程：1）路径的发现，底层路径推断的先验分布；2）路径推理，用于链接分类的似然。

5.1.3 基于强化学习的路径发现

深度强化学习（RL）通过将实体对间的路径发现问题形式化为序列决策问题，特别是马尔科夫决策过程（MDP），以实现多跳的推理。

policy-based RL智能体通过知识图谱环境间的相互作用，找到一个关系步骤，扩展推理路径，利用policy梯度来训练RL的智能体。

（1）DeepPath首先将RL应用在了关系路径学习上，并且提出了新的回报函数以提高准确率、路径多样性和路径高效性。DeepPath通过translational嵌入方法，在连续空间中编码状态，并将关系空间作为行动空间。

（2）类似地，MINERVA通过最大化期望回报，将走到正确答案实体的路径作为一个序列优化问题。

（3）Multi-Hop没有使用二元的回报函数，而是提出了soft回报机制。为了能够更有效地搜索路径，训练过程中还采用了action dropout来mask一些出边。

（4）M-Walk应用了RNN控制器来捕获历史的轨迹并使用蒙特卡洛树搜索（MCTS），以实现有效的路径生成。

（5）CPL通过利用文本语料和当前实体的sentence bag $b_{e_t}$，提出了用于从文本中进行路径发现和事实抽取的协同策略学习方法。

---

源实体、查询、当前实体分别表示为$e_s,e_q,e_t$，query relation定义为$r_q$，这些方法的MDP环境和policy networks总结在了表 3中，其中MINERVA, M-Walk, CPL使用的是二元的回报。对于policy networks，DeepPath使用了全连接网络，CPL的抽取器使用了CNN，其余的均使用了RNN。

5.1.4 基于规则的推理

为了更好地使用知识的天然符号特性，KGC的另一个研究方向是逻辑规则的学习。

（1）规则的定义

一个规则由head和body组成，形式化为$head\leftarrow body$。其中head是一个原子（atom），例如有着可变subject和/或objects的事实；body可以是原子的集合。例如给定关系$sonOf,hasChild,gender$，以及实体$X,Y$，有一个和逻辑编程相反的规则：

可以使用规则挖掘工具（例如 AMIE）来抽取出逻辑规则。最近的RLvLR提出了可扩展的规则挖掘方法，使用了高效的规则搜索和剪枝方法，并将抽取出的规则用于链接预测。

---

更多的研究关注于将逻辑规则整合到嵌入中，以提高模型的推理能力，例如使用联合学习和迭代训练用于合并一阶逻辑规则。

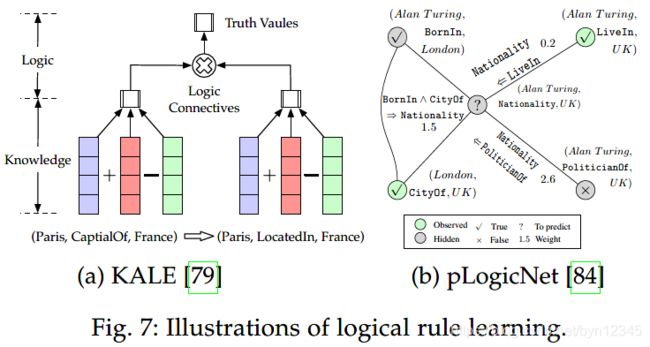
（1）KALE提出了统一的联合模型，定义了兼容三元组和逻辑规则嵌入的t-范数（t-norm）模糊逻辑连接词。定义了逻辑合取、析取和否定三种组合，构成complex formula的真值。图 7a展示了简单的一阶Horn clause推断。

（2）RUGE提出迭代的模型，使用soft rules从无标注的三元组进行soft的标签预测，从有标签的三元组进行embedding rectification。

（3）IterE提出递归的训练策略，有3个部分：嵌入学习；axiom induction；axiom injection。

---

神经模型和符号模型的结合同样吸引了研究者的注意力，其可使用端到端的方式实现基于规则的推理。

（1）Neural Theorem Provers (NTP) 学习到了用于多条推理的逻辑规则，利用了radial basis function kernel在向量空间上进行可微计算。

（2）NeuralLP实现了在归纳式的逻辑编程（inductive logic programming）中使用基于梯度的优化，其中的神经控制系统使用了集成注意力机制和辅助记忆。

（3）pLogicNet提出了概率逻辑神经网络，如图 7b所示，铜鼓结合Markov逻辑网络和KRL方法的优点，利用了一阶逻辑并学习到了有效的嵌入，同时处理了逻辑规则的不确定性。

（4）ExpressGNN[4]对graph networks和嵌入进行微调，对pLogicNet进行了泛化，并实现了更有效的逻辑推理。

参考文献

[1] Q. Wang, Z. Mao, B. Wang, and L. Guo, “Knowledge graph embedding: A survey of approaches and applications,” IEEE TKDE, vol. 29, no. 12, pp. 2724–2743, 2017.

[2] Y. Lin, X. Han, R. Xie, Z. Liu, and M. Sun, “Knowledge representation learning: A quantitative review,” arXiv preprint arXiv:1812.10901, 2018.

[3] R. Socher, D. Chen, C. D. Manning, and A. Ng, “Reasoning with neural tensor networks for knowledge base completion,” in NIPS, 2013, pp. 926–934.

[4] M. Qu and J. Tang, “Probabilistic logic neural networks for reasoning,” in NeurIPS, 2019, pp. 7710–7720.