用隐马尔可夫模型推测女朋友心情(Ⅴ):模型参数估计(模型训练)
上一期我们实现了训练样本的生成功能,这一期我们一起来讨论一下怎么用训练样本来估计模型参数,也就是解决隐马尔可夫模型的训练问题。上一期说过,我们用生成的训练样本来训练新模型的目的是想看看训练出的新模型的参数是否与原模型的参数几乎一致。也就是用测试驱动的方法验证一下模型算法是否正确。
1 初始状态概率向量参数的估计
根据初始状态概率向量的定义,第 i i i个元素表示初始状态为 s i s_i si的概率。于是,我们可以统计训练样本中首个时刻状态 s i s_i si出现的频次,计入元素 π i \pi_{i} πi,然后对向量进行归一化,最终得到初始状态概率向量的参数估计值,实现代码如下。
def estimate_pi(samples, max_state):
pi = [0] * max_state
for sample in samples:
pi[sample[0][0]] += 1
normalize_array(pi)
return pi
def normalize_array(arr):
sm = sum(arr)
for i in range(len(arr)):
arr[i] = arr[i]/sm
上述代码中,estimate_pi函数的入参samples是一个列表,列表中的元素为样本。每个样本是一个2行T列的二维列表。第0行为隐状态序列,第1行为观测序列,列长为T。max_state为隐状态个数,即模型共有多少个隐状态。
normalize_array()是归一化函数,其功能为对入参数组arr进行归一化。
2 转移概率矩阵参数的估计
记样本在 t t t时刻的状态为 s i s_{i} si,在 t + 1 t+1 t+1时刻为 s j s_{j} sj. 根据转移概率矩阵 A \boldsymbol A A的定义(详见第一期表-2),矩阵 A \boldsymbol A A第 i i i行元素表示从状态 s i s_{i} si转移到其它状态的概率。因此,我们需要统计样本序列中由状态 s i s_{i} si转移到状态 s j s_{j} sj的频次,将其计入转移概率矩阵 A i , j \boldsymbol A_{i,j} Ai,j,然后对第 i i i行归一化,就可得到由状态 s i s_{i} si转移到其它状态的概率分布,实现代码如下。
def estimate_transition_prob(samples, max_state):
A = [[0] * max_state for i in range(max_state)]
for sample in samples:
prev_s = sample[0][0]
for t in range(1, len(sample[0])):
s = sample[0][t]
A[prev_s][s] += 1
prev_s = s
for i in range(len(A)):
normalize_array(A[i])
return A
3 发射概率矩阵参数的估计
由第一期的表-3我们知道,发射概率矩阵的第 i i i行表示当状态为 s i s_{i} si时,观测值为 o j o_j oj的概率。所以,我们需要从训练样本中统计状态为 s i s_i si时,观测为 o j o_j oj的频次,计入矩阵元素 B i , j \boldsymbol B_{i,j} Bi,j,然后对矩阵第 i i i行进行归一化,得到状态为 s i s_i si时,出现各观测的概率分布。具体实现代码如下。
def estimate_emission_prob(samples, max_state, max_observ):
B = [[0] * max_observ for i in range(max_state)]
for sample in samples:
for t in range(len(sample[0])):
s = sample[0][t]
o = sample[1][t]
B[s][o] = B[s][o] + 1
for i in range(len(B)):
normalize_array(B[i])
return B
4 主调用函数代码
if __name__ == '__main__':
samples = generate(5, 10, 20000)
pi = estimate_pi(samples, 3)
A = estimate_transition_prob(samples, 3)
B = estimate_emission_prob(samples, 3, 4)
print("PI = ")
print(pi)
print("\nA = ")
for i in range(len(A)):
print(A[i])
print("\n B = ")
for i in range(len(A)):
print(B[i])
其中generate()是上一期实现的样本生成方法,上述代码用generate()生成20000个序列长度为5~10的样本。
5 程序运行截图
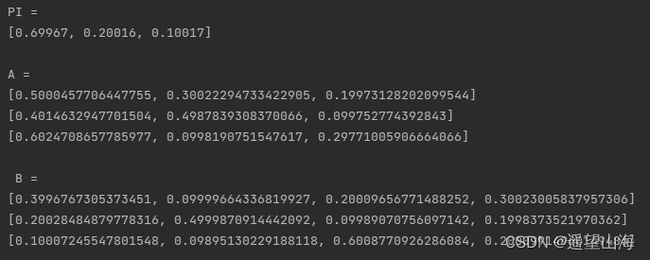
将运行结果与第一期中给出的 π \boldsymbol \pi π(表-1), A \boldsymbol A A(表-2), B \boldsymbol B B(表-3)做一下对比,我们可以看出,训练结果与原模型的参数几乎相等。
6 结束语
至此,关于“用隐马尔可夫模型推测女朋友心情”系列内容全部结束了。之所用推测女朋友心情这个例子,本意是想表达,我们可以用机器学习方法解决现实生活中许多有趣的问题。