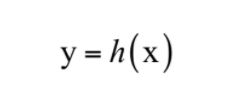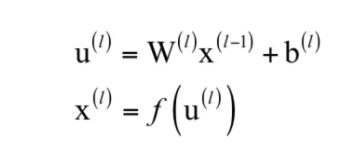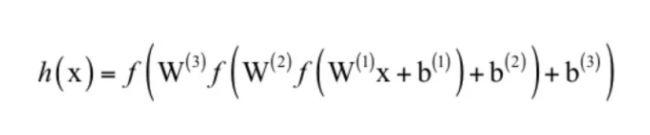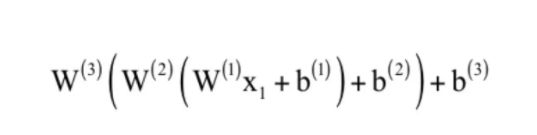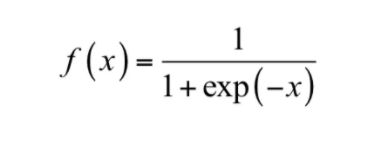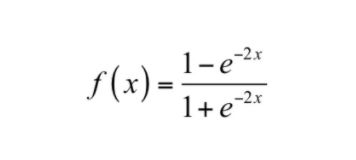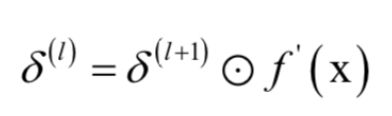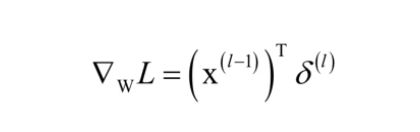神经网络基础02-激活函数+反向传播算法
参考文章:https://zhuanlan.zhihu.com/p/40903328
人工神经网络(Aritificial Neural Networks, ANN)
长短期记忆网络(LSTM,Long Short-Term Memory)
本文将由浅入深介绍循环神经网络RNN和长短期记忆网络LSTM的基本原理,并基于Pytorch实现一个简单应用例子,提供完整代码。
激活函数
为什么需要激活函数?
从数学上看,神经网络是一个多层复合函数。激活函数在很早以前就被引入,其作用是保证神经网络的非线性,因为线性函数无论怎样复合结果还是线性的。假设神经网络的输入是n维向量x,输出是m维向量y,它实现了如下向量到向量的映射:
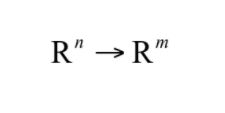
我们将这个函数记为:
除输入层之外,标准的前馈型神经网络第I层实现的变换可以分为线性组合、激活函数两步。在某些开源框架中,这两步可能会拆分成不同的层,以利于代码复用和灵活组合。例如Caffe(卷积神经网络框架)中线性组合由内积层InnerProductLayer类实现,激活函数由神经元层NeuronLayer类实现。神经网络第l层的变换写成矩阵和向量形式为:
其中W是权重矩阵,b是偏置向量,u是临时结果,x是神经网络每一层的输出。激活函数分别作用于向量u的每一个分量,产生一个向量输出x。在正向传播阶段,反复用上面的公式进行计算,最后得到网络的输出。对于一个3层的网络,整个映射可以写成:
这是一个3层的复合函数。从这里可以清晰的看到,如果没有激活函数,整个函数将是一个线性函数:
因此对激活函数最基本的要求是必须是非线性的。在早期,普遍使用的是sigmoid函数和tanh函数。sigmoid函数的计算公式为:
什么样的函数可以做激活函数?
什么样的函数是好的激活函数?
sigmoid函数的输出映射在(0,1)之间,单调连续,求导容易。但是由于其软饱和性,容易产生梯度消失,导致训练出现问题;另外它的输出并不是以0为中心的。
tanh函数的输出值以0为中心,位于(-1,+1)区间,相比sigmoid函数训练时收敛速度更快,但它还是饱和函数,存在梯度消失问题。
ReLU函数其形状为一条折线,当x<0时做截断处理。该函数在0点出不可导,如果忽略这一个点其导数为sgn。函数的导数计算很简单,而且由于在正半轴导数为1,有效的缓解了梯度消失问题。在ReLU的基础上又出现了各种新的激活函数,包括ELU、PReLU等。
激活函数总结
在工程实现时,如果将激活函数作为一个单独的层,则在正向传播时对输入向量的每个分量计算激活函数值f(x)。在反向传播时对输入数据计算导数值f’(x),然后乘以后一层送入的误差项,得到本层的误差项,送入前一层中:
反向传播算法推导
介绍
反向传播算法从多元复合函数求导的链式法则导出,递推的计算神经网络每一层参数的梯度值。算法名称中的“误差”是指损失函数对神经网络每一层临时输出值的梯度。
反向传播算法从神经网络的输出层开始,利用递推公式根据后一层的误差计算本层的误差,通过误差计算本层参数的梯度值,然后将差项传播到前一层。
反向传播算法是一个通用的思路。全连接神经网络(多层感知器模型,MLP)给出的是全连接层的反向传播实现;卷积神经网络(CNN)引入了卷积层和池化层,对这两种层的反向传播做了自己的处理;循环神经网络(RNN)因为在各个时刻共享了权重矩阵和偏置向量,因此需要进行特殊处理,为此出现了BPTT算法,误差项沿着时间轴反向传播。
本文推导全连接神经网络的反向传播算法。
链式法则
在正式介绍神经网络的原理之前,先回顾一下多元函数求导的链式法则。对于如下的多元复合函数:
在这里,x和y是自变量。其中u,v,w是x的函数,u,v是y的函数,而f又是u,v,w的函数。根据链式法则,函数f对x和y的偏导数分别为:
总结起来,函数自变量x的偏导数等于函数对它上一层的复合节点的偏导数(在这里是u,v,w)与这些节点对x的偏导数乘积之和。因此,我们要计算某一个自变量的偏导数,最直接的路径是找到它上一层的复合节点,根据这些节点的偏导数来计算。
神经网络原理简介
神经网络一般有多个层。第一层为输入层,对应输入向量,神经元的数量等于特征向量的维数,这个层不对数据进行处理,只是将输入向量送入下一层中进行计算。中间为隐含层,可能有多个。最后是输出层,神经元的数量等于要分类的类别数,输出层的输出值被用来做分类预测。
需要解决的一个核心问题是一旦神经网络的结构(即神经元层数,每层神经元数量)确定之后,怎样得到权重矩阵和偏置项。这些参数是通过训练得到的,这是之后推导的核心任务。
算法流程
什么样的函数能很好的解释这批训练样本?答案是神经网络的预测输出要尽可能的接近样本的标签值,即在训练集上最小化预测误差。
单个样本的反向传播算法在每次迭代时的流程为:

实现时需要在正向传播时记住每一层的输入向量x(l-1),本层的激活函数导数值![]()
。
神经网络的训练算法可以总结为:
复合函数求导+梯度下降法
训练算法有两个版本:批量模式和单样本模式。批量模式每次梯度下降法迭代时对所有样本计算损失函数值,计算出对这些样本的总误差,然后用梯度下降法更新参数;单样本模式是每次对一个样本进行前向传播,计算对该样本的误差,然后更新参数,它可以天然的支持增量学习,即动态的加入新的训练样本进行训练。
在数学中,向量一般是列向量,但在编程语言中,向量一般按行存储,即是行向量,因此实现时计算公式略有不同,需要进行转置。正向传播时的计算公式为:

这些向量都是行向量。