python线性回归实现波士顿房价预测

线性回归

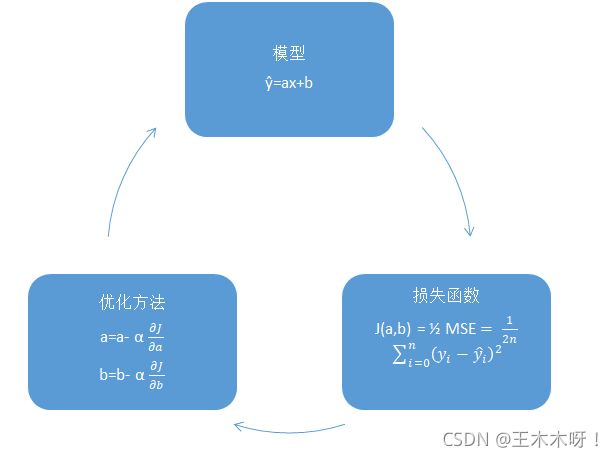
线性回归属于机器学习中的一种，机器学习就是机器可以自己学习，而机器学习的方法就是利用现有的数据和算法，解出算法的参数。从而得到可以用的模型。监督学习就是利用已有的数据（我们叫X，或者特征），和数据的标注（我们叫Y），找到x和y之间的对应关系，或者说是函数f。回归分析是一种因变量为连续值得监督学习。

问题

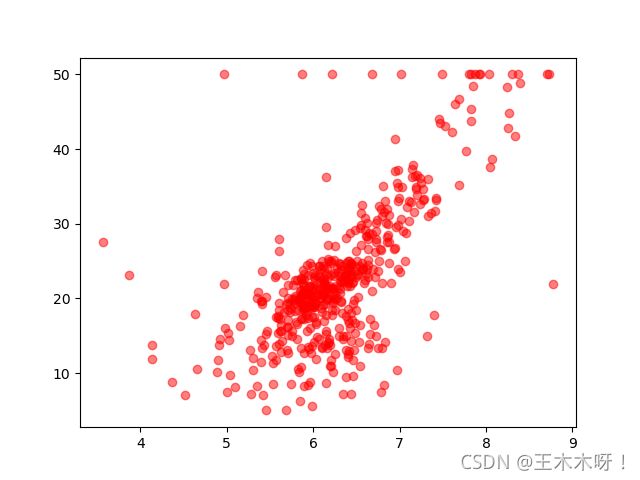
我们有现有问题，统计波士顿房价与所处位置之间的关系，得到数据如下。

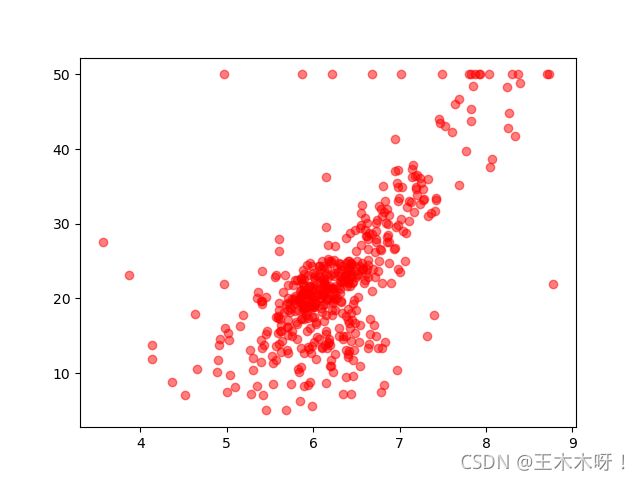
现在需要用一条直线将数据尽可能好的表示出来。

分析问题

第一步

这条直线应该是y_hat=k*x+b
数据已经有了，我们要做的就是将这条直线表示出来。
纸条直线中四个字母，x和y分别是自变量和因变量。所以我们需要猜的其实是k和b两个变量。
所以用如下代码随机出两个值并附给k和b

k = random.randint(0, 50)
b = random.randint(-50, 50)

最后对应求y_hat的函数就应该是：

def y_guess(k, x, b):
    return k * x + b

第二步

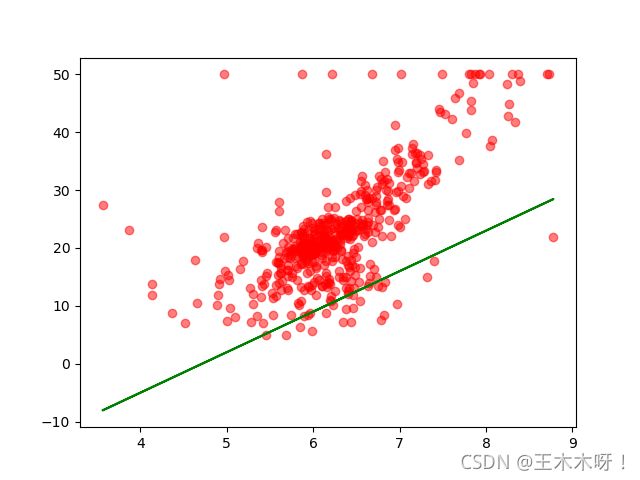
我们随机猜出的直线可以将图片画出来

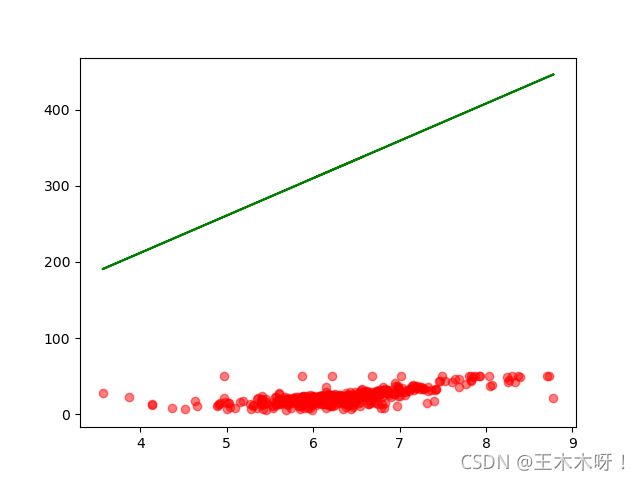
很明显通过人眼，一眼就可以看出效果并不是太好
但是如果用计算机来判断就只能通过书值，所以引入一个叫做损失函数的东西。
$$L{2}_{Loss}=\frac{\sum (Y_{true}-Y_{hat}{)}^2}{n}$$
损失函数越大代表线预测的越差。
根据公式可以知道求损失函数的函数需要传入的值有y_true和y_hat。其中的n可以通过numpy自己求出来，所以不需要传参。
函数实现：

# 求损失
def l2_loss(y_ture, y_guess):
    return np.mean((np.array(y_ture) - np.array(y_guess)) ** 2)

第三步

学习过程：
学习的过程需要对损失函数求偏导。
把k和b当作变量分别对k，b求偏导。
对b求偏导得到的结果: $-2\ast \frac{\sum Y_{true}-Y_{hat}}{n}$

对k求偏导得到的结果: $-2\ast \frac{\sum X\ast (Y_{true}-Y_{hat)}}{n}$
函数实现：
对b求偏导：

def partial_b(y_ture, y_guess):
    return -2 * np.mean((np.array(y_ture) - np.array(y_guess)))

对k求偏导：

def partial_k(y_ture, y_guess, x):
    return -2 * np.mean((np.array(y_ture) - np.array(y_guess)) * np.array(x))

第四步

计算机进行学习

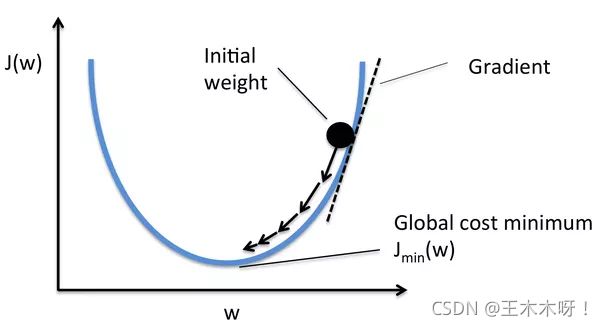
学习的过程就是找到更合适的k还有b的过程，如上图所示，达到最合适的点也就是图像的最低点。所以学习的公式是：
$$k=k-lr\ast \frac{\sigma loss}{\sigma k}$$

$$b=b-lr\ast \frac{\sigma loss}{\sigma b}$$
其中lr代表learning_rate是学习率的意思，因为我们在学习的过程中会不断波动，所以为了达到最好的效果，最好不要把学习率设置过大或过小，过大会使波动太大，不宜达到最佳效果。过小会使学习训练时间过长。所以设置一个合适的学习率也是机器学习中一个重要部分。偏导相当于代表斜率，我要达到最低点，不论怎么样都要做减法而不是加法。
学习过程的代码：

    k = k - partial_k(Y, yhat, X_rm) * learning_rate
    b = b - partial_b(Y, yhat) * learning_rate

算法步骤

1. 随机出k，b两个值。
2. 计算损失L2_loss。
3. 对k，b两个值求偏导。
4. 通过偏导来进行学习。

完整代码

from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import random
import numpy as np
# 出图像

# 得到了X,Y
data = load_boston()
X, Y = data['data'], data['target']
room_index = 5
X_rm = X[:, room_index]
print(X.shape)


# 求偏导
# 对k求

def partial_k(y_ture, y_guess, x):
    return -2 * np.mean((np.array(y_ture) - np.array(y_guess)) * np.array(x))

# 对b求
def partial_b(y_ture, y_guess):
    return -2 * np.mean((np.array(y_ture) - np.array(y_guess)))
# 求损失
def l2_loss(y_ture, y_guess):
    return np.mean((np.array(y_ture) - np.array(y_guess)) ** 2)


# y_hat
def y_guess(k, x, b):
    return k * x + b


trying_time = 20000
min_loss = float('inf')
best_k, best_b = None, None
learning_rate = 1e-4
k = random.randint(0, 50)
b = random.randint(-50, 50)

plt.figure()
plt.scatter(X_rm, Y, color='red', alpha=0.5)
plt.figure()
plt.scatter(X_rm, Y, color='red', alpha=0.5)
plt.plot(X_rm, y_guess(k, X_rm, b), color='green')
plt.show()



for i in range(trying_time):
    # 将当前损失于最小损失相比较
    yhat = y_guess(k, X_rm, b)
    L2_loss = l2_loss(Y, yhat)

    if L2_loss < min_loss:
        best_k = k
        best_b = b
        min_loss = L2_loss

    # 找更合适的k与b

    k = k - partial_k(Y, yhat, X_rm) * learning_rate
    b = b - partial_b(Y, yhat) * learning_rate
print('L2loss=', min_loss)
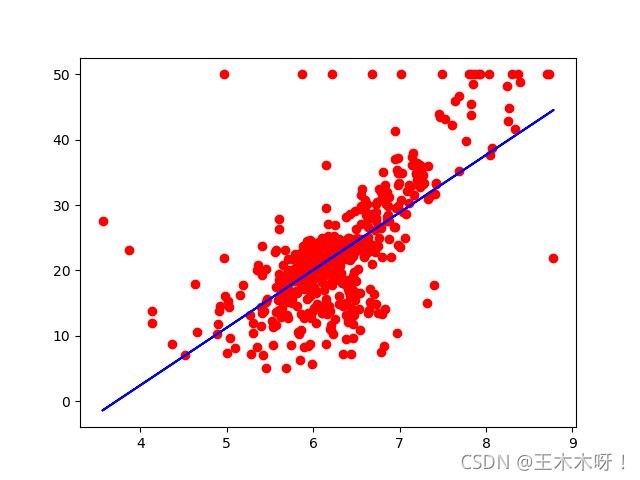
plt.scatter(X_rm, Y, color='red')
plt.plot(X_rm, y_guess(best_k, X_rm, best_b), color='blue')
print('y = {} * x {}'.format(best_k, best_b))
plt.show()

得到图像：