贝叶斯统计：马尔科夫链的生成代码实现
Python实现
马尔科夫链的生成
Trcae_plot图
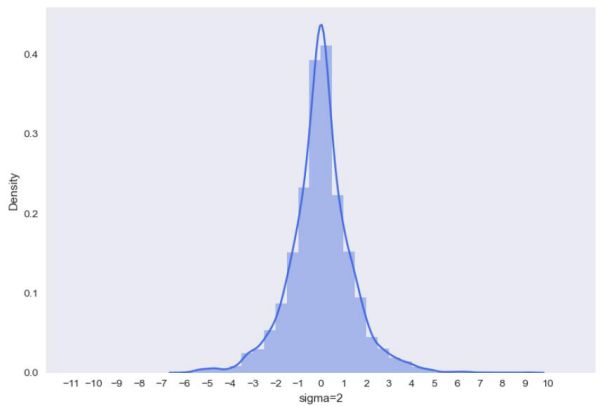
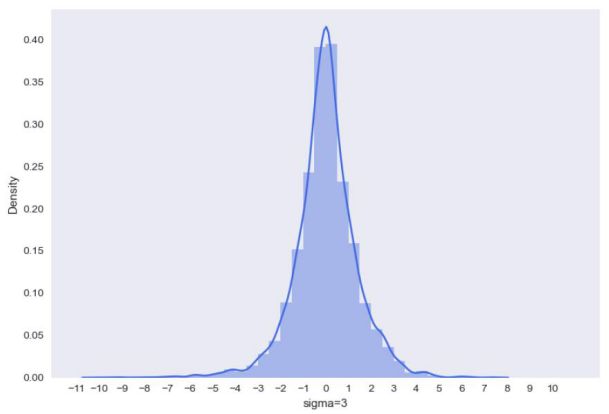
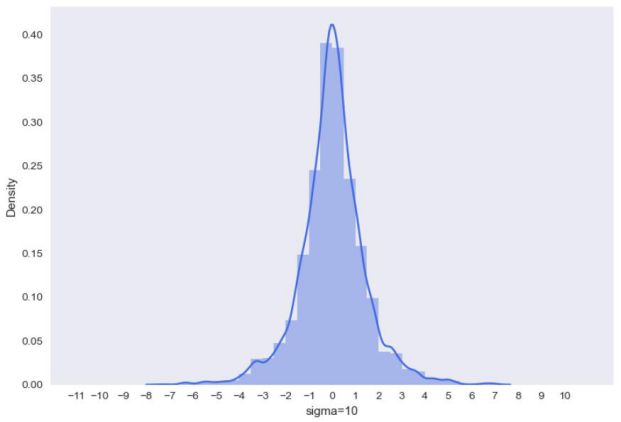
密度直方图
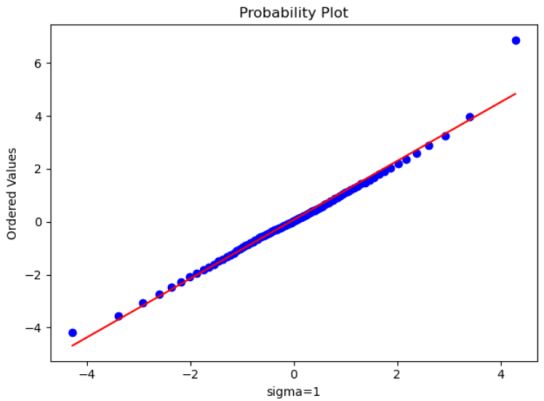
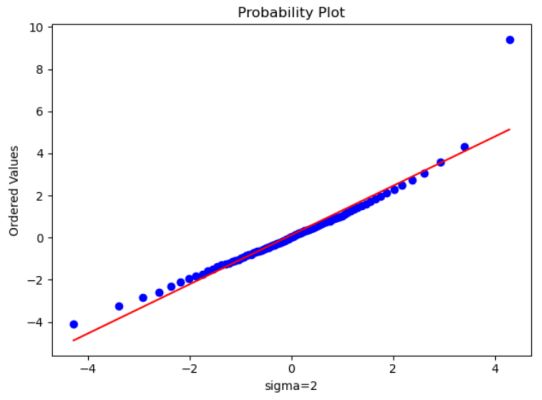
QQ图
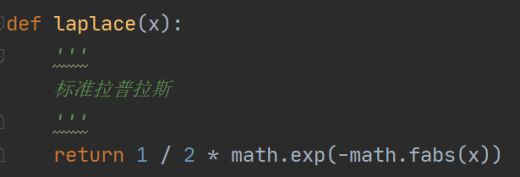
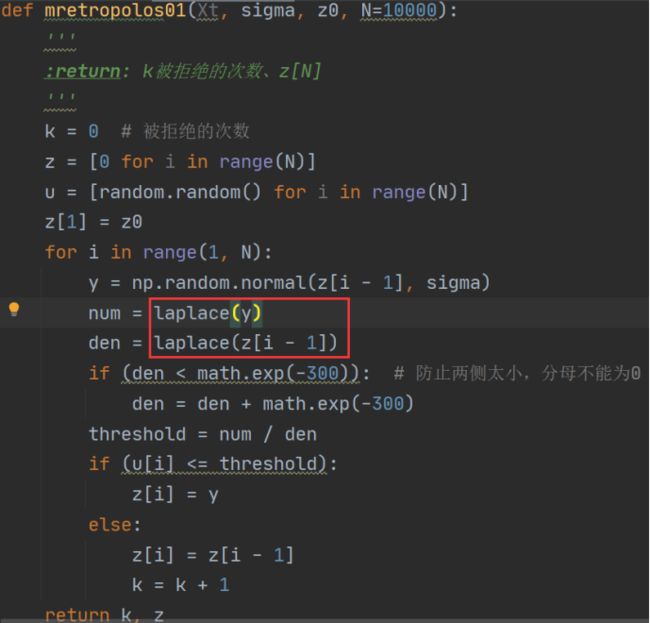
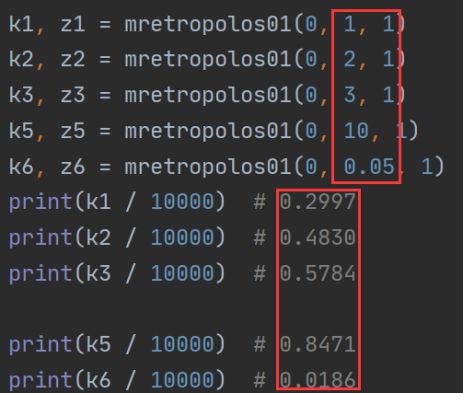
Sigma为1、2是比较合适的 [0.15,0.5]
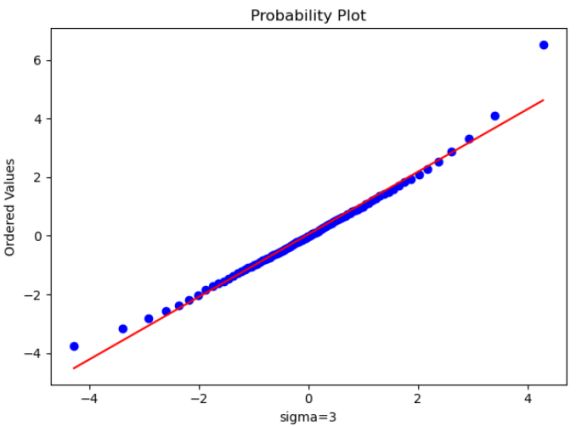
Sigma为3的时候超出0.5一些
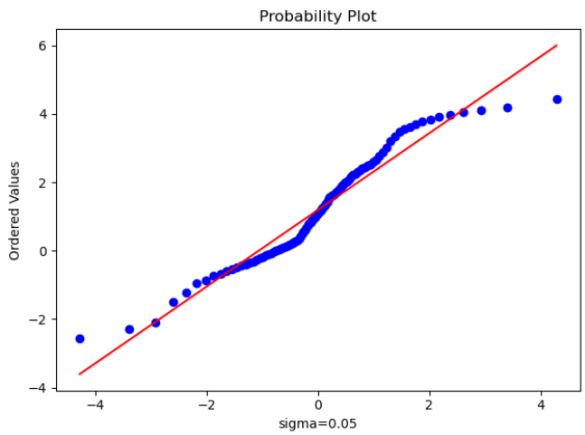
Sigma为0.05的时候很难收敛
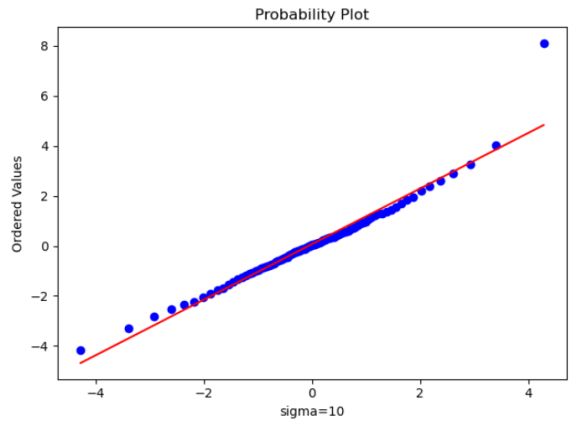
Sigma为10的时候波动很大
Trcae_plot图
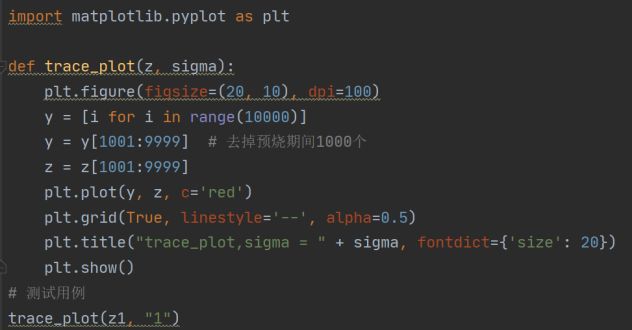
Trace_plot图展示
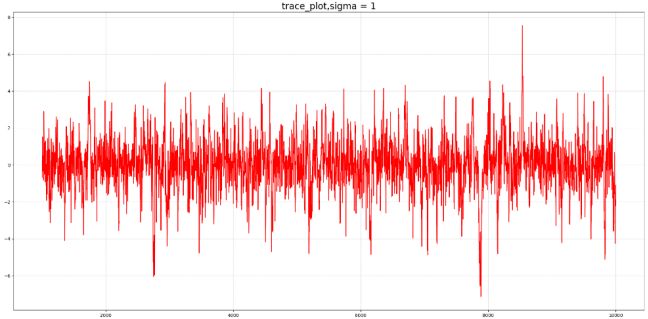
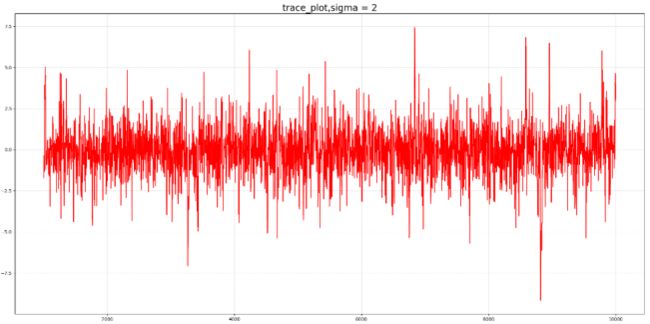
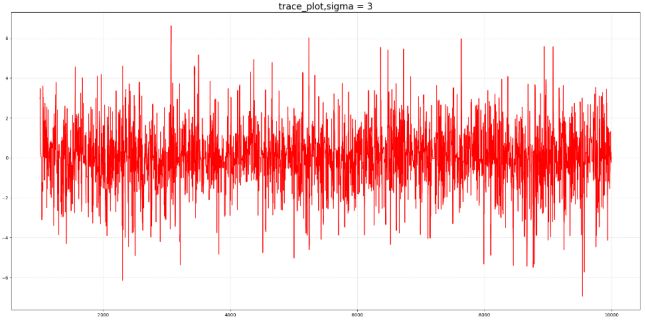
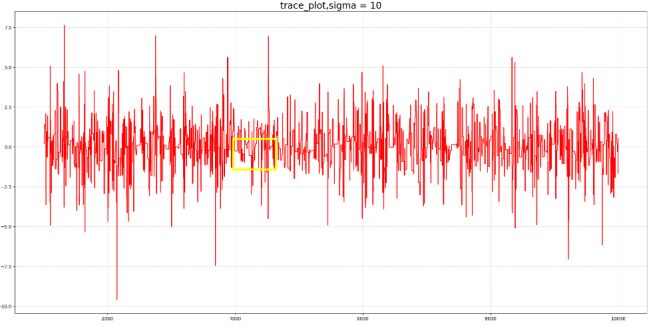
Sigma=10的时候拒绝率高，如果黄框标注的，存在很多平稳的直线。
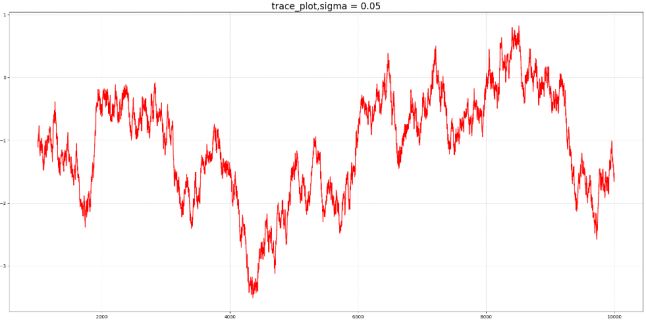
很难收敛
密度直方图
值都集中在0附近。
QQ图
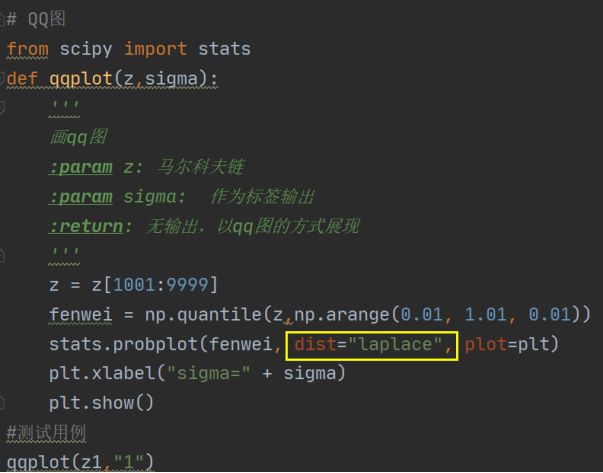
这是最快的实现方法。（有不使用stats包，拿两个函数作对应的图）
简单介绍：
scipy.stats.probplot(x, sparams=(), dist=‘norm’, fit=True, plot=None, rvalue=False)
计算概率图的分位数，并可选地显示该图。生成样本数据相对于指定理论分布(默认为正态分布)的分位数的概率图。
参数：
x：array_like
从哪个样本/响应数据probplot创建情节。
sparams：tuple, 可选参数
Distribution-specific形状参数(形状参数加上位置和比例)。
dist：str 或 stats.distributions instance, 可选参数
分发或分发函数名称。对于正常概率图，默认值为‘norm’。看起来像stats.distributions实例的对象(即它们具有一个ppf方法)也被接受。在本例中直接使用柯西分布，也可以使用自由度为1的t分布。
fit：bool, 可选参数
如果为True(默认值)，则将least-squares回归(best-fit)行拟合到样本数据。
plot：object, 可选参数
如果给定，则绘制分位数和最小二乘拟合。 plot是必须具有方法“plot”和“text”的对象。的matplotlib.pyplot可以使用模块或Matplotlib Axes对象，也可以使用具有相同方法的自定义对象。默认值为“无”，这意味着不创建任何图。
图形展示：
Sigma=0.05的时候拟合不太好，其余拟合状态普遍不错，根据斜率来看，sigma=1相对更合适。