BP神经网络算法
算法介绍
BP神经网络算法是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。
算法详解
BP神经网络图
最简单的BP神经网络有三层,分别是输入层,隐含层,输出层,如图:
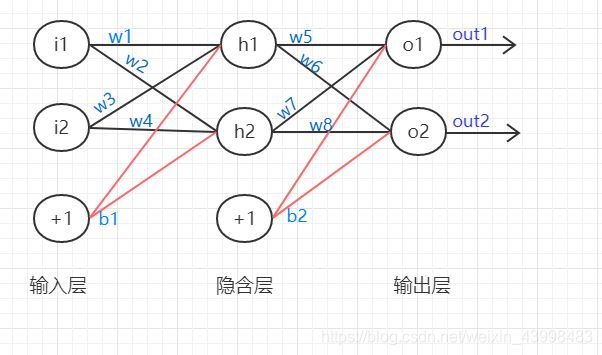
那么BP神经网络算法是怎么进行训练和计算的呢?计算流程如下:
- 对神经网络的权值(wi)和偏置值(b)进行随机赋值
- 求隐含层各点的加权和 :
h1的加权和:
S h 1 = i 1 ∗ w 1 + i 2 ∗ w 3 + b 1 ∗ 1 S_{h_1}=i_1*w_1+i_2*w_3+b_1*1 Sh1=i1∗w1+i2∗w3+b1∗1
h2的加权和:
S h 2 = i 1 ∗ w 2 + i 2 ∗ w 4 + b 1 ∗ 1 S_{h_2}=i_1*w_2+i_2*w_4+b_1*1 Sh2=i1∗w2+i2∗w4+b1∗1 - 求隐含层的输出
h1的输出为:
O h 1 = 1 1 + e − S h 1 O_{h_1}=\frac{1}{1+e^{-S_{h_1}}} Oh1=1+e−Sh11
h2的输出为:
O h 2 = 1 1 + e − S h 2 O_{h_2}=\frac{1}{1+e^{-S_{h_2}}} Oh2=1+e−Sh21 - 相同方法计算o1和o2的输出值:
o1、o2的加权和如下:
S o 1 = O h 1 ∗ w 5 + O h 2 ∗ w 7 + b 2 ∗ 1 S_{o_1}=O_{h_1}*w_5+O_{h_2}*w_7+b_2*1 So1=Oh1∗w5+Oh2∗w7+b2∗1
S o 2 = O h 1 ∗ w 6 + O h 2 ∗ w 8 + b 2 ∗ 1 S_{o_2}=O_{h_1}*w_6+O_{h_2}*w_8+b_2*1 So2=Oh1∗w6+Oh2∗w8+b2∗1
由此可得最终输出值如下:
O o 1 = 1 1 + e − S o 1 O_{o_1}=\frac{1}{1+e^{-S_{o_1}}} Oo1=1+e−So11
O o 2 = 1 1 + e − S o 2 O_{o_2}=\frac{1}{1+e^{-S_{o_2}}} Oo2=1+e−So21 - 反向计算误差
设目标输出 O o 1 = T 1 , O o 1 = T 2 O_{o_1}=T_1,O_{o_1}=T_2 Oo1=T1,Oo1=T2
总误差 E = E o 1 + E o 2 E=E_{o_1}+E_{o_2} E=Eo1+Eo2
E o 1 = O o 1 ( 1 − O o 1 ) ( T 1 − O o 1 ) E_{o_1}=O_{o_1}(1-O_{o_1})(T_1-O_{o_1}) Eo1=Oo1(1−Oo1)(T1−Oo1)
E o 2 = O o 2 ( 1 − O o 2 ) ( T 2 − O o 2 ) E_{o_2}=O_{o_2}(1-O_{o_2})(T_2-O_{o_2}) Eo2=Oo2(1−Oo2)(T2−Oo2) - 进行输出层到隐含层的权值更新
∂ E ∂ w 5 = ∂ E ∂ O o 1 ∗ ∂ O o 1 ∂ S o 1 ∗ ∂ S o 1 ∂ w 5 \frac{\partial E}{\partial w_5}=\frac{\partial E}{\partial O_{o_1}}*\frac{\partial O_{o_1}}{\partial S_{o_1}}*\frac{\partial S_{o_1}}{\partial w_5} ∂w5∂E=∂Oo1∂E∗∂So1∂Oo1∗∂w5∂So1
w 5 + = w 5 − 学 习 效 率 ∗ ∂ E ∂ w 5 {w_5}^+=w_5-学习效率* \frac{\partial E}{\partial w_5} w5+=w5−学习效率∗∂w5∂E - 进行隐含层到输入层的权值更新
隐含层到输出层的权值更新其实是换汤不换药,只是要注意的是隐含层的每个点的误差并不只是来自输出层一个点。如h1的误差值和o1,o2均有关系,所以:
∂ E ∂ w 1 = ∂ E ∂ O h 1 ∗ ∂ O h 1 ∂ S h 1 ∗ ∂ S h 1 ∂ w 1 \frac{\partial E}{\partial w_1}=\frac{\partial E}{\partial O_{h_1}}*\frac{\partial O_{h_1}}{\partial S_{h_1}}*\frac{\partial S_{h_1}}{\partial w_1} ∂w1∂E=∂Oh1∂E∗∂Sh1∂Oh1∗∂w1∂Sh1
而
∂ E ∂ O h 1 = ∂ E o 1 ∂ O h 1 + ∂ E o 2 ∂ O h 1 \frac{\partial E}{\partial O_{h_1}}=\frac{\partial E_{o_1}}{\partial O_{h_1}}+\frac{\partial E_{o_2}}{\partial O_{h_1}} ∂Oh1∂E=∂Oh1∂Eo1+∂Oh1∂Eo2 - 权值更新完后经过重新计算不断迭代直到误差降到最小,让输出图像无限逼近目标图像。
算法实现
BP算法:
% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
% 输入两个元素的向量,第一层有三个神经元(3),第二层有一个神经元(1)。
% 第一层的传递函数是tan-sigmoid,输出层的传递函数是linear。 输入向量的第一个元素的范围是-1到2[-1 2],输入向量的第二个元素的范围是0到5[0 5], 训练函数是traingd。 [-1 2]
net.IW{1}%输入层到隐含层的权重矩阵,全部为1?
net.b{1}%阈值向量,全部为1?
p=[1;2];
% p=[1
% 2]
a=sim(net,p)%执行simulink模型
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
%net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)%符号函数
a3=tansig(a2)%双曲正切S型传输函数
a4=purelin(a3)%线性传输函数
net.b{2}%阈值均设为2
net.b{1}%阈值均设为1
net.IW{1}%权重矩阵均为1
net.IW{2}%权重矩阵均为2
0.7616+net.b{2}%阈值加上0.7616
a-net.b{2}
(a-net.b{2})/0.7616;
help purelin
p1=[0;0];
a5=sim(net,p1)
net.b{2}
% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}
%p=[1;];
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}
P=[1.2;3;0.5;1.6]
W=[0.3 0.6 0.1 0.8]
net1=newp([0 2;0 2;0 2;0 2],1,'purelin');
net2=newp([0 2;0 2;0 2;0 2],1,'logsig');
net3=newp([0 2;0 2;0 2;0 2],1,'tansig');
net4=newp([0 2;0 2;0 2;0 2],1,'hardlim');
net1.IW{1}
net2.IW{1}
net3.IW{1}
net4.IW{1}
net1.b{1}
net2.b{1}
net3.b{1}
net4.b{1}
net1.IW{1}=W;
net2.IW{1}=W;
net3.IW{1}=W;
net4.IW{1}=W;
a1=sim(net1,P)
a2=sim(net2,P)
a3=sim(net3,P)
a4=sim(net4,P)
init(net1);
net1.b{1}
help tansig
% 训练
p=[-0.1 0.5]
t=[-0.3 0.4]
w_range=-2:0.4:2;
b_range=-2:0.4:2;
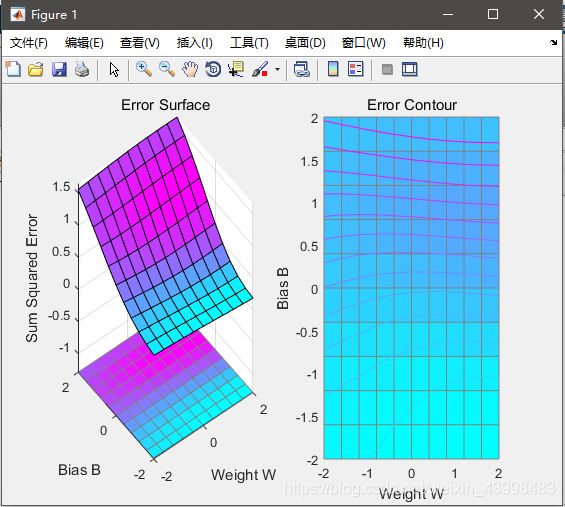
ES=errsurf(p,t,w_range,b_range,'logsig');%单输入神经元的误差曲面
plotes(w_range,b_range,ES)%绘制单输入神经元的误差曲面
pause(0.5);
hold off;
net=newp([-2,2],1,'logsig');
net.trainparam.epochs=100;
net.trainparam.goal=0.001;
figure(2);
[net,tr]=train(net,p,t);
title('动态逼近')
wight=net.iw{1}
bias=net.b
pause;
close;
% 练
p=[-0.2 0.2 0.3 0.4]
t=[-0.9 -0.2 1.2 2.0]
h1=figure(1);
net=newff([-2,2],[5,1],{'tansig','purelin'},'trainlm');
net.trainparam.epochs=100;
net.trainparam.goal=0.0001;
net=train(net,p,t);
a1=sim(net,p)
pause;
h2=figure(2);
plot(p,t,'*');
title('样本')
title('样本');
xlabel('Input');
ylabel('Output');
pause;
hold on;
ptest1=[0.2 0.1]
ptest2=[0.2 0.1 0.9]
a1=sim(net,ptest1);
a2=sim(net,ptest2);
net.iw{1}
net.iw{2}
net.b{1}
net.b{2}% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}%偏置值
p=[1;2];
% p=[1
% 2]
a=sim(net,p)%执行simulink模型
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
%net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)%符号函数
a3=tansig(a2)%双曲正切S型传输函数
a4=purelin(a3)%线性传输函数
net.b{2}
net.b{1}
net.IW{1}
net.IW{2}
0.7616+net.b{2}
a-net.b{2}
(a-net.b{2})/0.7616;
help purelin
p1=[0;0];
a5=sim(net,p1)
net.b{2}
% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}
%p=[1;];
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}
P=[1.2;3;0.5;1.6]
W=[0.3 0.6 0.1 0.8]
net1=newp([0 2;0 2;0 2;0 2],1,'purelin');%newp:创建感知神经网络
net2=newp([0 2;0 2;0 2;0 2],1,'logsig');
net3=newp([0 2;0 2;0 2;0 2],1,'tansig');
net4=newp([0 2;0 2;0 2;0 2],1,'hardlim');
net1.IW{1}
net2.IW{1}
net3.IW{1}
net4.IW{1}
net1.b{1}
net2.b{1}
net3.b{1}
net4.b{1}
net1.IW{1}=W;
net2.IW{1}=W;
net3.IW{1}=W;
net4.IW{1}=W;
a1=sim(net1,P)
a2=sim(net2,P)
a3=sim(net3,P)
a4=sim(net4,P)
init(net1);
net1.b{1}
help tansig
% 训练
p=[-0.1 0.5]
t=[-0.3 0.4]
w_range=-2:0.4:2;
b_range=-2:0.4:2;
ES=errsurf(p,t,w_range,b_range,'logsig');%单输入神经元的误差曲面
plotes(w_range,b_range,ES)%绘制单输入神经元的误差曲面
pause(0.5);
hold off;
net=newp([-2,2],1,'logsig');
net.trainparam.epochs=100;
net.trainparam.goal=0.001;
figure(2);
[net,tr]=train(net,p,t);
title('动态逼近')
wight=net.iw{1}
bias=net.b
pause;
close;
% 练
p=[-0.2 0.2 0.3 0.4]
t=[-0.9 -0.2 1.2 2.0]
h1=figure(1);
net=newff([-2,2],[5,1],{'tansig','purelin'},'trainlm');
net.trainparam.epochs=100;
net.trainparam.goal=0.0001;
net=train(net,p,t);
a1=sim(net,p)
pause;
h2=figure(2);
plot(p,t,'*');
title('样本')
title('样本');
xlabel('Input');
ylabel('Output');
pause;
hold on;
ptest1=[0.2 0.1]
ptest2=[0.2 0.1 0.9]
a1=sim(net,ptest1);
a2=sim(net,ptest2);
net.iw{1}
net.iw{2}
net.b{1}
net.b{2}
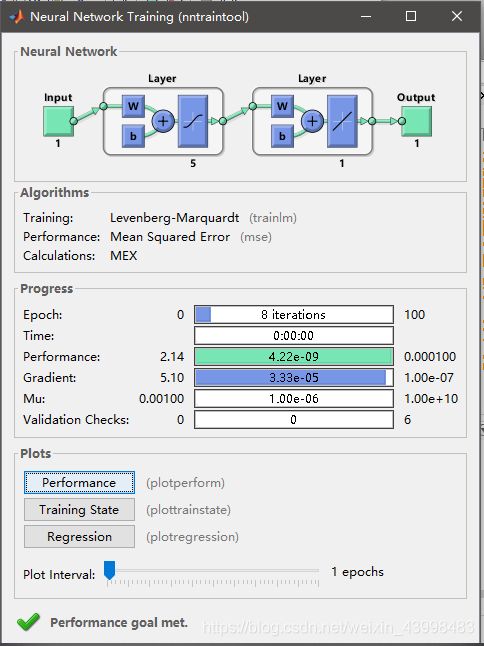
运行结果
% B 第一章 感知器
% 1. 感知器神经网络的构建
% 1.1 生成网络
net=newp([0 2],1);%单输入,输入值为[0,2]之间的数
inputweights=net.inputweights{1,1};%第一层的权重为1
biases=net.biases{1};%阈值为1
% 1.2 网络仿真
net=newp([-2 2;-2 2],1);%两个输入,一个神经元,默认二值激活
net.IW{1,1}=[-1 1];%权重,net.IW{i,j}表示第i层网络第j个神经元的权重向量
net.IW{1,1}
net.b{1}=1;
net.b{1}
p1=[1;1],a1=sim(net,p1)
p2=[1;-1],a2=sim(net,p2)
p3={[1;1] [1 ;-1]},a3=sim(net,p3) %两组数据放一起
p4=[1 1;1 -1],a4=sim(net,p4)%也可以放在矩阵里面
net.IW{1,1}=[3,4];
net.b{1}=[1];
a1=sim(net,p1)
% 1.3 网络初始化
net=init(net);
wts=net.IW{1,1}
bias=net.b{1}
% 改变权值和阈值为随机数
net.inputweights{1,1}.initFcn='rands';
net.biases{1}.initFcn='rands';
net=init(net);
bias=net.b{1}
wts=net.IW{1,1}
a1=sim(net,p1)
% 2. 感知器神经网络的学习和训练
% 1 网络学习
net=newp([-2 2;-2 2],1);
net.b{1}=[0];
w=[1 -0.8]
net.IW{1,1}=w;
p=[1;2];
t=[1];
a=sim(net,p)
e=t-a
help learnp
dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
w=w+dw
net.IW{1,1}=w;
a=sim(net,p)
net = newp([0 1; -2 2],1);
P = [0 0 1 1; 0 1 0 1];
T = [0 1 1 1];
Y = sim(net,P)
net.trainParam.epochs = 20;
net = train(net,P,T);
Y = sim(net,P)
% 2 网络训练
net=init(net);
p1=[2;2];t1=0;p2=[1;-2];t2=1;p3=[-2;2];t3=0;p4=[-1;1];t4=1;
net.trainParam.epochs=1;
net=train(net,p1,t1)
w=net.IW{1,1}
b=net.b{1}
a=sim(net,p1)
net=init(net);
p=[[2;2] [1;-2] [-2;2] [-1;1]];
t=[0 1 0 1];
net.trainParam.epochs=1;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=2;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=20;
net=train(net,p,t);
a=sim(net,p)
% 3. 二输入感知器分类可视化问题
P=[-0.5 1 0.5 -0.1;-0.5 1 -0.5 1];
T=[1 1 0 1]
net=newp([-1 1;-1 1],1);
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1});
%hold on;
%plotpv(P,T);
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1})
net.adaptParam.passes=3;
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpc(net.IW{1},net.b{1})
net.adaptParam.passes=6;
net=adapt(net,P,T)
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1},net.b{1})
plotpc(net.IW{1},net.b{1})
%仿真
a=sim(net,p);
plotpv(p,a)
p=[0.7;1.2]
a=sim(net,p);
plotpv(p,a);
hold on;
plotpv(P,T);
plotpc(net.IW{1},net.b{1})
%感知器能够正确分类,从而网络可行。
% 4. 标准化学习规则训练奇异样本
P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50]
T=[1 1 0 0 1];
net=newp([-40 1;-1 50],1);
plotpv(P,T);%标出所有点
hold on;
linehandle=plotpc(net.IW{1},net.b{1});%画出分类线
E=1;
net.adaptParam.passes=3;%passes决定在训练过程中训练值重复的次数。
while (sse(E))
[net,Y,E]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%另外一种网络修正学习(非标准化学习规则learnp)
hold off;
net=init(net);
net.adaptParam.passes=3;
net=adapt(net,P,T);
plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%无法正确分类
%标准化学习规则网络训练速度要快!
% 训练奇异样本
% 用标准化感知器学习规则(标准化学习数learnpn)进行分类
net=newp([-40 1;-1 50],1,'hardlim','learnpn');
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net.adaptParam.passes=3;
net=init(net);
linehandle=plotpc(net.IW{1},net.b{1});
while (sse(e))
[net,Y,e]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
end;
axis([-2 2 -2 2]);
net.IW{1}%权重
net.b{1}%阈值
%正确分类
%非标准化感知器学习规则训练奇异样本的结果
net=newp([-40 1;-1 50],1);
net.trainParam.epochs=30;
net=train(net,P,T);
pause;
linehandle=plotpc(net.IW{1},net.b{1});
hold on;
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
% 5. 设计多个感知器神经元解决分类问题
p=[1.0 1.2 2.0 -0.8; 2.0 0.9 -0.5 0.7]
t=[1 1 0 1;0 1 1 0]
plotpv(p,t);
hold on;
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net=init(net);
while (sse(e))
[net,y,e]=adapt(net,p,t);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;
实现效果:
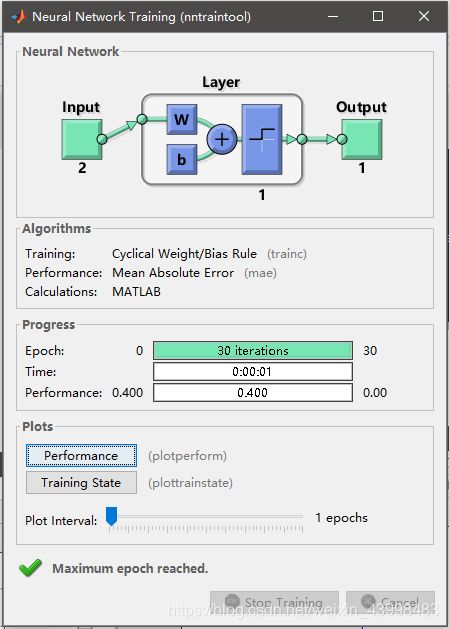
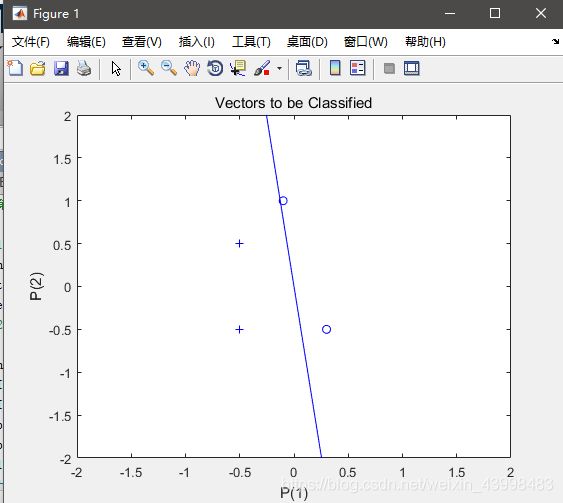
输入0之后:
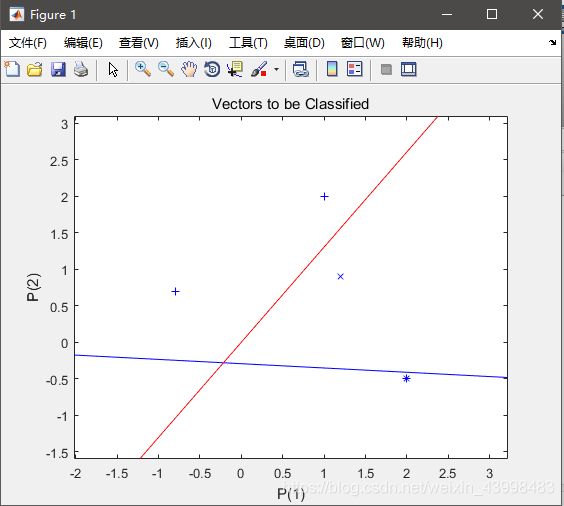
BP算法优缺点:
优点:能够自主学习,达到最接近目标值的输出
缺点:参数过多,调整参数大小会占用非常多的时间
有可能会训练失败