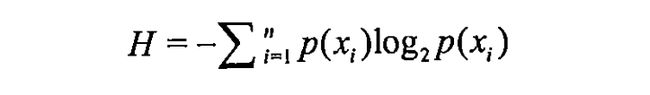机器学习——决策树
定义:
决策树(Decision Tree,又称为判定树)算法是机器学习中常见的一类算法,是一种以树结构(包括二叉树和多叉树)形式表达的预测分析模型。每个决策点实现一个具有离散输出的测试函数,记为分支。决策树由结点和有向边组成。结点有两种类型: 内部结点和叶节点。内部节点表示一个特征或属性,叶节点表示一个类。
决策树的一般流程:
(1)收集数据:可以使用任何方法。
(2)准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
(3)分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
(4)训练算法:构造树的数据结构。
(5)测试算法:使用经验树计算错误率。
(6)使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据
的内在含义。
例子:
相亲确实是一个决策的过程,比如女方对男方身高、学历、工作、家庭等特征与自己心里预期进行比较,比较的过程就是一个决策的过程,决策的结果就是女方愿不愿意与男方谈对象。
![]()
信息增益
划分数据集的大原则是:将无序的数据变的更加有序。我们可以使用多种方法划分数据集,但是每种方法都有各自的优缺点。在众多划分方法中评测出最好的划分方式之前,我们必须学习如何计算信息增益。集合信息的度量方式称为香农熵或者简称为熵。
熵定义为信息的期望值,在明晰这个概念之前,我们必须知道信息的定义。如果待分类的事务可能划分在多个分类之中,则符号xi的信息定义为
其中p(xi)是选择该分类的概率。
为了计算熵,我们需要计算所有类别所有可能包含的信息期望值,通过下面的公式得到:
其中n是分类的数目。
实例:
weather天气(1晴朗,0下雨) trans交通(1顺畅,0拥堵) result是否出去玩(yes,no)
数据集:
计算信息熵代码:
可以根据信息熵,按照获取最大信息增益的方法划分数据集
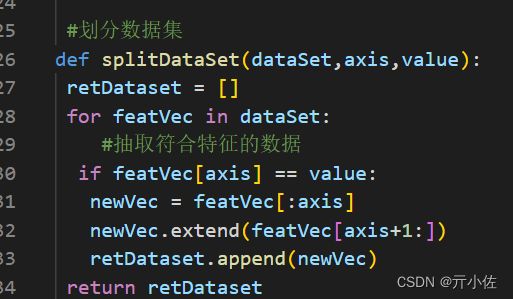
划分数据集:
划分数据集就是将所有符合要求的元素抽出来
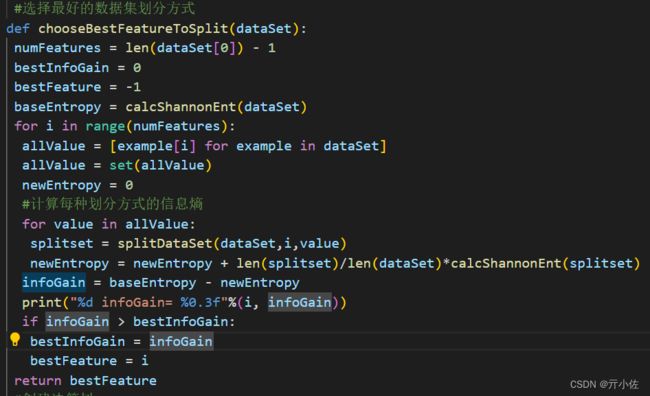
选择最好的数据集划分方式
信息增益是熵的减少或者是信息无序度的减少
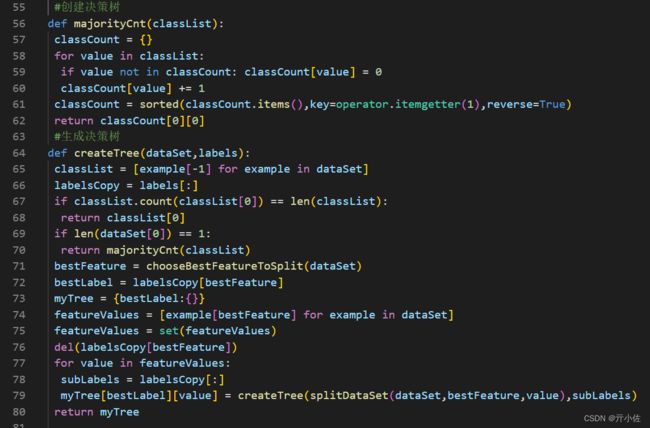
递归创建决策树:
结束条件为:程序遍历完所有划分数据集的属性,或每个分支下的所有实例都具有相同的分类。
当数据集已经处理了所有属性,但是类标签还不唯一时,采用多数表决的方式决定叶子节点的类型。
使用决策树进行分类:
同样采用递归的方式得到分类结果
实验结果:
完整代码:
import numpy as np
import math
import operator
def createDataSet():
dataSet = [[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],]
label = ['no surfacing','flippers']
return dataSet,label
#计算信息熵
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
#为所有可能分类创建字典
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts:
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0
for key in labelCounts:
shannonEnt = shannonEnt - (labelCounts[key]/numEntries)*math.log2(labelCounts[key]/numEntries)
return shannonEnt
#划分数据集
def splitDataSet(dataSet,axis,value):
retDataset = []
for featVec in dataSet:
#抽取符合特征的数据
if featVec[axis] == value:
newVec = featVec[:axis]
newVec.extend(featVec[axis+1:])
retDataset.append(newVec)
return retDataset
#选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
bestInfoGain = 0
bestFeature = -1
baseEntropy = calcShannonEnt(dataSet)
for i in range(numFeatures):
allValue = [example[i] for example in dataSet]
allValue = set(allValue)
newEntropy = 0
#计算每种划分方式的信息熵
for value in allValue:
splitset = splitDataSet(dataSet,i,value)
newEntropy = newEntropy + len(splitset)/len(dataSet)*calcShannonEnt(splitset)
infoGain = baseEntropy - newEntropy
print("%d infoGain= %0.3f"%(i, infoGain))
if infoGain > bestInfoGain:
bestInfoGain = infoGain
bestFeature = i
return bestFeature
#创建决策树
def majorityCnt(classList):
classCount = {}
for value in classList:
if value not in classCount: classCount[value] = 0
classCount[value] += 1
classCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return classCount[0][0]
#生成决策树
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
labelsCopy = labels[:]
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeature = chooseBestFeatureToSplit(dataSet)
bestLabel = labelsCopy[bestFeature]
myTree = {bestLabel:{}}
featureValues = [example[bestFeature] for example in dataSet]
featureValues = set(featureValues)
del(labelsCopy[bestFeature])
for value in featureValues:
subLabels = labelsCopy[:]
myTree[bestLabel][value] = createTree(splitDataSet(dataSet,bestFeature,value),subLabels)
return myTree
#使用决策树分类
def classify(inputTree,featLabels,testVec):
currentFeat = list(inputTree.keys())[0]
secondTree = inputTree[currentFeat]
try:
featureIndex = featLabels.index(currentFeat)
except ValueError as err:
print('yes')
try:
for value in secondTree.keys():
if value == testVec[featureIndex]:
if type(secondTree[value]).__name__ == 'dict':
classLabel = classify(secondTree[value],featLabels,testVec)
else:
classLabel = secondTree[value]
return classLabel
except AttributeError:
print(secondTree)
if __name__ == "__main__":
dataset,label = createDataSet()
myTree = createTree(dataset,label)
a = [1,1]
print(classify(myTree,label,a))