OpenCV入门系列4：图像梯度常用算子——Sobel,Scharr和Laplacian算子

前言

系列3已经初步进入梯度的计算，接下来将对应用于图像梯度的算子引入和展示，包括Sobel算子、Schaar算子和Laplacian算子。

一、Sobel算子

不同与系列3中，膨胀操作减去腐蚀操作得到的梯度，使用Sobel算子进行图像梯度的求取更类似于使用一个像素点周围的均值代替该像素点数据。

1.1 算子内容

Sobel算子包含水平与垂直两个方向的矩阵，其分别从水平和垂直方向，对图像数据进行矩阵的点乘运算。

其中，水平方向矩阵如下：
$$\left(\begin{array}{ccc}\text{-}1& 0& +1\\ \text{-}2& 0& +2\\ \text{-}1& 0& +1\end{array}\right)$$
垂直方向矩阵如下：
$$\left(\begin{array}{ccc}\text{-}1& \text{-}2& \text{-}1\\ 0& 0& 0\\ \text{+}1& \text{+}2& +1\end{array}\right)$$
易知，所得到的点乘结果求取均值即可代表矩阵中心点的梯度，作为图像对应位置像素点梯度数据。

注：点乘即为矩阵对应位置元素相乘，所得到数据为点乘之后数据和。
对应到Sobel算子可推断，点乘后水平矩阵结果为：（X13-X11）+2（X23-X-21)+(X33-X31)，即第三列与第一列的权重差值，在除3之后即可得到平均值，作为中心像素点的图像梯度。垂直计算同理。
此外，矩阵中的值是按照距中心点距离所定，越接近中心点所求梯度结果所占权重就越大。

1.2 代码实现

调用Sobel算子计算图像梯度的代码如下所示：

sobelx=cv2.Sobel(pie,cv2.CV_64F,1,0,ksize=3)
sobely=cv2.Sobel(pie,cv2.CV_64F,0,1,ksize=3)
sobelx=cv2.convertScaleAbs(sobelx)
sobely=cv2.convertScaleAbs(sobely)
sobelxy=cv2.addWeighted(sobelx,0.5,sobely,0.5,0)

cv2.Sobel(src,deph,dx,dy,ksize) 函数具有5个参数，分别为：数据，深度，方向，尺寸，其中

• depth:表示图像的深度,通常处理的图像是 8 位图类型，如果结果也是该类型，那么所有负数会自动截断为 0，发生信息丢失。所以，为了避免信息丢失，我们在计算时通常使用更高的数据类型 cv2.CV_64F，后续通过取绝对值将其映射为 cv2.CV_8U（8 位图）类型。
• dx,dy:表示水平和竖直方向，赋值为1,0 则取水平算子，进行水平方向计算；赋值为0,1则取垂直算子，进行垂直方向计算。
• ksize:Sobel算子的大小，一般取3。

cv2.convertScaleAbs() 函数为取绝对值函数，可通过将负值映射为正，从而将图像数据转化为8位图。

cv2.addWeighted() 函数，在图像叠加时介绍过，可将两张图像的数据按照设定权重叠加到一起，此处可将sobelx与sobely叠加至一起，得到完整的图像梯度图。

1.3 结果展示

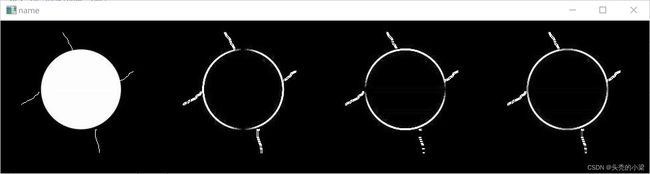
图像分别为初始图像、sobelx 图像、sobely 图像和sobelxy 图像。可以直观看出，sobelx 的上下边缘和sobely的左右边缘均有空白部分，这与算子和图像的对称性有关，但是在叠加后即可弥补该损失。

此外，可通过设置cv2.sobel() 函数dx,dy位置为1,1，直接求两矩阵叠加结果，但是由于直接叠加结果可能会超过范围，从而被截断，导致效果不如使用第一种方法的结果。故一般均采用第一种*cv2.addWeighted()*的方法

二、Scharr算子

Schaar算子与Sobel算子内容基本相同，但是强化了距离对权重的影响，整体运算方法无任何变化。

2.1 算子内容

水平方向矩阵为：

$$\left(\begin{array}{ccc}\text{-3}& 0& +3\\ \text{-}10& 0& +10\\ \text{-}3& 0& +3\end{array}\right)$$
垂直方向矩阵为：

$$\left(\begin{array}{ccc}\text{-3}& -10& +3\\ 0& 0& 0\\ +3& +10& +3\end{array}\right)$$
易知，此算子强化为距离对权重的影响，对较近距离像素点的变化更为敏感，其绘制的图像更为细节，如灰色与黑色区别更加明显等，其余在运算时无任何变化。

2.2 代码实现

scharrx=cv2.Scharr(lena,cv2.CV_64F,1,0)
scharry=cv2.Scharr(lena,cv2.CV_64F,0,1)
scharrx=cv2.convertScaleAbs(scarrx)
scharry=cv2.convertScaleAbs(scarry)
scharrxy=cv2.addWeighted(scarrx,0.5,scarry,0.5,0)

仅将函数中的 sobel 替换为 scharr 即可使用Scharr算子实现图像梯度的计算。

三、Laplacian算子

即拉普拉斯算子，对应拉普拉斯分布，即随着距离的变化，算子矩阵中的内容按照拉普拉斯分布规律变化。其实际意义为图像灰度的二阶导数，即灰度变化率。

拉普拉斯分布即为正态分布, 即u 和 sigma对应的函数

3.1 算子内容

仅具有一个矩阵：
$$\left(\begin{array}{ccc}0& 1& 0\\ 1& 4& 1\\ 0& 1& 0\end{array}\right)$$
本身中心为最高峰，向两边依次减小。当周围和高于中心时，减弱中心像素；当周围和低于中心时，增强中心像素，一般用于图像的锐化。

3.2 实现代码

Laplacian算子仅具有一个矩阵，对应函数参数量有所减少，实现代码如下所示

laplacian=cv2.Laplacian(lena,cv2.CV_64F)
laplacian=cv2.convertScaleAbs(laplacian)

四、三种算子结果对比

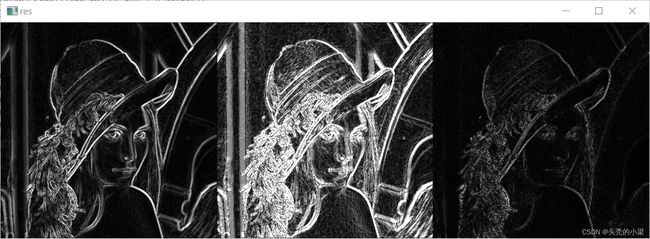
分别对应Sobel算子、Scharr算子和Laplacian算子。易知，前两种算子对比，Scharr算子对比度更强，细节描绘更加详细，而Laplacian算子使灰度的变化率所得到的图像梯度，一般用于图像的锐化。

总结

本节引入了Sobel算子、Scharr算子和Laplacian算子求解图像的梯度，并对结果进行了展示，但对Laplacian算子介绍较为含糊，而且算子不止有三种，所以此处给出参考网站供大家深入学习。

https://blog.csdn.net/weixin_42415138/article/details/108574657