论文阅读笔记——用于图像修复的多尺度特征注意力金字塔：Pyramid Attention Networks for Image Restoration

用于图像修复的多尺度特征注意力金字塔：Pyramid Attention Networks for Image Restoration

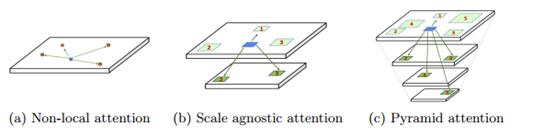
  本文中作者提出了一种新的非局部金字塔注意力的通用模块用于捕获远程依赖关系，提出的注意力基于传统的non-local操作，原始搜索空间从单个特征映射扩展到多尺度特征金字塔。作者的应用方向是图像恢复算法。针对应用在 图像恢复算法当中，其 优势是：

1. 它涵盖了现有的 non-local 操作，在金字塔的最底层特征进行了 non-local 操作。
2. 在金字塔内部的不同尺度的特征的长期依赖关系被明确建模能够得到有效利用。
3. 对于图像恢复：与传统方法类似，人们可能期望通过双三次插值等操作重新缩放到更粗的金字塔级别，可以大大减少特征中的噪声信号。这允许网络从多尺度对应中找到更少噪声的信号。

1.传统non-local模块的问题

传统的non-local计算公式按照非局部均值的定义为：

$$y^i=\frac{1}{\sigma (x)}\sum _j\varphi (x^i,x^j)\theta (x^j)$$

  其中x为输入特征图，i和j为输入x和输出y的索引，函数ϕ用来计算不同位置i和j的相关性信息，$\theta$是特征转换函数，计算j位置的特征值。最后通过函数σ(x)进行归一化。作者分析得到传统Non-local的不足之处，是在单一尺度上进行操作丢失了部分多尺度的信息。

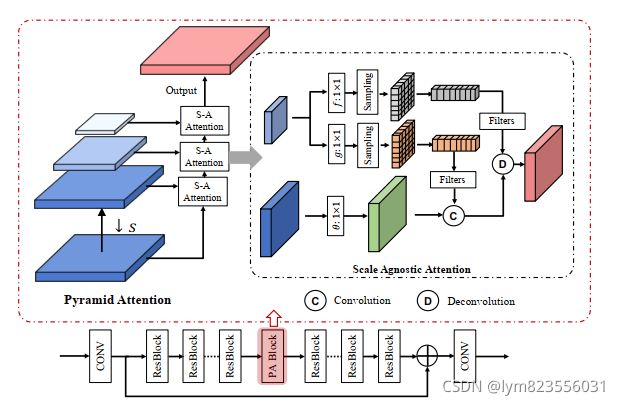
作者为解决这一问题提出了多尺度的non-local模块，如图所示:

图1.(a) 经典的 self-attention 计算相同规模的成对特征相关性。 (b) 尺度不可知注意增强 (a) 以在一个额外的尺度上捕捉对应关系。（c）金字塔注意力通过建模多尺度非局部依赖来​​概括 (a) 和 (b)

输出的最终特征是多尺度特征的加权和。给出不同 scale 的特征S={$1$，$s_1$，$s_2$，….，$s_n$}。公式为：
$$y^i=\frac{1}{\sigma (x)}\sum _{s\in S}\sum _j\varphi (x^i,x_{\delta (s)}^j)\theta (x_{\delta (s)}^j)$$

2.尺度不可知的注意力 Scale Agnostic Attention

上述公式中$\delta$(s)表示输入$x$上的索引$j$为中心的$x^2$邻域。但这样做存在的两个核心问题是：

1. 如何评估$x_{\delta (s)}^2$和$x^j$之间的相关性信息。
2. 如何从$x_{\delta (s)}^2$当中聚合信息成为$y^i$。

  主要的困难出自于不同尺度特征的空间维度的不匹配。之前常见的相似性度量，例如non-local模块常用的 Embedded Gaussian 函数以及 Dot product 函数都只能接受相同维度的特征。为解决这一问题作者将原始输入进行下采样。以两层特征为例得到的公式为：
$$y^i=\frac{1}{\sigma (x,z)}\sum _j\varphi (x^i,z^i)\theta (z^j)$$
  其中z为x在s维度特征的下采样。这种操作带来了额外的优势。将区域缩小为更粗略的描述符会降低噪声水平。另一方面，由于跨尺度递归代表了相似的内容，结构信息在降尺度后仍会得到很好的保存。

3.金字塔注意力 Scale Agnostic Attention

  得到了上述的结论后作者将上述的规模不可知的注意力扩展到了整个金字塔注意力来计算多个尺度之间的相关性。具体来说给定一系列尺度,S={$1$,$s_1$,$s_2$,….,$s_n$}组成了一个特征金字塔F={$F_1,F_2,...,F_n$}，其中$F_i(\frac{H}{s_i}\times \frac{W}{s_i})$是输入$x$通过下采样得到的区域描述符映射。在这种情况下，金字塔的每一层与原始输入$x$的关系均可视为上述尺度不可知的注意力。最终金字塔注意力的表达式为：
$$y^i=\frac{1}{\sigma (x)}\sum _{z\in F}\sum _{j\in Z}\varphi (x_{\delta (r)}^i,z_{\delta (r)}^j)\theta (z^j)$$
  公式当中相似性变换函数$\delta$和特征变换的函数$\theta$分别选择为 embeded gaussian 以及简单的线性变换。
  同时为了提高匹配过程中的鲁棒性，作者还添加了额外的邻域相似度，这与经典的非局部过滤是一致的。其中邻域由 $\delta (r)$ 指定。 这对匹配内容增加了更强的约束，即当且仅当它们的邻域也高度相似时，两个特征高度相关。 逐块匹配允许网络更多地关注相关区域，同时抑制不相关的区域。

整个注意力金字塔模块结构如图所示。

图2. PANet 与文章提出的注意力金字塔(PA)。 Pyramid attention通过连续计算Scale Agnostic (S-A) attention来捕获多尺度的相关性

4.金字塔代码实现

import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import transforms
from torchvision import utils as vutils
from model import common
from utils.tools import extract_image_patches,\
    reduce_mean, reduce_sum, same_padding

class PyramidAttention(nn.Module):
    def __init__(self, level=5, res_scale=1, channel=64, reduction=2, ksize=3, stride=1, softmax_scale=10, average=True, conv=common.default_conv):
        super(PyramidAttention, self).__init__()
        self.ksize = ksize
        self.stride = stride
        self.res_scale = res_scale
        self.softmax_scale = softmax_scale
        self.scale = [1-i/10 for i in range(level)]
        self.average = average
        escape_NaN = torch.FloatTensor([1e-4])
        self.register_buffer('escape_NaN', escape_NaN)
        self.conv_match_L_base = common.BasicBlock(conv,channel,channel//reduction, 1, bn=False, act=nn.PReLU())
        self.conv_match = common.BasicBlock(conv,channel, channel//reduction, 1, bn=False, act=nn.PReLU())
        self.conv_assembly = common.BasicBlock(conv,channel, channel,1,bn=False, act=nn.PReLU())

    def forward(self, input):
        res = input
        #theta
        match_base = self.conv_match_L_base(input)
        shape_base = list(res.size())
        input_groups = torch.split(match_base,1,dim=0)
        # patch size for matching 
        kernel = self.ksize
        # raw_w is for reconstruction
        raw_w = []
        # w is for matching
        w = []
        #build feature pyramid
        for i in range(len(self.scale)):    
            ref = input
            if self.scale[i]!=1:
                ref  = F.interpolate(input, scale_factor=self.scale[i], mode='bicubic')
            #feature transformation function f
            base = self.conv_assembly(ref)
            shape_input = base.shape
            #sampling
            raw_w_i = extract_image_patches(base, ksizes=[kernel, kernel],
                                      strides=[self.stride,self.stride],
                                      rates=[1, 1],
                                      padding='same') # [N, C*k*k, L]
            raw_w_i = raw_w_i.view(shape_input[0], shape_input[1], kernel, kernel, -1)
            raw_w_i = raw_w_i.permute(0, 4, 1, 2, 3)    # raw_shape: [N, L, C, k, k]
            raw_w_i_groups = torch.split(raw_w_i, 1, dim=0)
            raw_w.append(raw_w_i_groups)

            #feature transformation function g
            ref_i = self.conv_match(ref)
            shape_ref = ref_i.shape
            #sampling
            w_i = extract_image_patches(ref_i, ksizes=[self.ksize, self.ksize],
                                  strides=[self.stride, self.stride],
                                  rates=[1, 1],
                                  padding='same')
            w_i = w_i.view(shape_ref[0], shape_ref[1], self.ksize, self.ksize, -1)
            w_i = w_i.permute(0, 4, 1, 2, 3)    # w shape: [N, L, C, k, k]
            w_i_groups = torch.split(w_i, 1, dim=0)
            w.append(w_i_groups)

        y = []
        for idx, xi in enumerate(input_groups):
            #group in a filter
            wi = torch.cat([w[i][idx][0] for i in range(len(self.scale))],dim=0)  # [L, C, k, k]
            #normalize
            max_wi = torch.max(torch.sqrt(reduce_sum(torch.pow(wi, 2),
                                                     axis=[1, 2, 3],
                                                     keepdim=True)),
                               self.escape_NaN)
            wi_normed = wi/ max_wi
            #matching
            xi = same_padding(xi, [self.ksize, self.ksize], [1, 1], [1, 1])  # xi: 1*c*H*W
            yi = F.conv2d(xi, wi_normed, stride=1)   # [1, L, H, W] L = shape_ref[2]*shape_ref[3]
            yi = yi.view(1,wi.shape[0], shape_base[2], shape_base[3])  # (B=1, C=32*32, H=32, W=32)
            # softmax matching score
            yi = F.softmax(yi*self.softmax_scale, dim=1)
            
            if self.average == False:
                yi = (yi == yi.max(dim=1,keepdim=True)[0]).float()
            
            # deconv for patch pasting
            raw_wi = torch.cat([raw_w[i][idx][0] for i in range(len(self.scale))],dim=0)
            yi = F.conv_transpose2d(yi, raw_wi, stride=self.stride,padding=1)/4.
            y.append(yi)
      
        y = torch.cat(y, dim=0)+res*self.res_scale  # back to the mini-batch
        return y

5.实验

  对于金字塔注意力模块，作者设置比例因子为S={1,0.9,0.8,0.7,0.6}构建了一个5级的特征金字塔，通过双三次插值来对特征图进行下采样，所提出的 PANet 包含80个 residual blocks。在第四十个后插入一个金字塔注意力模块，所有特征都为64通道（在 embeded gaussian 中的通道数量减少为32）。
  在训练阶段，作者选择batch_size为16，利用水平垂直翻转和随机旋转来对训练数据进行增强，optimizer优化器选为adam。初始化学习率lr为$10^{-4}$。
  该方法在图像降噪、去马赛克、去压缩伪影、超分辨率方面都进行了实验，效果都非常不错。具体数据参考论文内容。该文章使用了一个结构简单的 backbone ，然后只加了一个 pyramid attention 模块，就取得了非常好的效果。因此作者认为，该模块可以在以后的图像修复网络中作为基础模块来进行应用。