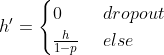跟李沐学AI--Dropout
上一篇学习了怎么利用权重衰退来改善过拟合问题,这一篇讨论用Dropout(暂退法)改善过拟合。
线性模型在求解时,没有考虑特征之间的交互作用。与线性模型不同,深度神经网络不局限于单独查看每个特征,而是学习特征之间的交互。当样本数量足够多时, 线性模型往往不会过拟合,而深度神经网络仍有可能过拟合(我的理解是训练的时候神经网络记住了所有的训练数据,因此在训练时表现良好,损失可以控制在很小的范围。而面对不确定的多变的测试数据时,神经网络又无法得到很好的预测效果。)
为了让模型有更好的”泛化性“,模型在面对扰动时应具有很好的稳健性(即对噪声不敏感)。最简单的方法是给输入添加一些噪声,1995年,克⾥斯托弗·毕晓普证明了具有输⼊噪声的训练等价于Tikhonov正则化。随后,2014年,斯⾥⽡斯塔⽡等⼈提出在网络的层与层之间加入噪声,也就是dropout方法。
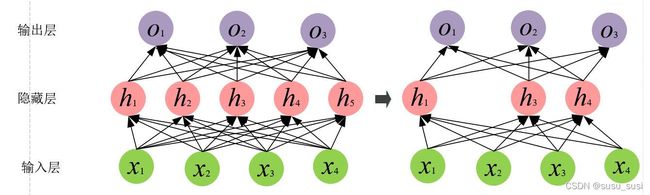
暂退法的思想是在隐藏层中丢弃某些单元,以减少模型对某些特征的依赖。如下图所示:
那么,如何实现神经元的丢弃呢?在标准暂退法正则化中,假设某个神经元被丢弃的概率为p,那么该神经元的输出可以表示为:
计算![]() 期望值:
期望值:
这种插入方式使得在插入了噪声后,每一层的期望等于没有插入噪声时的值。
手动实现暂退法代码如下:
import torch
from torch import nn
from d2l import torch as d2l
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
dropout1, dropout2 = 0.2, 0.5
def dropout_layer(x, dropout):
assert 0 <= dropout <= 1
if dropout == 1:
return torch.zeros_like(x)
if dropout == 0:
return x
# mask = (torch.Tensor(x.shape).uniform_(0, 1) > dropout).float() # 生成0-1之间的均匀分布,大于dropout即为1,小于即为0
mask = (torch.rand(x.shape) > dropout).float()
return mask * x / (1.0 - dropout)
# *************************************** 定义模型 *******************************************************************
class Net(nn.Module):
def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2, is_training=True):
super(Net, self).__init__()
self.num_inputs = num_inputs
self.training = is_training
self.lin1 = nn.Linear(num_inputs, num_hiddens1)
self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
self.lin3 = nn.Linear(num_hiddens2, num_outputs)
self.relu = nn.ReLU()
def forward(self, x):
H1 = self.relu(self.lin1(x.reshape((-1, self.num_inputs))))
# 在训练时使用dropout
if self.training: # == True:
H1 = dropout_layer(H1, dropout1)
H2 = self.relu(self.lin2(H1))
if self.training:
H2 = dropout_layer(H2, dropout2)
out = self.lin3(H2)
return out
# *************************************** 训练和测试 *******************************************************************
def train():
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.plt.show()
if __name__ == "__main__":
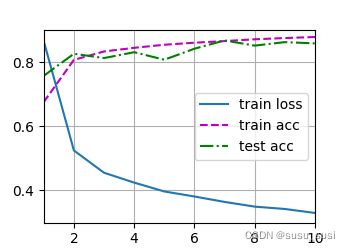
train()运行结果如下:
简洁实现:
import torch
from torch import nn
from d2l import torch as d2l
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.1)
def train():
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256 # 定义两个隐藏层,每个隐藏层都包含256个单元
dropout1, dropout2 = 0.2, 0.5 # 隐藏层丢弃的概率
net = nn.Sequential(nn.Flatten(), nn.Linear(num_inputs, num_hiddens1), nn.ReLU(), nn.Dropout(dropout1),
nn.Linear(num_hiddens1, num_hiddens2), nn.ReLU(), nn.Dropout(dropout2), nn.Linear(num_hiddens2, num_outputs))
net.apply(init_weights)
num_epochs, lr, batch_size = 10, 0.5, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss(reduction='none')
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.plt.show()
if __name__ == "__main__":
train()