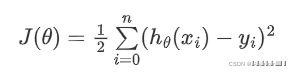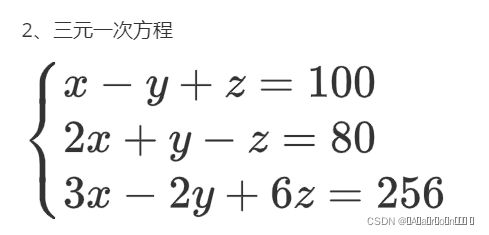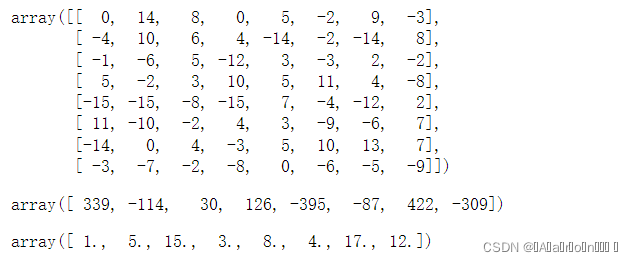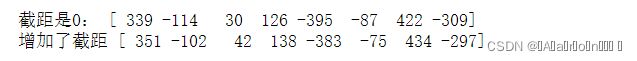机器学习2-正规方程的学习
目录
一、最小二乘法矩阵表示:
二、多元一次方程举例:
1、二元一次方程
1、用线性代数解法:
2、用正规方程解法:
2、三元一次方程
正规方程解法:
3、八元一次方程
1、正规方程解法:
2、sklearn算法解正规方程:
一、最小二乘法矩阵表示:
最小二乘法可以将误差方程转化为有确定解的代数方程组(其方程式数目正好等于未知数的个数),从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。公式如下:
公式是如何推导的?
 二、多元一次方程举例:
二、多元一次方程举例:
先导包:
import numpy as np
import matplotlib.pyplot as plt
# linear线性,model模型、算法
# LinearRegression:线性回归
from sklearn.linear_model import LinearRegression1、二元一次方程
1、用线性代数解法:
X = np.array([[1,1],[2,-1]])
Xy = np.array([14,10])
y ![]()
# linalg 线性代数,slove计算线性回归问题
np.linalg.solve(X,y) 2、用正规方程解法:
A = X.T.dot(X)
# 逆矩阵
B = np.linalg.inv(A)
# 向量点乘运算
C = B.dot(X.T)
C.dot(y)2、三元一次方程
正规方程解法:
X = np.array([[1,-1,1],[2,1,-1],[3,-2,6]])
y = np.array([100,80,256])
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)3、八元一次方程
1、正规方程解法:
# 上面八元一次方程对应的X数据
X = np.array([[ 0 ,14 , 8 , 0 , 5, -2, 9, -3],
[ -4 , 10 , 6 , 4 ,-14 , -2 ,-14 , 8],
[ -1 , -6 , 5 ,-12 , 3 , -3 , 2 , -2],
[ 5 , -2 , 3 , 10 , 5 , 11 , 4 ,-8],
[-15 ,-15 ,-8 ,-15 , 7 , -4, -12 , 2],
[ 11 ,-10 , -2 , 4 , 3 , -9 , -6 , 7],
[-14 , 0 , 4 , -3 , 5 , 10 , 13 , 7],
[ -3 , -7 , -2 , -8 , 0 , -6 , -5 , -9]])
# 对应的y
y = np.array([ 339 ,-114 , 30 , 126, -395 , -87 , 422, -309])
display(X,y)# 正规方程
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
w2、sklearn算法解正规方程:
# fit_intercept = False 不计算截距!!!
model = LinearRegression(fit_intercept = False)
# X 数据;y 目标值
# X ---> y
# 查看X,y
display(X,y)
# 计算结果
model.fit(X,y)
# coef_ 结果,返回值
# 系数,斜率,W,方程的解
model.coef_# 默认计算截距
model.intercept_如果我们fit_intercept=False中的False改成True,要让它计算截距怎么办呢?
我们需要自行增加截距!我设截距为12.
# 设截距是12
# 目标值进行移动,向上移动,加法运算
print('截距是0:',y)
y += 12
print('增加了截距',y)其中b是一个未知变量,需要进行方程求解。我们可以把b看做w0*1。
这样我们可以对每一个方程新增加一列1:
# 向其后面增加一列
X = np.concatenate([X,np.full(shape = (8,1),fill_value=1)],axis = 1)
X正规方程求解:
np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)sklearn算法求解:
model = LinearRegression(fit_intercept=False)
model.fit(X,y)
display(model.coef_,model.intercept_)从两种方法求解的结果可知,结果并不是正确的。什么原因呢?
我们先看看X的形状:
X.shape原因如下:8代表8个方程,9代表计算的未知数。当我们增加了新的一列,意味着未知数都增加了一个,但是方程个数没有增加。即8个9元1次方程,没有固定解,我们还需要增加一个新的方程变成9个9元1次方程,这样才有唯一解!!!
增加一个方程:
# 第9个方程
X9 = np.random.randint(-15,15,size = 8)
X9![]()
# 标准答案
w = np.array([ 1., 5., 15., 3., 8., 4., 17., 12.])
# 上面的8个方程,都有截距是12,第九个方程也一样
X9.dot(w) + 12
y = np.concatenate([y,[X9.dot(w) + 12]])
y![]()
# 第9个方程增加一列1
X9 = np.concatenate([X9,[1]])
X9![]()
# 将第九个方程和前面八个方程合并
X = np.concatenate([X,[X9]])
X先用正规方程求解9个9元1次方程是否正确:
np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)![]()
从结果可知,是正确的!然后我们用sklearn算法试试:
计算截距时:
# 四舍五入,截距:12
model = LinearRegression(fit_intercept=True)
model.fit(X,y)
display(model.coef_,model.intercept_)从结果可知,array中有个0,这怎么理解呢?
我们可以理解成权重,0代表的是没有权重,意思是我们在计算截距的时候,w0是我们自己假设出来的(因为在原方程中并没有截距),sklearn最终在计算的时候,把他理解成0权重了。而计算出的截距为11.999999时,我们自动四舍五入就好了。而计算出的截距为11.999999时,我们自动四舍五入就好了。
未计算截距时:
model = LinearRegression(fit_intercept=False)
model.fit(X,y)
display(model.coef_,model.intercept_)从计算结果可知结果是正确的!
当我们把截距去掉时,变成9个8元一次方程时,再计算截距再来看看结果:
我们先看看X是怎样的:
X去掉1后:
# [:-x] 表示 除了最后 x 个元素构成的切片
# [-x:] 表示 最后 x 个元素构成的切片
X[:,:-1]
# 四舍五入,截距:12
model = LinearRegression(fit_intercept=True)
# 截距去掉!
model.fit(X[:,:-1],y)
display(model.coef_,model.intercept_)从结果可知,array中只有8位,截距为11.99999999,四舍五入进为12就好了。