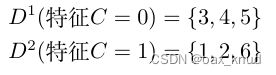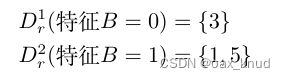机器学习与数据挖掘实验二:以信息增益为划分准则构造决策树【例题求解】
系列文章目录
机器学习与数据挖掘实验一:牛顿法,梯度下降实现对数几率回归【详细原理+python代码】
机器学习与数据挖掘实验二:以信息增益为划分准则构造决策树【例题求解】
机器学习与数据挖掘实验三:基于 CNN (VGG,GoogLeNet)的海面舰船图像分类【详细原理+python代码】
机器学习与数据挖掘实验四:基于特征工程的支持向量机分类实验【详细原理+python代码】
文章目录
- 系列文章目录
- 一、问题重述
- 二、解答
-
- 2.1 根节点属性划分
-
- 2.1.1 特征A信息增益计算
- 2.1.2 特征B信息增益计算
- 2.1.3 特征C信息增益计算
- 2.2 左孩子节点属性划分
-
- 2.2.1 特征B信息增益计算
- 2.2.2 特征C信息增益计算
- 2.3 右孩子节点属性划分
-
- 2.3.1 特征B信息增益计算
- 2.3.2 特征C信息增益计算
一、问题重述
考虑下面的训练集:共计6个训练样本,每个训练样本有三个维度的特征属性和标记信息。详细信息如表1所示。
请通过训练集中的数据训练一棵决策树,要求通过“信息增益”(information gain)为准则来选择划分属性。给出详细的计算过程并画出最终的决策树。
| 序号 | 特征A | 特征B | 特征C | 标记 |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 1 | 0 | 1 | 1 |
二、解答
由题意,该数据集包含6个训练样本,类别有2个,因此得到初始化条件划分类别个数 ∣ Y ∣ = 2 |\mathcal{Y}|=2 ∣Y∣=2,数据集D表示如下:
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , ( x 4 , y 4 ) , ( x 5 , y 5 ) , ( x 6 , y 6 ) } \begin{aligned} D=&\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right),\left(x_{4}, y_{4}\right),\left(x_{5}, y_{5}\right),\left(x_{6}, y_{6}\right)\right\} \end{aligned} D={(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),(x6,y6)}
D表示根节点包含的样本。其中, x i x_i xi表示样本i的特征向量, y i y_i yi表示样本标签,由此开始构造决策树。
2.1 根节点属性划分
在决策树开始时,根节点包含所有样本,其中正例占 p 1 = 1 2 p_{1}=\frac{1}{2} p1=21,反例占 p 2 = 1 2 p_{2}=\frac{1}{2} p2=21,计算根节点的信息熵为:
Ent ( D ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 2 log 2 1 2 + 1 2 log 2 1 2 ) = 1 \begin{aligned} \operatorname{Ent}(D) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{2} \log_{2} \frac{1}{2}+\frac{1}{2} \log_{2} \frac{1}{2}\right) &=1 \end{aligned} Ent(D)=−i=1∑2pilog2pi=−(21log221+21log221)=1
当前属性集为{特征A,特征B,特征C},接下来计算每个属性的信息增益。
2.1.1 特征A信息增益计算
使用特征A对D进行划分得到对应两个数据子集分别为:

对于 D 1 = { 1 , 3 , 5 } D^{1}=\{1,3,5\} D1={1,3,5},其中正例占 p 1 = 1 3 p_{1}=\frac{1}{3} p1=31,反例占 p 2 = 2 3 p_{2}=\frac{2}{3} p2=32,因此,根节点在特征A上的第一个分支节点信息熵为 :
Ent ( D 1 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 3 log 2 1 3 + 2 3 log 2 2 3 ) = 0.918 \begin{aligned} \operatorname{Ent}( D^{1}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{3} \log_{2} \frac{1}{3}+\frac{2}{3} \log_{2} \frac{2}{3}\right) &=0.918 \end{aligned} Ent(D1)=−i=1∑2pilog2pi=−(31log231+32log232)=0.918
对于 D 2 = { 2 , 4 , 6 } D^{2}=\{2,4,6\} D2={2,4,6},其中正例占 p 1 = 2 3 p_{1}=\frac{2}{3} p1=32,反例占 p 2 = 1 3 p_{2}=\frac{1}{3} p2=31,因此,根节点在特征A上第二个分支节点信息熵为 :
Ent ( D 2 ) = − ∑ i = 1 2 p i log 2 p i = − ( 2 3 log 2 2 3 + 1 3 log 2 1 3 ) = 0.918 \begin{aligned} \operatorname{Ent}( D^{2}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{2}{3} \log_{2} \frac{2}{3}+\frac{1}{3} \log_{2} \frac{1}{3}\right) &=0.918 \end{aligned} Ent(D2)=−i=1∑2pilog2pi=−(32log232+31log231)=0.918
综上,特征A的信息增益为:
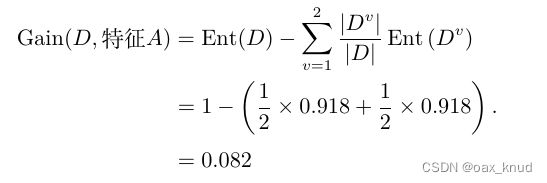
2.1.2 特征B信息增益计算
使用特征B对D进行划分得到对应两个数据子集分别为:
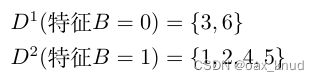
对于 D 1 = { 3 , 6 } D^{1}=\{3,6\} D1={3,6},其中正例占 p 1 = 1 2 p_{1}=\frac{1}{2} p1=21,反例占 p 2 = 1 2 p_{2}=\frac{1}{2} p2=21,因此,根节点在特征B上第一个分支节点信息熵为 :
Ent ( D 1 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 2 log 2 1 2 + 1 2 log 2 1 2 ) = 1 \begin{aligned} \operatorname{Ent}( D^{1}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{2} \log_{2} \frac{1}{2}+\frac{1}{2} \log_{2} \frac{1}{2}\right) &=1 \end{aligned} Ent(D1)=−i=1∑2pilog2pi=−(21log221+21log221)=1
对于 D 2 = { 1 , 2 , 4 , 5 } D^{2}=\{1,2,4,5\} D2={1,2,4,5},其中正例占 p 1 = 1 2 p_{1}=\frac{1}{2} p1=21,反例占 p 2 = 1 2 p_{2}=\frac{1}{2} p2=21,因此,根节点在特征B上第二个分支节点信息熵为 :
Ent ( D 2 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 2 log 2 1 2 + 1 2 log 2 1 2 ) = 1 \begin{aligned} \operatorname{Ent}( D^{2}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{2} \log_{2} \frac{1}{2}+\frac{1}{2} \log_{2} \frac{1}{2}\right) &=1 \end{aligned} Ent(D2)=−i=1∑2pilog2pi=−(21log221+21log221)=1
因此,特征B的信息增益为:
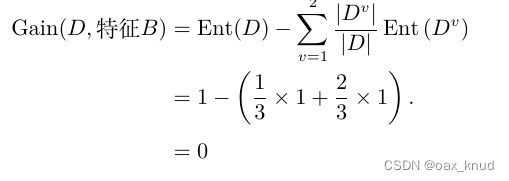
2.1.3 特征C信息增益计算
对于 D 1 = { 3 , 4 , 5 } D^{1}=\{3,4,5\} D1={3,4,5},其中正例占 p 1 = 2 3 p_{1}=\frac{2}{3} p1=32,反例占 p 2 = 1 3 p_{2}=\frac{1}{3} p2=31,因此,根节点在特征C上第一个分支节点的信息熵为 :
Ent ( D 1 ) = − ∑ i = 1 2 p i log 2 p i = − ( 2 3 log 2 2 3 + 1 3 log 2 1 3 ) = 0.918 \begin{aligned} \operatorname{Ent}( D^{1}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{2}{3} \log_{2} \frac{2}{3}+\frac{1}{3} \log_{2} \frac{1}{3}\right) &=0.918 \end{aligned} Ent(D1)=−i=1∑2pilog2pi=−(32log232+31log231)=0.918
对于 D 2 = { 1 , 2 , 6 } D^{2}=\{1,2,6\} D2={1,2,6},其中正例占 p 1 = 1 3 p_{1}=\frac{1}{3} p1=31,反例占 p 2 = 2 3 p_{2}=\frac{2}{3} p2=32,因此,根节点在特征C上第二个分支节点的信息熵为 :
Ent ( D 2 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 3 log 2 1 3 + 2 3 log 2 2 3 ) = 0.918 \begin{aligned} \operatorname{Ent}( D^{2}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{3} \log_{2} \frac{1}{3}+\frac{2}{3} \log_{2} \frac{2}{3}\right) &=0.918 \end{aligned} Ent(D2)=−i=1∑2pilog2pi=−(31log231+32log232)=0.918
因此,特征C的信息增益为:
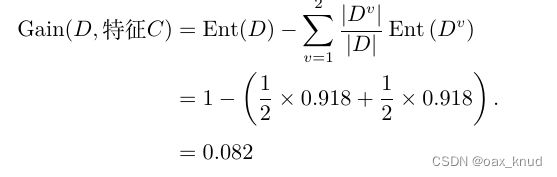
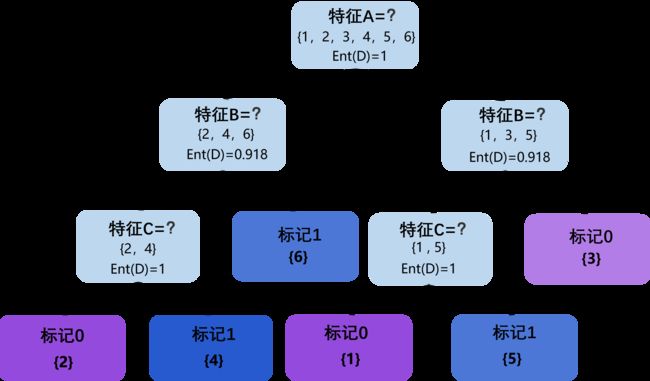
因此,可以得到根节点的属性划分中,特征A和特征C的信息增益相同且均为最大。在这里,选择特征A作为根节点的属性划分特征,根节点的决策树如图所示。
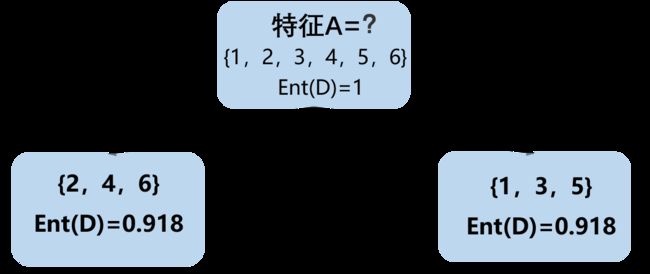
2.2 左孩子节点属性划分
在决策树的根节点划分后开,分别对决策树的左右孩子节点进行划分。其中,左孩子节点包含样本数据集 D l = { 2 , 4 , 6 } D_l=\{2,4,6\} Dl={2,4,6}其中正例占 p 1 = 2 3 p_{1}=\frac{2}{3} p1=32,反例占 p 2 = 1 3 p_{2}=\frac{1}{3} p2=31,计算左孩子节点的信息熵为:
Ent ( D l ) = − ∑ i = 1 2 p i log 2 p i = − ( 2 3 log 2 2 3 + 1 3 log 2 1 3 ) = 0.918 \begin{aligned} \operatorname{Ent}(D_l) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{2}{3} \log_{2} \frac{2}{3}+\frac{1}{3} \log_{2} \frac{1}{3}\right) &=0.918 \end{aligned} Ent(Dl)=−i=1∑2pilog2pi=−(32log232+31log231)=0.918
当前属性集去除特征A后变化为{特征B,特征C},接下来计算每个属性的信息增益。
2.2.1 特征B信息增益计算
使用特征B对 D l D_l Dl进行划分得到对应两个数据子集分别为:

对于 D l 1 = { 6 } D_l^{1}=\{6\} Dl1={6},其中正例占 p 1 = 1 p_{1}=1 p1=1,因此,左孩子节点在特征B上第一个分支节点的信息熵为 :
E n t ( D l 1 ) = p 1 log 2 p 1 = 1 × log 2 1 = 0 Ent\left(D_{l}^{1}\right)=p_{1} \log _{2} p_{1}=1 \times \log _{2} 1=0 Ent(Dl1)=p1log2p1=1×log21=0
对于 D l 2 = { 2 , 4 } D_l^{2}=\{2,4\} Dl2={2,4},其中正例占 p 1 = 1 2 p_{1}=\frac{1}{2} p1=21,反例占 p 2 = 1 2 p_{2}=\frac{1}{2} p2=21,因此,左孩子节点在特征B上第二个 分支节点的信息熵为 :
Ent ( D l 2 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 2 log 2 1 2 + 1 2 log 2 1 2 ) = 1 \begin{aligned} \operatorname{Ent}( D_l^{2}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{2} \log_{2} \frac{1}{2}+\frac{1}{2} \log_{2} \frac{1}{2}\right) &=1 \end{aligned} Ent(Dl2)=−i=1∑2pilog2pi=−(21log221+21log221)=1
因此,特征B的信息增益为:
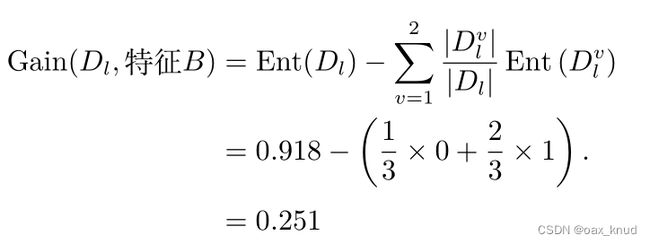
2.2.2 特征C信息增益计算
使用特征C对 D l D_l Dl进行划分得到对应两个数据子集分别为:
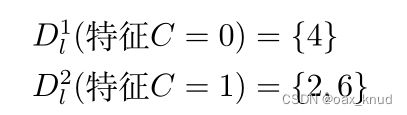
对于 D l 1 = { 4 } D_l^{1}=\{4\} Dl1={4},其中正例占 p 1 = 1 p_{1}=1 p1=1,因此,左孩子第一个分支节点的信息熵为 :
E n t ( D l 1 ) = p 1 log 2 p 1 = 1 × log 2 1 = 0 Ent\left(D_{l}^{1}\right)=p_{1} \log _{2} p_{1}=1 \times \log _{2} 1=0 Ent(Dl1)=p1log2p1=1×log21=0
对于 D l 2 = { 2 , 6 } D_l^{2}=\{2,6\} Dl2={2,6},其中正例占 p 1 = 1 2 p_{1}=\frac{1}{2} p1=21,反例占 p 2 = 1 2 p_{2}=\frac{1}{2} p2=21,因此,左孩子第二个分支节点的信息熵为 :
Ent ( D l 2 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 2 log 2 1 2 + 1 2 log 2 1 2 ) = 1 \begin{aligned} \operatorname{Ent}( D_l^{2}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{2} \log_{2} \frac{1}{2}+\frac{1}{2} \log_{2} \frac{1}{2}\right) &=1 \end{aligned} Ent(Dl2)=−i=1∑2pilog2pi=−(21log221+21log221)=1
因此,特征C的信息增益为:、
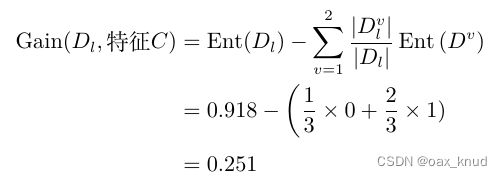
因此,可以得到左孩子节点的属性划分中,特征B的信息增益最大。左孩子节点的决策树属性划分如图所示。

通过ID3算法可知,在左孩子节点属性划分后,其属性集仅剩下特征C,因此,对于左孩子节点的左孩子节点,按照特征C继续划分,可以得到左孩子节点最终决策树如图

2.3 右孩子节点属性划分
根节点划分后,右孩子节点包含样本数据集 D r = { 1 , 3 , 5 } D_r=\{1,3,5\} Dr={1,3,5}其中正例占 p 1 = 1 3 p_{1}=\frac{1}{3} p1=31,反例占 p 2 = 2 3 p_{2}=\frac{2}{3} p2=32,计算右孩子节点的信息熵为:
Ent ( D r ) = − ∑ i = 1 2 p i log 2 p i = − ( 2 3 log 2 2 3 + 1 3 log 2 1 3 ) = 0.918 \begin{aligned} \operatorname{Ent}(D_r) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{2}{3} \log_{2} \frac{2}{3}+\frac{1}{3} \log_{2} \frac{1}{3}\right) &=0.918 \end{aligned} Ent(Dr)=−i=1∑2pilog2pi=−(32log232+31log231)=0.918
计算当前属性集为{特征B,特征C}中每个属性的信息增益如下。
2.3.1 特征B信息增益计算
使用特征B对 D r D_r Dr进行划分得到对应两个数据子集分别为:
对于 D r 1 = { 3 } D_r^{1}=\{3\} Dr1={3},其中反例占 p 1 = 1 p_{1}=1 p1=1,因此,右孩子节点在特征B上第一个分支节点的信息熵为 :
E n t ( D r 1 ) = p 1 log 2 p 1 = 1 × log 2 1 = 0 Ent\left(D_{r}^{1}\right)=p_{1} \log _{2} p_{1}=1 \times \log _{2} 1=0 Ent(Dr1)=p1log2p1=1×log21=0
对于 D r 2 = { 1 , 5 } D_r^{2}=\{1,5\} Dr2={1,5},其中正例占 p 1 = 1 2 p_{1}=\frac{1}{2} p1=21,反例占 p 2 = 1 2 p_{2}=\frac{1}{2} p2=21,因此,对于右孩子节点在特征B上第二个分支节点的信息熵为 :
Ent ( D l 2 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 2 log 2 1 2 + 1 2 log 2 1 2 ) = 1 \begin{aligned} \operatorname{Ent}( D_l^{2}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{2} \log_{2} \frac{1}{2}+\frac{1}{2} \log_{2} \frac{1}{2}\right) &=1 \end{aligned} Ent(Dl2)=−i=1∑2pilog2pi=−(21log221+21log221)=1
因此,特征B的信息增益为:

2.3.2 特征C信息增益计算
使用特征C对 D r D_r Dr进行划分得到对应两个数据子集分别为:
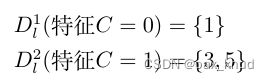
对于 D r 1 = { 1 } D_r^{1}=\{1\} Dr1={1},其中反例占 p 1 = 1 p_{1}=1 p1=1,因此,右孩子节点在特征C上第一个分支节点的信息熵为 :
E n t ( D r 1 ) = p 1 log 2 p 1 = 1 × log 2 1 = 0 Ent\left(D_{r}^{1}\right)=p_{1} \log _{2} p_{1}=1 \times \log _{2} 1=0 Ent(Dr1)=p1log2p1=1×log21=0
对于 D r 2 = { 1 , 5 } D_r^{2}=\{1,5\} Dr2={1,5},其中正例占 p 1 = 1 2 p_{1}=\frac{1}{2} p1=21,反例占 p 2 = 1 2 p_{2}=\frac{1}{2} p2=21,因此,右孩子节点在特征C上第二个分支节点的信息熵为:
Ent ( D l 2 ) = − ∑ i = 1 2 p i log 2 p i = − ( 1 2 log 2 1 2 + 1 2 log 2 1 2 ) = 1 \begin{aligned} \operatorname{Ent}( D_l^{2}) &=-\sum_{i=1}^{2} p_{i} \log_{2} p_{i} &=-\left(\frac{1}{2} \log_{2} \frac{1}{2}+\frac{1}{2} \log_{2} \frac{1}{2}\right) &=1 \end{aligned} Ent(Dl2)=−i=1∑2pilog2pi=−(21log221+21log221)=1
因此,特征C的信息增益为:
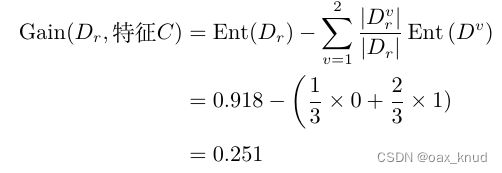
因此,可以得到右孩子节点的属性划分中,特征B和特征C的息增益相同且均为最大。在这里,选择特征B作为右孩子节点的属性划分特征,右孩子节点决策树如图所示。
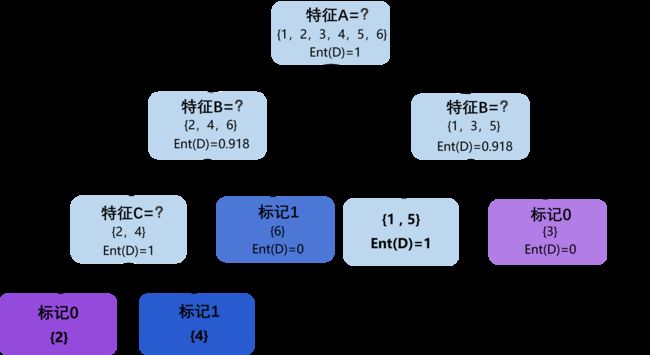
通过ID3算法可知,在右孩子节点属性划分后,其属性集仅剩下特征C,因此,对于右孩子节点的左孩子节点,按照特征C继续划分右孩子节点,可以得到最终决策树如图。