Deep Learning 记录：预测房价——回归问题（House Prices - Advanced Regression Techniques）

---

一、环境配置说明

1.使用Anaconda作为python环境管理

使用Anaconda作为python环境管理，用于配置对应的虚拟环境

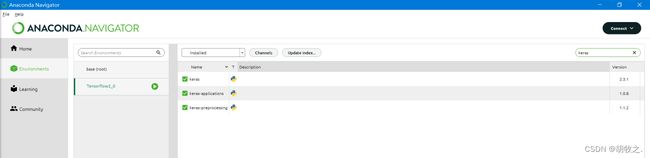
2.虚拟环境介绍

采用2.3.1版本的Keras与2.0.0版本的tensorflow

因为keras与tensorflow两者存在版本匹配，否则将因不兼容而报错。

---

二、数据集介绍与可视化展示

1.数据集介绍

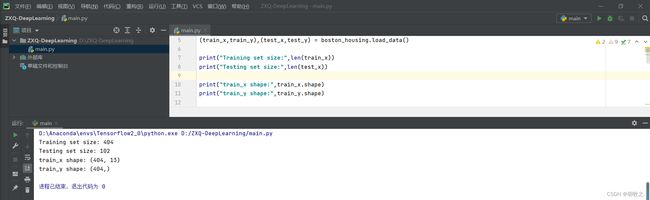
采用的数据集是从keras中导入的波士顿房价数据集，共506个样本。
每个样本含13个数值特征和1个房价平均值。
load_data()默认test_split为0.2，故划分出404个训练样本和102个测试样本。

2.可视化展示

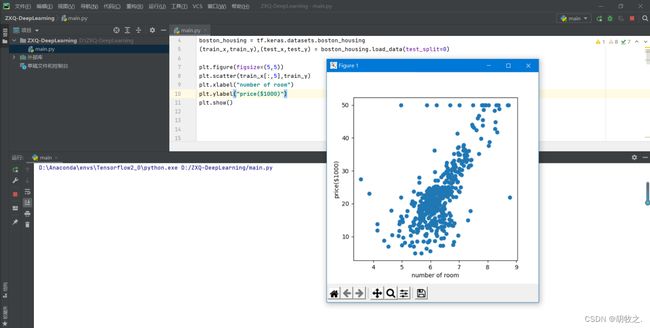
未说明横纵坐标的全部情况展示：

在13个数值特征中，我们选择第6个数值特征房间数作为横坐标，纵坐标为房屋价格（以$1000作为单位），以此进行具体展示:

---

三、数据处理与说明

1.数据标准化的目的

将取值较大的数或异质数据输入到神经网络中并不安全，可能导致较大的梯度更新，进而导致网络无法收敛。

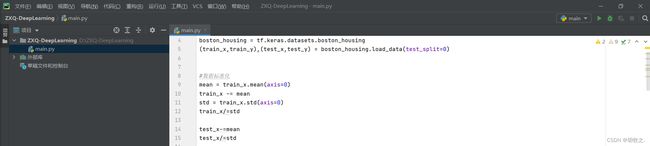
2.标准化具体实现

为了保证测试结果的真实可靠，我们不能泄露测试集的信息，所以测试数据集的标准化依然是采用由训练数据集计算出来的均值和标准差。

---

四、网络构建与说明

1.网络选择

利用Sequential类定义模型，层线性堆叠
根据资料得知，带relu激活的全连接层(Dense)的简单堆叠在处理简单的向量数据上有出色的表现，所以采用Dense层堆叠

2.参数说明

以第一层为例，此时对应参数分别为隐藏单元个数、激活函数类型和输入矩阵数据第1轴要求
每个带有relu激活的Dense层都实现了：output = relu(dot(w, input) + b)
w为权重矩阵，b为偏置向量

w形状为（输入矩阵第1轴，隐藏单元个数）
b为向量，故需要通过广播实现形状不同的张量相加

隐藏单元数目越多，网络越能学习到更加复杂的表示，但可能导致过拟合
激活函数用于扩展假设空间，充分利用多层表示的优势
输入矩阵第1轴要求仅在第一层出现，之后添加的层都会自动匹配输入层的形状

3.损失函数与优化器选择

损失函数，衡量当前任务是否成功完成，对于回归问题，我们选择mes损失函数，即均方误差，表示预测值与目标值之差的平方。

优化器，决定如何基于损失函数对网络进行更新，对于当前问题，我们选择rmsprop优化器（均方根反向传播）。

评价指标，用于判断模型的性能，但不用于网络参数的更新，对于当前问题，我们选择mae，即平均绝对误差，表示预测值与目标值之差的绝对值。

---

五、小样本的K折验证

1.直接交叉验证的局限性

总共只有404个训练样本，如果直接依照交叉验证的思路将其划分为训练集和验证集，不同的划分方式将导致验证分数有很大的差异，
无法对模型进行可靠的评估。

2.K折验证说明

K折交叉验证，将数据划分为K个分区，总共要计算K轮，将计算出的K个验证分数的平均值作为模型的验证分数，每个分区轮流作为一个验证集，
剩下的K-1个分区作为训练集。

3.代码具体实现与说明

（一）参数选择

 K选择4，即将划分为4个分区，并计算出4个验证分数以其平均值作为验证分数。
 num_val_samples表示分区大小
 num_epochs表示训练的轮数
 all_mae_histories存储每一轮的验证分数

（二）分区

 根据参数i选择分区担任验证集，其余的k-1个分区作为训练集
 np.concatenate()，功能是根据给定的axis参数，将两个张量进行合并，但要求剩下的部分要可以对应，否则不能合并。
 在当前划分中，就是将两个训练集合并为一个训练集。

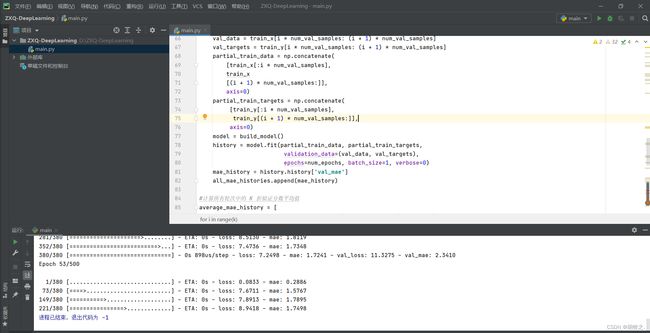
（三）静默训练

history是调用model.fit()后返回的一个History对象，是一个字典，包含着训练过程中的所有数据
model.fit()是拟合，值得注意的是此时verbose为0，静默模式，也就是不标准输出流中输出日志信息

以下为verbose参数为1时的运行截图：

---

六、验证图像绘制与超参数选择

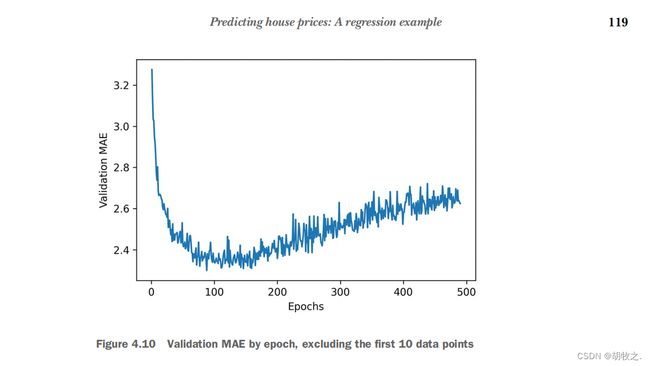
1.验证图像绘制与比对

2.图像分析与epochs选择

第一版中epochs选择为80，第二版中为130，在本地运行中，我测试了多次，但测试的验证mae在35轮与68轮均出现了相近的最低点，
由于两者相差较大，取35可能导致训练不够，取68可能导致过拟合，所以我折中选择了52作为最终的epochs

3.分批次训练的目的

批次大小是一个超参数，表示在更新内部模型参数之前要处理的样本数

分批次可以更好地概括学习，如果不分批次，网络将一次性传播，会使网络对每个样本过于敏感，也就降低了模型的泛化能力

---

七、训练最终模型

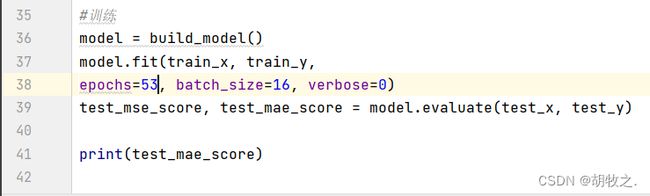
1.运行代码展示

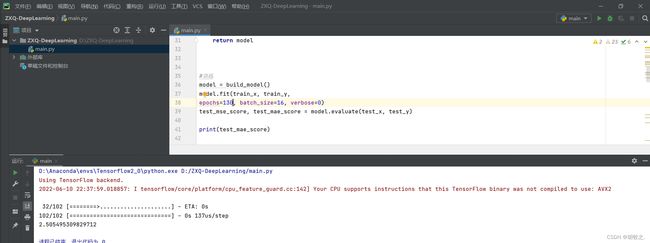
2.运行结果展示

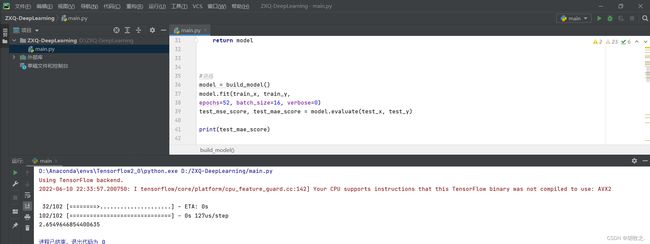
第一版结果：

第二版结果：

所得结果与课本示例仍有着1000$左右的差距

3.适当调参

将epochs修改为130，所得结果与第二版课本相差不大

---

八、代码

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
boston_housing = tf.keras.datasets.boston_housing
(train_x,train_y),(test_x,test_y) = boston_housing.load_data(test_split=0.2)


#数据标准化
mean = train_x.mean(axis=0)
train_x -= mean
std = train_x.std(axis=0)
train_x/=std

test_x-=mean
test_x/=std




#构建网络
from keras import models
from keras import layers

def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu',
    input_shape=(train_x.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model



#训练
model = build_model()
model.fit(train_x, train_y,
epochs=130, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_x, test_y)

print(test_mae_score)

#K折验证
# import numpy as np
# k = 4
# num_val_samples = len(train_x) // k
# # num_epochs = 100
# all_scores = []
# for i in range(k):
#  print('processing fold #', i)
#  val_data = train_x[i * num_val_samples: (i + 1) * num_val_samples]
#  val_targets = train_y[i * num_val_samples: (i + 1) * num_val_samples]
#  partial_train_data = np.concatenate(
#  [train_x[:i * num_val_samples],
#  train_x[(i + 1) * num_val_samples:]],
#  axis=0)
#  partial_train_targets = np.concatenate(
#  [train_y[:i * num_val_samples],
#  train_y[(i + 1) * num_val_samples:]],
#  axis=0)
#  model = build_model()
#  model.fit(partial_train_data, partial_train_targets,
#  epochs=num_epochs, batch_size=1, verbose=0)
#  val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
#  all_scores.append(val_mae)

# 保存每折的验证结果
# import numpy as np
# k = 4
# num_val_samples = len(train_x) // k
# num_epochs = 500
# all_mae_histories = []
# for i in range(k):
#     print('processing fold #', i)
#     val_data = train_x[i * num_val_samples: (i + 1) * num_val_samples]
#     val_targets = train_y[i * num_val_samples: (i + 1) * num_val_samples]
#     partial_train_data = np.concatenate(
#         [train_x[:i * num_val_samples],
#         train_x
#         [(i + 1) * num_val_samples:]],
#         axis=0)
#     partial_train_targets = np.concatenate(
#          [train_y[:i * num_val_samples],
#           train_y[(i + 1) * num_val_samples:]],
#          axis=0)
#     model = build_model()
#     history = model.fit(partial_train_data, partial_train_targets,
#                          validation_data=(val_data, val_targets),
#                          epochs=num_epochs, batch_size=1, verbose=0)
#     mae_history = history.history['val_mae']
#     all_mae_histories.append(mae_history)

#计算所有轮次中的 K 折验证分数平均值
# average_mae_history = [
#  np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

#绘制验证分数
# import matplotlib.pyplot as plt
# plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
# plt.xlabel('Epochs')
# plt.ylabel('Validation MAE')
# plt.show()

#删除前十个数据点后绘制验证分数
# def smooth_curve(points, factor=0.9):
#  smoothed_points = []
#  for point in points:
#     if smoothed_points:
#         previous = smoothed_points[-1]
#         smoothed_points.append(previous * factor + point * (1 - factor))
#     else:
#         smoothed_points.append(point)
#  return smoothed_points
#
# smooth_mae_history = smooth_curve(average_mae_history[10:])
#
# plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
# plt.xlabel('Epochs')
# plt.ylabel('Validation MAE')
# plt.show()