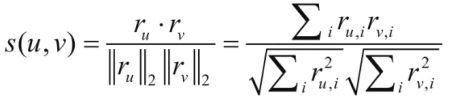推荐算法--协同过滤(user&item)
推荐算法--协同过滤
- 协同过滤简介
-
- 启发式协同过滤算法主要包含 3 个步骤:
- 协同过滤推荐算法优缺点
- 1.基于用户的协同过滤(User-Based)
-
- 1.1 方法步骤
- 1.2 如何选择合适的相似度计算方法
- 1.3计算用户 u 对未评分商品的预测分值
- 1.4通过例子理解
- 1.5代码实现(python)
- 2.基于项目的协同过滤
-
- 2.1 方法步骤:
- 2.2 算法过程
-
- 2.21 建立 物品 — 用户 倒排表
- 2.22 计算items之间的相似度
- 2.23 计算用户对未购买物品的兴趣度
- 2.24理解公式 i∈N(u)∩S(j,K)
- 2.25代码实现(python)
协同过滤简介
我先举一个例子,有一天,你想去看电影了,但你不知道有什么电影好看,然后你可能就会问问你的朋友们,看看有什么好看的电影推荐,这时候大部分人都会倾向于问跟你有品味差不多的人。而这也就是协同过滤的核心思想。
一般来说,协同过滤推荐分为三种类型。第一种是基于用户(user-based)的协同过滤,第二种是基于项目(item-based)的协同过滤,第三种是基于模型(model based)的协同过滤。
协同过滤推荐(Collaborative Filtering recommendation)是在信息过滤和信息系 统中正迅速成为一项很受欢迎的技术。与传统的基于内容过滤直接分析内容进行 推荐不同,协同过滤分析用户兴趣,在用户群中找到指定用户的相似(兴趣)用 户,综合这些相似用户对某一信息的评价,形成系统对该指定用户对此信息的喜 好程度预测。 协同过滤是迄今为止最成功的推荐系统技术,被应用在很多成功的推荐系统中。 电子商务推荐系统可根据其他用户的评论信息,采用协同过滤技术给目标用户推 荐商品。 协同过滤算法主要分为基于启发式和基于模型式两种。 其中,基于启发式的协同过滤算法,又可以分为的协同过滤算法 (User-Based)和基于项目的协同过滤算法(Item-Based)。
启发式协同过滤算法主要包含 3 个步骤:
1)收集用户偏好信息;
2)寻找相似的商品或者用户;
3)产生推荐。
协同过滤推荐算法优缺点
- 算法优点
①能够过滤机器难以自动内容分析的信息,如艺术品,音乐等;
②推荐个性化、自动化程度高、能够有效的利用其他相似用户的回馈信息、加快个性化学习的速度;
③可以帮助用户发现新的兴趣。 - 算法缺点
①稀疏性问题:用户对商品的评价非常稀疏,这样基于用户的评价所得到的用户间的相似性可能不准确;
②随着用户和物品的增多,系统的性能会越来越低;
③对于新用户或者新物品,推荐的质量会较差。
1.基于用户的协同过滤(User-Based)
用相似统计的方法得到具有相似爱好或者兴趣的相邻用户,所以称之为以用户为 基础(User-based)的协同过滤或基于邻居的协同过滤(Neighbor-based Collaborative Filtering)。
简单的说(个人理解):
我逛淘宝用到的应用软件会为我们推荐合适的商品,User-based协同过滤就是通过我们自己过去已买商品以及对于商品喜好程度等信息来和其他用户信息进行对比,若某位用户与我们信息相似度高,则我与该用户称为相似用户,则为我推荐一些该位用户已买或是喜爱的并且我们未买的商品。
1.1 方法步骤
1.收集用户信息 收集可以代表用户兴趣的信息。一般的网站系统使用评分的方式或是给予评价, 这种方式被称为“主动评分”。另外一种是“被动评分”,是根据用户的行为模式由 系统代替用户完成评价,不需要用户直接打分或输入评价数据。电子商务网站在 被动评分的数据获取上有其优势,用户购买的商品记录是相当有用的数据。
2.最近邻搜索(Nearest neighbor search, NNS) 以用户为基础(User-based)的协同过滤的出发点是与用户兴趣爱好相同的另一 组用户,就是计算两个用户的相似度。例如:查找 n 个和 A 有相似兴趣用户,把 他们对 M 的评分作为 A 对 M 的评分预测。一般会根据数据的不同选择不同的算 法,目前较多使用的相似度算法有 Pearson Correlation Coefficient(皮尔逊相关系数)、Cosine-based Similarity(余弦相似度)、Adjusted Cosine Similarity(调整后 的余弦相似度)。
基于用户(User-Based)的协同过滤算法首先要根据用户历史行为信息,寻找与 新用户相似的其他用户;同时,根据这些相似用户对其他项的评价信息预测当前 新用户可能喜欢的项。
1.2 如何选择合适的相似度计算方法
常用的两 种相似度计算方法包括皮尔逊相关系数和余弦相似度等
- U,V表示两位用户
- 表示用户U与用户V之间商品评分的交集
![]()
- 表示U用户对商品评分的平均值
![]()
- 表示V用户对I商品的评分
-如果不理解 具体看实例(我记不住)
1.3计算用户 u 对未评分商品的预测分值
另一个重要的环节就是计算用户u对未评分商品的预测分值。首先根据上一步中的相似度计算,寻找用户u的邻居集N∈U,其中N表示邻居集,U表示用户集。然后,结合用户评分数据集,预测用户u对项i的评分,计算公式如下所示:
- 预测用户u对项i的评分
- 其中 s(u,u’) 表示用户u和用户u’的相似度。(
上面有公式)
1.4通过例子理解
理论和公式都给出,不妨举个实例
假设有如下电子商务评分数据集,预测用户C对商品4的评分。

预测用户C对商品4的评分步骤如下:
(1).寻找C用户的邻居集,
- 从数据集中可以发现,只有用户A和用户D对商品4评过分,因此候选邻居只有2个,分别为用户A和用户D。
- 用户A的平均评分为4,用户C的平均评分为3.667,用户D的平均评分为3
(2).分别计算用户C与邻居集的相似度

根据皮尔逊相关系数公式:
余弦相似度也OK
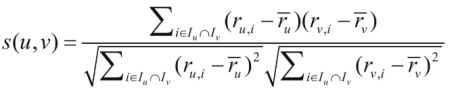
红色区域计算C用户与A用户,用户C和用户A的相似度为:

蓝色区域计算C用户与D 用户的相似度为:
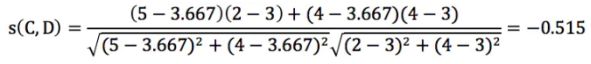
(3).最后直接暴力求C用户对商品4评分预测(公式记不住再上公式 )
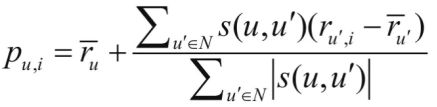

通过以上学习,我们可以发现,基于用户的协同过滤算法就是运用公式计算来预测用户之间相似度以及用户对商品的满意度,最终选择性的推荐给用户商品
1.5代码实现(python)
代码写得比较啰嗦(新手勿喷 ,多指导)
import numpy as np
from math import sqrt
def similarity(ls_1,ls_2,M): #求余弦相似度的函数
fenzi=0#余弦相似度分子
fenmu=0#分母
abs_1=0#分母左边绝对值里的值
abs_2=0#分母右边绝对值里的值
for i in range(M):
fenzi += ls_1[i] * ls_2[i]
abs_1 += pow(ls_1[i],2)
abs_2 += pow(ls_2[i],2)
fenmu=sqrt(abs_1*abs_2)
return fenzi/fenmu#ls_1,ls_2用户相关系数
def forecast(lst_u,R,u_u,M,N,n,m):#求预测评分函数
fenzi=0
fenmu=0
aver_1=0#平均值
aver_2=0
a=0#当前用户购买物品数量
b=0
for i in range(M):
if lst_u[i]!=0:
a+=1
aver_1 +=lst_u[i]
aver_1=aver_1/a
for o in range(N):
if R[o][m]!=0:
for i in range(M):
if R[o][i]!=0:
b+=1
aver_2 +=R[o][i]
aver_2=aver_2/b
fenzi+=u_u[n][o]*(R[o][m]-aver_2)
fenmu+=abs(pex(lst_u,R[o],M))
return aver_1+fenzi/fenmu
R=np.array([[4.,0.,3.,5.],#生成原始矩阵R
[0.,5.,4.,0.],
[5.,4.,2.,0.],
[2.,4.,0.,3.],
[3.,4.,5.,0.]])
print("用户-物品矩阵:")
print(R)
N=len(R)#列长
M=len(R[0])#行长
u_u=np.zeros((N,N))#建立用户与用户之间相关性矩阵u_u
for n in range(N):#建立一个对R的循环筛选未评分item并进行预测评分
for m in range(N):
if n<m:
u_u[n][m]=similarity(R[n],R[m],M)
u_u[m][n]=u_u[n][m]
#将用户相似度小于等于0.6的值归为0(按要求更改阈值)
for n in range(N):
for m in range(N):
if u_u[n][m]<=0.6:
u_u[m][n]=u_u[n][m]=0
print("得到的用户-用户相似度矩阵:")
print(u_u)#打印用户与用户相关系数矩阵
user=['A','B','C','D','E']#用户集合
items=['p1','p2','p3','p4']#商品集合
R_2=R#为了不改变原始矩阵 ,我们复制一个矩阵
for n in range(N):#建立一个对R循环寻找未评分项并且对未评分项进行预测
for m in range(M):
if R[n][m]==0:
R_2[n][m]=forecast(R[n],R,u_u,M,N,n,m)
if R_2[n][m]>4:
print("将商品{:}推荐给用户{:}".format(items[m],user[n]))
print("评分预测矩阵R^:")
print("{:}".format(R_2))
2.基于项目的协同过滤
基于物品的 $ CF $ 的原理和基于用户的 C F CF CF 类似,只是在计算邻居时采用物品本身,而不是从用户的角度,即基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好,推荐相似的物品给他。计算上,就是计算物品之间的相似度,得到物品的相似物品后,根据用户历史的偏好预测当前用户还没有表示偏好的物品,计算得到一个排序的物品列表作为推荐。
2.1 方法步骤:
- 1.收集用户信息
同以用户为基础(User-based)的协同过滤。
- 2.针对项目的最近邻搜索
先计算已评价项目和待预测项目的相似度,并以相似度作为权重,加权各已评价 项目的分数,得到待预测项目的预测值。例如:要对项目 A 和项目 B 进行相 似性计算,要先找出同时对 A 和 B 打过分的组合,对这些组合进行相似度计 算,常用的算法同以用户为基础(User-based)的协同过滤。
- 3.产生推荐结果
以项目为基础的协同过滤不用考虑用户间的差别,所以精度比较差。但是却不需要用户的历史数据,或是进行用户识别。对于项目来讲,它们之间的相似性要稳定很多,因此可以离线完成工作量最大的相似性计算步骤,从而降低了在线计算量,提高推荐效率,尤其是在用户多于项目的情形下尤为显著。
基于项目(Item-Based)的协同过滤算法是常见的另一种算法。与 User-Based 协 同过滤算法不一样的是,Item-Based 协同过滤算法计算 Item 之间的相似度,从 而预测用户评分。也就是说该算法可以预先计算 Item 之间的相似度,这样就可 提高性能。Item-Based 协同过滤算法是通过用户评分数据和计算的 Item 相似度 矩阵,从而对目标 Item 进行预测的。
**其实与基于用户的预测方法差不多 **
2.2 算法过程
举个例子
画√表示用户购买过该物品,我们目的是要预测用户对未购买物品的兴趣度,因此就要通过公式来求
| 用户 / 物品 | 物品a | 物品b | 物品c | 物品d | 物品e |
|---|---|---|---|---|---|
| 用户 A | √ | √ | √ | ||
| 用户 B | √ | √ | |||
| 用户 C | √ | √ | |||
| 用户 D | √ | √ | √ |
2.21 建立 物品 — 用户 倒排表
物品 a:用户 A、用户 B
物品 b:用户 A、用户 C
物品 c:用户 D、用户 B
物品 d:用户 A、用户 D
物品 e:用户 C、用户 D
2.22 计算items之间的相似度
相似度计算方法
和 User-Based 协同过滤算法类似,需要先计算 Item 之间的相似度。并且计算 相似度的方法也可以采用皮尔逊关系系数或者余弦相似度,这里给出一种电子商 务系统常用的相似度计算方法,即基于物品的协同过滤算法,其中相似度计算公 式如下所示:
- 分子|N(i)∩N(j)|是同时喜欢物品 i 和 j 的用户,分母|N(i)|是喜欢物品 i 的用户数。
有了方法我们可以建立一个item-item相似度共现矩阵
| a | b | c | d | e | |
|---|---|---|---|---|---|
| a | - | 0.5 | 0.5 | 0.5 | 0 |
| b | 0.5 | - | 0 | 0.5 | 0.5 |
| c | 0.5 | 0 | - | 0.5 | 0.5 |
| d | 0.5 | 0.5 | 0.5 | - | 0.5 |
| e | 0 | 0.5 | 0.5 | 0.5 | - |
2.23 计算用户对未购买物品的兴趣度
得到物品之间的相似度后,可以根据如下公式计算用户 u 对于物品 j 的兴趣度

看不懂就看下面解释吧
其中, p ( u , j ) p(u,j) p(u,j) 表示用户 u u u 对物品 j j j 的兴趣, N ( u ) N(u) N(u) 表示用户喜欢的物品集合( i i i 是该用户喜欢的某一个物品), S ( j , k ) S(j,k) S(j,k) 表示和物品 j j j 最相似的 K K K 个物品集合, w j i w_{ji} wji 表示物品 j 和物品 i 的相似度, r u i r_{ui} rui 表示用户 u u u 对物品 i i i 的兴趣(这里简化 r u i r_{ui} rui 都等于 1,说白了就是因为原始矩阵为隐性反馈,1代表已购买)。该公式的含义是,和用户历史 上感兴趣的物品越相似的物品,越有可能在用户的推荐列表中获得比较高的排名。
- 当我们看到这里的时候很可能由于自己功底不足,很难看懂公式中的 i∈N(u)∩S(j,K)。
不过最好就是去实例中理解公式,不用记,因为大部分人没这记性
- 其中,Pa 为新用户对已有产品的向量,T 为物品相似度的共现矩阵,Pa与T做矩阵乘法得到的 P`a 为新用户对每个产品的兴趣度。
可能还是不理解这是什么,我们看是例来认识理解i∈N(u)∩S(j,K)
相似度矩阵T
| a | b | c | d | e | |
|---|---|---|---|---|---|
| a | - | 0.5 | 0.5 | 0.5 | 0 |
| b | 0.5 | - | 0 | 0.5 | 0.5 |
| c | 0.5 | 0 | - | 0.5 | 0.5 |
| d | 0.5 | 0.5 | 0.5 | - | 0.5 |
| e | 0 | 0.5 | 0.5 | 0.5 | - |
此时若有新用户 E,访问的 a,d,e 三个物品,那么可以看做向量 P:(表示如下)
那么 P`为矩阵P T相乘:

此时得到了对于用户 E,b 和 c 两个物品的兴趣度
2.24理解公式 i∈N(u)∩S(j,K)
那么现在我们来理解公式 i∈N(u)∩S(j,K): 对于用户 E,已经访问了 a,d,e,那么,N(u)={a,d,e};还有两个未访问物品 b,c, 那么 j={b,c}; 当 j=b 时,对于和物品 j 最相似的 K 个物品的集合为{a,d,e},那么 S(j,K)={a,d,e}; 得出 N(u)∩S(j,K)={a,d,e},如下图所示:
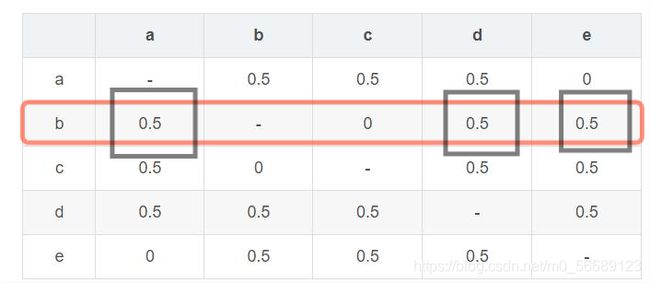

再来看矩阵相乘中的 b 行,乘以 P,实际上就是上述 N(u)∩S(j,K)={a,d,e}的相似度求和。
2.25代码实现(python)
import numpy as np
from math import sqrt
'''
用户/物品 | 物品a | 物品b | 物品c | 物品d | 物品e |
用户A | √ | √ | | √ | |
用户B | | √ | √ | | √ |
用户C | | | √ | √ | |
用户D | | √ | √ | √ | |
用户E | √ | | | √ | |
'''
#定义余弦相似性度量计算
def simil(ls_1,ls_2,n): #求item之间的相似度
fenzi=0#分子
fenmu=0#分母
n_1=n_2=0#喜欢商品的用户数初始值
for k in range(n):
#分子值为同时喜欢两个物品的用户数,若ls_1,ls_2同时为1(即用户都购买过这两件商品),相乘的1,分子加1
fenzi+=ls_1[k] * ls_2[k]
n_1 += ls_1[k]
n_2 += ls_2[k]
fenmu=sqrt(n_1*n_2)
return fenzi/fenmu#ls_1,ls_2物品相似度
#定义预测兴趣度函数
def fore(ls_1,ls_2):
return np.dot(ls_1,ls_2)
#构建用户——商品矩阵
user_item=np.array([[1,1,0,1,0],
[0,1,1,0,1],
[0,0,1,1,0],
[0,1,1,1,0],
[1,0,0,1,0]])
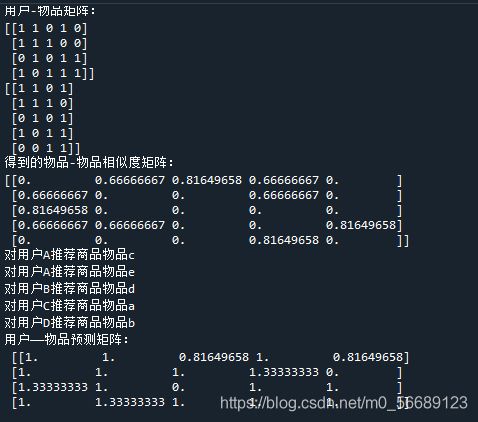
print("用户-物品矩阵:")
print(user_item)
#建立用户列表
user = ['用户A','用户B','用户C','用户D','用户E']
#建立物品列表
item = ['物品a','物品b','物品c','物品d','物品e']
n = len(user) #n个用户
m = len(item) #m个物品
#建立物品——用户倒排表
item_user=user_item.T
print("建立物品——用户倒排表:")#注意,倒排表其实就是将矩阵item_user倒置
print(item_user)
#建立物品——物品相似度共现矩阵
sim = np.zeros((m,m)) #相似度矩阵,默认全为0
#下面对相似度空矩阵循环并填充
for i in range(m):
for j in range(m):
if i < j:
sim[i][j] = simil(item_user[i],item_user[j],n)
sim[j][i] = sim[i][j]
#为了更好地拟合用户对商品的的兴趣度,我们引入最相似的K件商品
#在这里我改变了一种思想,我将相似度大于0.5的两间商品定义为最相似的物品行列
#下面修改相似度矩阵,剔除相似度小于0.5的数据,目的是为了之后求取兴趣度时预测更精准
for i in range(m):
for j in range(m):
if sim[i][j]<0.5:
sim[i][j]=0
print("得到的物品-物品相似度矩阵:")
print(sim) #打印物品-物品相似度矩阵
#相似度矩阵有了,我们预测兴趣度
REuser_item=np.array([[1.,1.,0.,1.,0.],
[0.,1.,1.,0.,1.],
[0.,0.,1.,1.,0.],
[0.,1.,1.,1.,0.],
[1.,0.,0.,1.,0.]])#复制一个原矩阵
for i in range(n):#遍历用户
for j in range(m):#遍历商品
if user_item[i][j]==0:#将原矩阵里空兴趣度进行预测并填补到预测空矩阵中
REuser_item[i][j]=fore(sim[j],user_item[i])
if REuser_item[i][j]>0.8:
print("对{:}推荐商品{:}".format(user[i],item[j]))
print("用户——物品预测矩阵:\n",REuser_item)