opencv入门：傅里叶变换

傅里叶变换

图像处理一般分为空间域处理和频率域处理。空间域处理直接对图像内的像素进行处理，空间域处理主要划分为灰度变换和空间滤波两种形式。灰度变换时对图像内单个像素值进行处理，比如调节对比度和处理阈值。空间滤波设计图像质量的改变，比如平滑处理。空间域处理的计算简单方便，运行速度更快。

频率预处理是先将图像变换到频率域，然后再频率域对图像进行处理，最后再通过反变换将图像从频率域转换到空间域。傅里叶变换是应用最广的一种频域转换，可以将图像从空间域变换到频率域，逆傅里叶变换可以将频率域的信息变换到空间域内。傅里叶变换再图像处理领域内又非常重要的作用。。。傅里叶学过但是忘了。。

找到了两篇非常不错的文章，将傅里叶变换原理啊，作用啊什么的脑补链接（个人更喜欢这个），脑补链接

这个图总结的是真的好。。。

理论基础

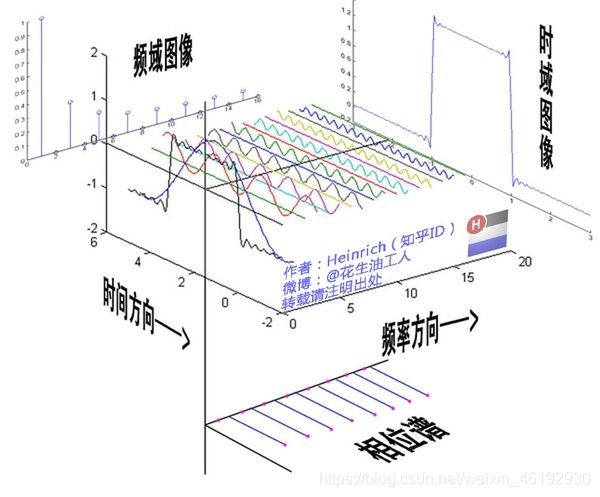
傅里叶变换非常抽象，傅里叶指出，任何周期函数都可以表示为不同频率的正选函数和的形式。

从频域角度考虑，上述三个正弦函数可以分别表示为三个柱子。横坐标是频率，纵坐标是振幅。

由14-5左上 时域函数图像，构造出14-6的频域图像的过程就是傅里叶变换。。傅里叶变换就是从频域的角度完整地表述时域信息。

这样增加个时间差，傅里叶变换中就是相位。相位不同构成的图像也不同。

图像处理中，傅里叶变换就是将图像分解为正弦分量和余弦分量两部分。将图像从空间域转换到频域。数字图像经过傅里叶变换后得到的频域值是复数。因此，显示傅里叶变换的结果需要使用 实数图像 加 虚数图像，或者 幅度图像 加 相位图像的形式。

幅度图像保留原图中我们需要的大部分信息，再图像处理中，通常仅使用幅度图像，如果希望再领域内对图像进行处理，再通过逆傅里叶变换得到修改后的空域图像，还是要保留幅度图和相位图。

对图像进行傅里叶变换后，会得到图像中的低频号高频信息，低频信息对应图像内变换缓慢的灰度分量，高频信息对应图像内变换越来越快的灰度分量，是由灰度的尖锐过度造成的。例如，在一幅大草原的图像中有一头狮子，低频信息就对应着广袤的颜色趋于一致的草原等细节信息，而高频信息则对应着狮子的轮廓等各种边缘及噪声信息。

傅里叶变换的目的，就是为了将图像从空域转换到频域，并在频域内实现对图像内特定对象的处理，然后再对经过处理的频域图像进行逆傅里叶变换得到空域图像。傅里叶变换在图像处理领域发挥着非常关键的作用，可以实现图像增强、图像去噪、边缘检测、特征提取、图像压缩和加密等。

Numpy实现傅里叶变换

实现傅里叶变换

返回值 = numpy.fft.fft2(原始图像) 参数是灰度图，返回值是一个复数数组。经过该函数的处理，会得到图像的频谱信息，此时，图像频谱中的零频率分量位于频谱图像（频域图像）的左上角，通常使用 numpy.fft.fftshift() 来将零频率成分移动到频域图像的中心位置。返回值=numpy.fft.fftshift(原始频谱) 这对于观察傅里叶变换后频谱中的零频率部分非常有效。为了便于频域的滤波和频谱的分析，常常在变换之前进行频谱的中心化。

我们得到的是一个复数数组，为了显示图像，需要将他们的值调到 [0,255] 的灰度空间中。像素新值=20*np.log(np.abs(频谱值))

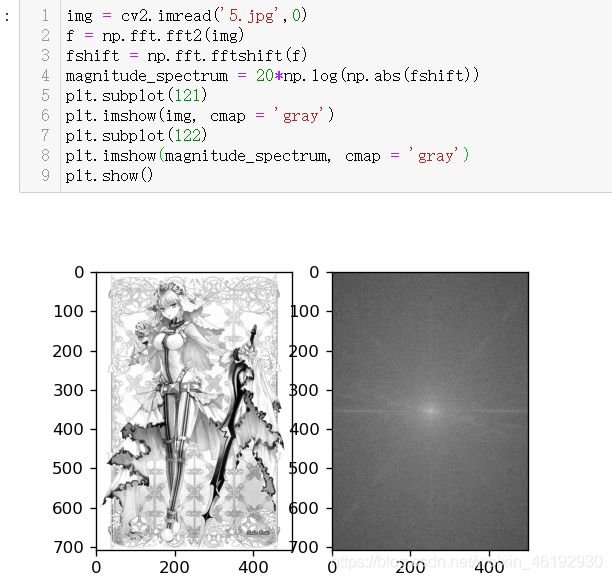
得到了频谱图。。。反正我是看不懂这频谱图到底是啥，，脑补链接，，数学是真的真的真的太厉害了。。。

实现逆傅里叶变换

需要先使用 numpy.fft.ifftshift()函数将零频率分量移到原来的位置，再进行逆傅里叶变换 返回值=numpy.fft.ifft2(频域数据) 实现逆傅里叶变换，返回值仍然是一个复数数组。iimg = np.abs(逆傅里叶变换结果) 将信息调整到 [0,255] 的灰度空间内。

img = cv2.imread('5.jpg',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'),plt.axis('off')
plt.show()        # 得到的图像是一样的。

高通滤波示例

一副图像内，存在高频信号和低频信号。滤波器可以允许一定频率的分量通过或者拒绝其通过，按照其作用方式分为，低通滤波器和高通滤波器。低通滤波器使高频信号衰减而对低频信号放行，会使图像变模糊。高通滤波器使低频信号衰减而让高频信号通过，将增强图像中尖锐的细节，但是会导致图像的对比度降低。

傅里叶变换可以将图像的高频信号和低频信号分离，例如，将低频信号放到傅里叶变化图像的中心位置。经过处理低频信号位于频谱图像的中心位置，从而进行分别处理。例如 高通滤波或者低通滤波再对图像的高频或低频信号进行处理后，再返回空域，就完成了对图像的频域处理。频域处理可以实现图像增强，图像去噪，边缘检测，特征提取，压缩和加密等操作。

右图通过高通滤波将图像中的低频分量值替换为0，屏蔽了低频信号，只保留高频信号，实现高通滤波。

保留图像的边缘信息，，，额是不是就是保留细节啊。。

OpenCV实现傅里叶变换

实现傅里叶变换

返回结果=cv2.dft(原始图像，转换标识)

• 原始图像，首先要使用 np.float32()函数将图像转换为 np.float32格式
• 转换标识的值通常为 cv2.DFT_COMPLEX_OUTPUT 用来输出一个复数阵列。

cv2.dft() 返回结果域 Numpy 进行傅里叶变换得到的结果是一致的，但是返回的是双通道，第一个是结果的实数部分，第二个是虚数部分。但是还是需要 np.fft.fftshift() 将零频率分量转移到中心位置。

经过处理频谱图像还是由一个实部和虚部构成的值，要想显示还是要处理。

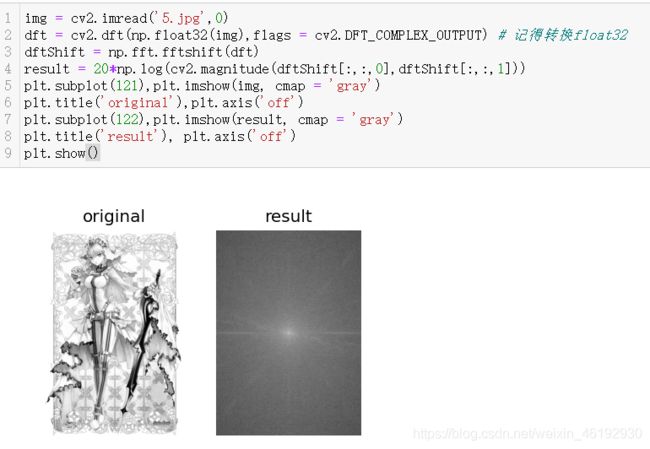
返回值 = cv2.magnitude( 参数1，参数2) 计算频谱信息的幅度，参数1，浮点型x坐标的值，也就是实部，参数2 就是虚部了，必须和参数1具有相同的大小（size 值大小，不是value值的大小），函数返回值是参数1 和参数2 的平方根。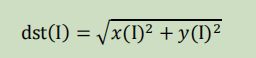
I 是原图，dst 目标图像。result = 20*np.log(cv2.magnitude(实部,虚部)) 得到频谱信息的幅度后，还要对幅度值进行进一步转换，到灰度空间的值范围，以显示图像。

实现逆傅里叶变换

返回结果=cv2.idft(原始数据) 逆傅里叶变换后，通常会将零频率分量移至频谱图像的中心位置，如果使用 fftshift() 移动了零频率分量，再逆傅里叶变换前 使用 ifftshift 将零频率分量恢复到原来位置。还有逆傅里叶后结果仍是复数，使用cv2.magnitude() 计算幅度。

img = cv2.imread('5.jpg',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
ishift = np.fft.ifftshift(dftShift)
iImg = cv2.idft(ishift)
iImg= cv2.magnitude(iImg[:,:,0],iImg[:,:,1])

低通滤波示例

将傅里叶变换结果图像中的高频信号值替换为0，屏蔽高频信号，保留低频信号，实现低通道滤波。

削弱了边缘信息，变得很模糊。