认知无线电----能量检测法原理介绍及MATLAB实现
认知无线电
随着无线通信的快速发展,用户对通信质量的要求越来越高,同时无线设备的大幅度增长,使得频谱资源显得更加重要。认知无线电(Cognitive Radio, CR)技术被当作解决频谱资源紧张、提高频谱利用率的强有力的技术,是下一代通信技术的重要组成成分。频谱感知是认知无线电技术实现的关键技术,通过频谱感知技术来感知信道中的频谱空洞,使得认知用户可以利用频谱空洞进行信息的传输,从而缓解了频谱资源紧张与通信业务需求之间的矛盾。
这里简单介绍频谱感知的比较经典的一种方法——能量检测方法(Energy Detection,ED)。
能量检测方法原理介绍
信号的检测问题可以看作是二元假设问题
x ( t ) = { n ( t ) , H 0 s ( t ) + n ( t ) , H 1 x\left( t \right)=\left\{ \begin{aligned} & n\left( t \right)\ \ \ \ \ \ \ \ \ ,\ \ \ \ \ {{H}_{0}} \\ & s\left( t \right)+n\left( t \right),\ \ \ \ {{H}_{1}} \\ \end{aligned} \right. x(t)={n(t) , H0s(t)+n(t), H1
其中, s ( t ) s\left( t \right) s(t)表示信号, n ( t ) n\left( t \right) n(t)表示噪声,其方差可以设为 σ 2 {{\sigma }^{2}} σ2, H i {{H}_{i}} Hi, i = 0 , 1 i=0,1 i=0,1表示不同假设。
在观测时间 T T T中,计算接收信号的能量与门限 t h th th进行比较,如果大于门限 t h th th的话,则判为 H 1 {{H}_{1}} H1,即有信号;否则判为 H 0 {{H}_{0}} H0,即无信号。
在实际中一般采用的数字信号,那么接收信号可以表示为
x ( i ) = { n ( i ) , H 0 s ( i ) + n ( i ) , H 1 , i = 1 , 2 , ⋯ , N x\left( i \right)=\left\{ \begin{aligned} & n\left( i \right)\ \ \ \ \ \ \ \ \ ,\ \ \ \ \ {{H}_{0}} \\ & s\left( i \right)+n\left( i \right),\ \ \ \ \ {{H}_{1}} \\ \end{aligned} \right.,\ \ \ \ \ i=1,2,\cdots ,N x(i)={n(i) , H0s(i)+n(i), H1, i=1,2,⋯,N
其中, N N N表示的是样本点数。那么检验统计量 D D D可以表示为
D = ∑ i x 2 ( i ) D=\sum\limits_{i}^{{}}{{{x}^{2}}\left( i \right)} D=i∑x2(i)
可以证明,该检验统计量近似服从高斯分布,具体为
H 0 : D ~ N o r m a l ( N σ 2 , 2 N σ 4 ) H 1 : D ~ N o r m a l ( N ( σ 2 + σ s 2 ) , 2 N ( σ 2 + σ s 2 ) 2 ) \begin{aligned} & {{H}_{0}}:D\tilde{\ }Normal\left( N{{\sigma }^{2}},2N{{\sigma }^{4}} \right) \\ & {{H}_{1}}:D\tilde{\ }Normal\left( N\left( {{\sigma }^{2}}+\sigma _{s}^{2} \right),2N{{\left( {{\sigma }^{2}}+\sigma _{s}^{2} \right)}^{2}} \right) \\ \end{aligned} H0:D ~Normal(Nσ2,2Nσ4)H1:D ~Normal(N(σ2+σs2),2N(σ2+σs2)2)
其中, σ s 2 \sigma _{s}^{2} σs2表示信号的平均功率。
对于恒虚警检测来说,当信号不存在的时候可以通过虚警概率 P f {{P}_{f}} Pf来确定检测门限 t h th th,这是由于在 H 0 {{H}_{0}} H0的假设条件下,检验统计量 D D D服从高斯分布,虚警概率
P f = P ( D > t h ∣ H 0 ) {{P}_{f}}=P\left( D>th|{{H}_{0}} \right) Pf=P(D>th∣H0)
那么可以得到
P f = Q ( t h − N σ 2 2 N σ 4 ) {{P}_{f}}=Q\left( \frac{th-N{{\sigma }^{2}}}{\sqrt{2N{{\sigma }^{4}}}} \right) Pf=Q(2Nσ4th−Nσ2)
其中, Q ( x ) = 1 2 π ∫ x + ∞ e − t 2 / 2 d t Q\left( x \right)=\frac{1}{\sqrt{2\pi }}\int_{x}^{+\infty }{{{e}^{-{{t}^{2}}/2}}dt} Q(x)=2π1∫x+∞e−t2/2dt
那么检测门限 t h th th可以通过上式进行计算
t h = σ 2 ( N + 2 N Q − 1 ( P f ) ) th={{\sigma }^{2}}\left( N+\sqrt{2N}{{Q}^{-1}}\left( {{P}_{f}} \right) \right) th=σ2(N+2NQ−1(Pf))
同样,在 H 1 {{H}_{1}} H1的假设条件下,可以利用归一化的方法得到,检验统计量 D D D也服从高斯分布,那么检测概率可以表示为
P d = P ( D > t h ∣ H 1 ) = Q ( t h − N ( σ 2 + σ s 2 ) 2 N ( σ 2 + σ s 2 ) 2 ) {{P}_{d}}=P\left( D>th|{{H}_{1}} \right)=Q\left( \frac{th-N\left( {{\sigma }^{2}}+\sigma _{s}^{2} \right)}{\sqrt{2N{{\left( {{\sigma }^{2}}+\sigma _{s}^{2} \right)}^{2}}}} \right) Pd=P(D>th∣H1)=Q⎝⎛2N(σ2+σs2)2th−N(σ2+σs2)⎠⎞
将门限 t h th th带入,可以求的系统的检测概率。
当然能量也可以使用归一化的能量进行判决。此外,还有采用多个门限进行判决,提高检测概率,这里就不再叙述。
下面根据恒虚警检测的原理,通过仿真虚警概率 P f {{P}_{f}} Pf和检测概率 P d {{P}_{d}} Pd之间的关系.
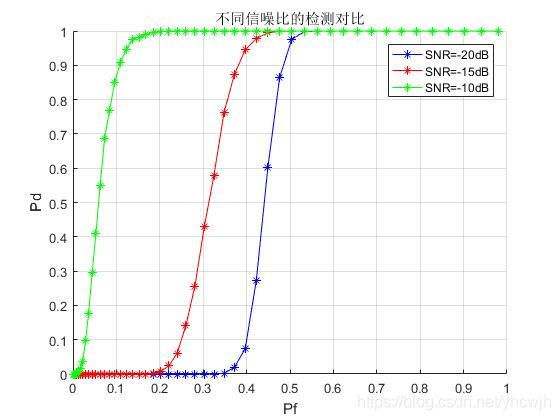
从图中可以看出,随着信噪比的增加,相同虚警概率的条件下,检测概率越大,这也是和实际相符合的,即信道条件越好越容易检测出信号。
代码如下:
clear;
close all;
clc;
T = 50;
Fs = 100;
N =Fs*T; %采样点数
Mc = 1000; %蒙特卡洛实验次数
Pf =(0.01:0.02:1).^2; %虚警概率
SNR_db(1) = -25;
SNR_db(2) = -20;
SNR_db(3) = -15;
for i = 1:3
SNR(i) = power(10,SNR_db(i)/10);
end
for i=1:length(Pf)
for m=1:3
s_awgn = 0;
for kk = 1:Mc
t = ((kk-1)*N+1:kk*N)/Fs; %时间轴
x = randi([0 1],1,100)*2-1;
xx = rectpulse(x,N/100);
x = xx.*sin(2*pi*10*t);
ps = sum(abs(x).^2)/length(x);
noise = randn(1,N);
noise = noise-mean(noise);
noise_awgn = sqrt(ps/SNR(m))*noise/std(noise);
%高斯信道
re_sig = x + noise_awgn; %接收信号
th(i) = ps/SNR(m)*(N+sqrt(2*N)*sqrt(2)*erfcinv(2*Pf(i))); %门限值
power(i) = sum(re_sig.^2); %接收信号能量
if power(i) > th(i)
s_awgn = s_awgn + 1; %进行判决
end
end
Pd_sim_awgn(m,i) = s_awgn/Mc; %仿真高斯检测概率
end
end
figure
hold on;
plot(Pf,Pd_sim_awgn(1,:),'*-b',Pf,Pd_sim_awgn(2,:),'*-r',Pf,Pd_sim_awgn(3,:),'*-g');
grid on
legend('SNR=-20dB','SNR=-15dB', 'SNR=-10dB');
title ('不同信噪比的检测对比')
xlabel('Pf');
ylabel('Pd');
参考文献
[1]H. Urkowitz, “Energy detection of unknown deterministic signals,” in Proceedings of the IEEE, vol. 55, no. 4, pp. 523-531, April 1967, doi: 10.1109/PROC.1967.5573.
[2]潘建国,翟旭平.基于能量检测的频谱感知方法[J].上海大学学报(自然科学版),2009,15(01):54-59.