C语言----实现 Trie (前缀树或字典树)

        用了这么多年的命令补齐，之前也没想过命令补齐是怎么去实现的，正好该题有机会去了解这种数据结构，字典树。

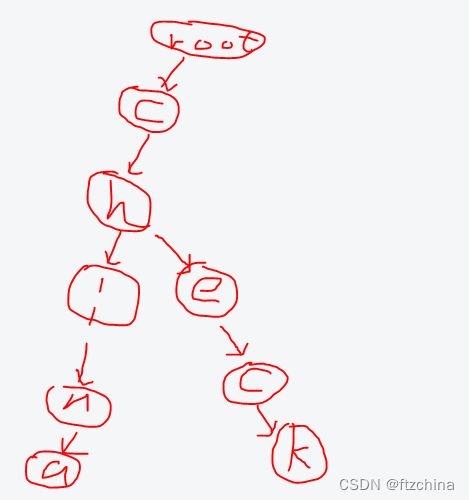
        对于插入一个单词，就是从字典树的根节点每个字母依次按照树形结构插入直到单词结束，比如我要插入两个单词，china和check，其结构如下

插入字符串

        我们从字典树的根开始，插入字符串。对于当前字符对应的子节点，有两种情况：

1，子节点存在。沿着指针移动到子节点，继续处理下一个字符。

2，子节点不存在。创建一个新的子节点，记录在 child 数组的对应位置上，然后沿着指针移动到子节点，继续搜索下一个字符。
重复以上步骤，直到处理字符串的最后一个字符，然后将当前节点标记为字符串的结尾。

查找前缀

我们从字典树的根开始，查找前缀。对于当前字符对应的子节点，有两种情况：

1，子节点存在。沿着指针移动到子节点，继续搜索下一个字符。
2，子节点不存在。说明字典树中不包含该前缀，返回空指针。
重复以上步骤，直到返回空指针或搜索完前缀的最后一个字符。

若搜索到了前缀的末尾，就说明字典树中存在该前缀。此外，若前缀末尾对应节点的 ,isEnd 为真，则说明字典树中存在该字符串。

typedef struct trie
{
    struct trie *child[26];
    bool isEnd;
} Trie;


Trie* trieCreate() 
{
    Trie *newNode = (Trie*)malloc(sizeof(Trie));
    memset(newNode->child,0,sizeof(newNode->child));
    newNode -> isEnd = false;

    return newNode;
}
 
void trieInsert(Trie* obj, char * word) 
{
    for(int i=0; ichild[index] == NULL)
        {
            obj->child[index] = trieCreate();
        }
        obj = obj->child[index];
    }
    obj->isEnd = true;
}

bool trieSearch(Trie* obj, char * word) 
{
    for(int i=0; ichild[index] == NULL)
            return false;
        obj = obj->child[index];
    }
    return obj->isEnd;
}

bool trieStartsWith(Trie* obj, char * prefix) 
{
    for(int i=0; ichild[index] == NULL)
            return false;
        obj = obj->child[index];
    }
    return true;
}

void trieFree(Trie* obj) 
{
    for(int i=0; i<26; i++)
    {
        if(obj->child[i] != NULL)
            trieFree(obj->child[i]);
    }
    free(obj);
}

/**
 * Your Trie struct will be instantiated and called as such:
 * Trie* obj = trieCreate();
 * trieInsert(obj, word);
 
 * bool param_2 = trieSearch(obj, word);
 
 * bool param_3 = trieStartsWith(obj, prefix);
 
 * trieFree(obj);
*/

运行结果