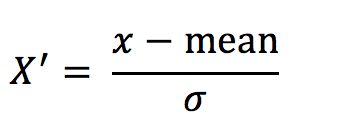1. 机器学习概述与特征工程

1.机器学习概述

1.机器学习工作流程

学习目标

• 了解机器学习的定义
• 知道机器学习的工作流程
• 掌握获取到的数据集的特性

---

1 什么是机器学习

机器学习是从数据中自动分析获得模型，并利用模型对未知数据进行预测。

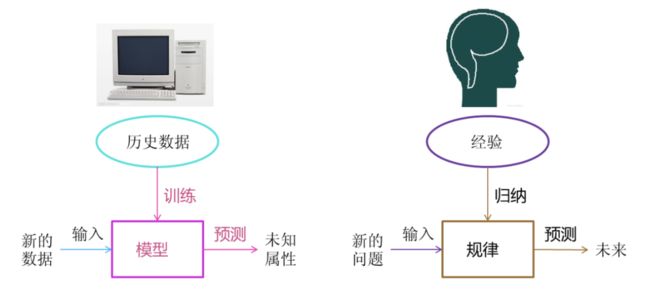
2 机器学习工作流程

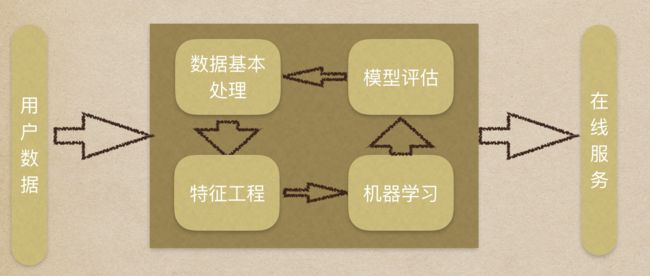
2.1 获取到的数据集介绍

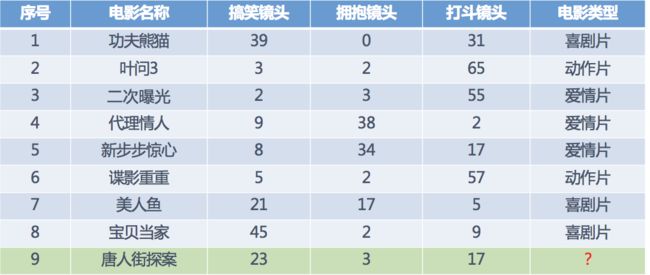
• 数据简介

  在数据集中一般：

  • 一行数据我们称为一个样本
  • 一列数据我们成为一个特征
  • 有些数据有目标值（标签值），有些数据没有目标值（如上表中，电影类型就是这个数据集的目标值）

• 数据类型构成：

  • 数据类型一：特征值+目标值（目标值是连续的和离散的）
  • 数据类型二：只有特征值，没有目标值

• 数据分割：

  • 机器学习一般的数据集会划分为两个部分：
    • 训练数据：用于训练，构建模型
    • 测试数据：在模型检验时使用，用于评估模型是否有效
  • 划分比例：
    • 训练集：70% 80% 75%
    • 测试集：30% 20% 25%

2.2 数据基本处理

即对数据进行缺失值、去除异常值等处理

2.3 特征工程

2.3.1什么是特征工程

特征工程是使用专业背景知识和技巧处理数据，使得特征能在机器学习算法上发挥更好的作用的过程。

• 意义：会直接影响机器学习的效果

2.3.2 为什么需要特征工程(Feature Engineering)

机器学习领域的大神Andrew Ng(吴恩达)老师说“Coming up with features is difficult, time-consuming, requires expert knowledge. “Applied machine learning” is basically feature engineering. ”

注：业界广泛流传：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。

2.3.3 特征工程包含内容

• 特征提取
• 特征预处理
• 特征降维

2.3.4 各概念具体解释

• 特征提取

  • 将任意数据（如文本或图像）转换为可用于机器学习的数字特征

• 特征预处理

  • 通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程

• 特征降维

  • 指在某些限定条件下，降低随机变量(特征)个数，得到一组“不相关”主变量的过程

    

2.4 机器学习

选择合适的算法对模型进行训练

2.5 模型评估

对训练好的模型进行评估

3 小结

• 机器学习定义【掌握】
  • 机器学习是从数据中自动分析获得模型，并利用模型对未知数据进行预测
• 机器学习工作流程总结【掌握】
  • 1.获取数据
  • 2.数据基本处理
  • 3.特征工程
  • 4.机器学习(模型训练)
  • 5.模型评估
    • 结果达到要求，上线服务
    • 没有达到要求，重新上面步骤
• 获取到的数据集介绍【掌握】
  • 数据集中一行数据一般称为一个样本，一列数据一般称为一个特征。
  • 数据集的构成：
    • 由特征值+目标值（部分数据集没有）构成
  • 为了模型的训练和测试，把数据集分为：
    • 训练数据（70%-80%）和测试数据（20%-30%）
• 特征工程包含内容【了解】
  • 特征提取
  • 特征预处理
  • 特征降维

2 机器学习算法分类

学习目标

• 了解机器学习常用算法的分类

---

根据数据集组成不同，可以把机器学习算法分为：

• 监督学习
• 无监督学习
• 半监督学习
• 强化学习

1 监督学习

• 定义：
  • 输入数据是由输入特征值和目标值所组成。
    • 函数的输出可以是一个连续的值(称为回归），
    • 或是输出是有限个离散值（称作分类）。

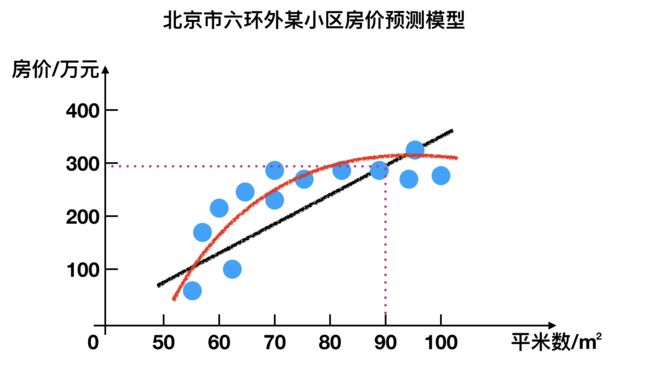
1.1 回归问题

例如：预测房价，根据样本集拟合出一条连续曲线。

1.2 分类问题

例如：根据肿瘤特征判断良性还是恶性，得到的是结果是“良性”或者“恶性”，是离散的。

2 无监督学习

• 定义：

  • 输入数据是由输入特征值组成，没有目标值
    • 输入数据没有被标记，也没有确定的结果。样本数据类别未知；
    • 需要根据样本间的相似性对样本集进行类别划分。

  举例：

有监督，无监督算法对比：

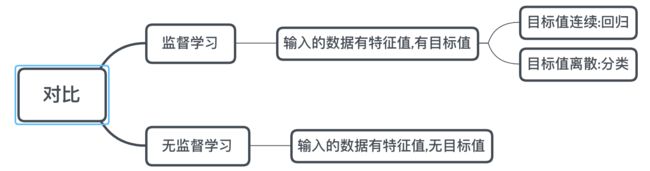
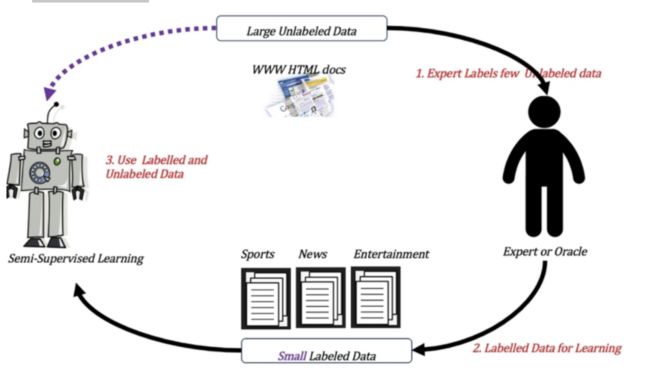
3 半监督学习

• 定义：
  • 训练集同时包含有标记样本数据和未标记样本数据。

举例：

• 监督学习训练方式：

• 半监督学习训练方式

  

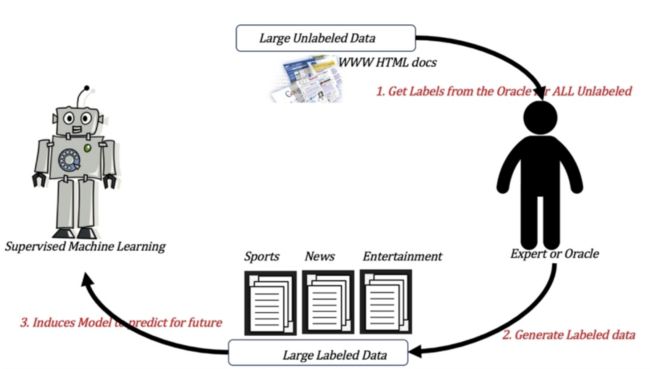
4 强化学习

• 定义：
  • 实质是make decisions 问题，即自动进行决策，并且可以做连续决策。

举例：

小孩想要走路，但在这之前，他需要先站起来，站起来之后还要保持平衡，接下来还要先迈出一条腿，是左腿还是右腿，迈出一步后还要迈出下一步。

小孩就是 agent，他试图通过采取行动（即行走）来操纵环境（行走的表面），并且从一个状态转变到另一个状态（即他走的每一步），当他完成任务的子任务（即走了几步）时，孩子得到奖励（给巧克力吃），并且当他不能走路时，就不会给巧克力。

主要包含五个元素：agent, action, reward, environment, observation；

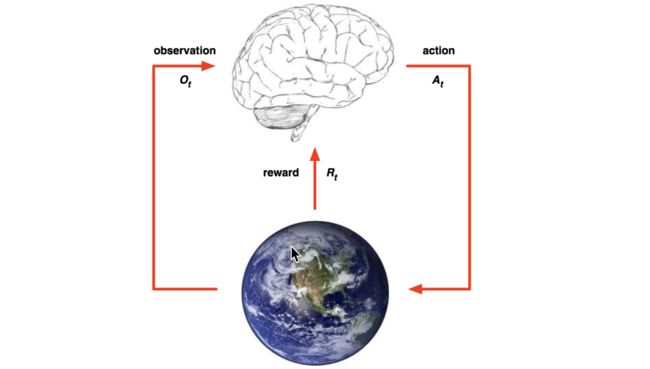
强化学习的目标就是获得最多的累计奖励。

监督学习和强化学习的对比

	监督学习	强化学习
反馈映射	输出的是之间的关系，可以告诉算法什么样的输入对应着什么样的输出。	输出的是给机器的反馈 reward function，即用来判断这个行为是好是坏。
反馈时间	做了比较坏的选择会立刻反馈给算法。	结果反馈有延时，有时候可能需要走了很多步以后才知道以前的某一步的选择是好还是坏。
输入特征	输入是独立同分布的。	面对的输入总是在变化，每当算法做出一个行为，它影响下一次决策的输入。

拓展阅读：Alphago进化史 漫画告诉你Zero为什么这么牛：

http://sports.sina.com.cn/chess/weiqi/2017-10-21/doc-ifymyyxw4023875.shtml

5 小结

	In	Out	目的	案例
监督学习 (supervised learning)	有标签	有反馈	预测结果	猫狗分类 房价预测
无监督学习 (unsupervised learning)	无标签	无反馈	发现潜在结构	“物以类聚，人以群分”
半监督学习 (Semi-Supervised Learning)	部分有标签，部分无标签	有反馈	降低数据标记的难度
强化学习 (reinforcement learning)	决策流程及激励系统	一系列行动	长期利益最大化	学下棋

• 监督学习(supervised learning)（预测）
  • 定义：输入数据是由输入特征值和目标值所组成。函数的输出可以是一个连续的值(称为回归），或是输出是有限个离散值（称作分类）。
  • 分类 k-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归、神经网络
  • 回归 线性回归、岭回归
• 无监督学习(unsupervised learning)
  • 定义：输入数据是由输入特征值所组成。
  • 聚类 k-means

2.特征工程

1 数据集

1.1 scikit-learn数据集API介绍

目标

• 知道sklearn中获取数据集的方法
• 知道sklearn中对数据集的划分方法

API介绍

• sklearn.datasets
  • 加载获取流行数据集
  • datasets.load_*()
    • 获取小规模数据集，数据包含在datasets里
  • datasets.fetch_*(data_home=None)
    • 获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录,默认是 ~/scikit_learn_data/

sklearn小数据集

• sklearn.datasets.load_iris()

  加载并返回鸢尾花数据集

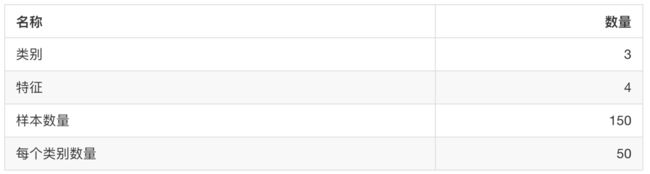
sklearn大数据集

• sklearn.datasets.fetch_20newsgroups(data_home=None,subset=‘train’)
  • subset：‘train’或者’test’，‘all’，可选，选择要加载的数据集。
  • 训练集的“训练”，测试集的“测试”，两者的“全部”

1.2 sklearn数据集返回值介绍

• load和fetch返回的数据类型datasets.base.Bunch(字典格式)
  • data：特征数据数组，是 [n_samples * n_features] 的二维 numpy.ndarray 数组
  • target：标签数组，是 n_samples 的一维 numpy.ndarray 数组
  • DESCR：数据描述
  • feature_names：特征名,新闻数据，手写数字、回归数据集没有
  • target_names：标签名

from sklearn.datasets import load_iris
# 获取鸢尾花数据集
iris = load_iris()
print("鸢尾花数据集的返回值：\n", iris)
# 返回值是一个继承自字典的Bench
print("鸢尾花的特征值:\n", iris["data"])
print("鸢尾花的目标值：\n", iris.target)
print("鸢尾花特征的名字：\n", iris.feature_names)
print("鸢尾花目标值的名字：\n", iris.target_names)
print("鸢尾花的描述：\n", iris.DESCR)

1.3 数据集的划分

机器学习一般的数据集会划分为两个部分：

• 训练数据：用于训练，构建模型
• 测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

• 训练集：70% 80% 75%
• 测试集：30% 20% 25%

数据集划分api

• sklearn.model_selection.train_test_split(arrays, *options)
  • 参数：
    • x 数据集的特征值
    • y 数据集的标签值
    • test_size 测试集的大小，一般为float
    • random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
  • return
    • x_train, x_test, y_train, y_test

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 1、获取鸢尾花数据集
iris = load_iris()
# 对鸢尾花数据集进行分割
# 训练集的特征值x_train 测试集的特征值x_test 训练集的目标值y_train 测试集的目标值y_test
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
print("x_train:\n", x_train.shape)
# 随机数种子
x_train1, x_test1, y_train1, y_test1 = train_test_split(iris.data, iris.target, random_state=6)
x_train2, x_test2, y_train2, y_test2 = train_test_split(iris.data, iris.target, random_state=6)
print("如果随机数种子不一致：\n", x_train == x_train1)
print("如果随机数种子一致：\n", x_train1 == x_train2)

1.4 总结

• 获取数据集【知道】
  • 小数据:
    • sklearn.datasets.load_*
  • 大数据集:
    • sklearn.datasets.fetch_*
• 数据集返回值介绍【知道】
  • 返回值类型是bunch–是一个字典类型
  • 返回值的属性:
    • data：特征数据数组
    • target：标签(目标)数组
    • DESCR：数据描述
    • feature_names：特征名,
    • target_names：标签(目标值)名
• 数据集的划分【掌握】
  • sklearn.model_selection.train_test_split(arrays, *options)
  • 参数:
    • x – 特征值
    • y – 目标值
    • test_size – 测试集大小
    • ramdom_state – 随机数种子
  • 返回值:
    • x_train, x_test, y_train, y_test

2.特征抽取

2.1 字典特征抽取

# DictVectorizer（）
from sklearn.feature_extraction import DictVectorizer
def dict_demo():
    '''
    字典特征抽取
        1.实例化sklearn功能函数
        2.调用fit_transform（数据的根据实例化函数的功能，对数据进行响应的处理。）
        3.print
    :return:
    '''
    data = [{'city': '北京', 'temperature': 100}, {'city': '上海', 'temperature': 60}, {'city': '深圳', 'temperature': 30}]
    print(data)
    # 1.实例化一个转换器类
    # sparse默认False 则返回稀疏矩阵，将非零值 按位置表示出来。可以节省内存
    transfer = DictVectorizer(sparse=False)
    # 2.调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("data_new\n", data_new)
    print("特征名字：\n", transfer.get_feature_names_out())
    return None
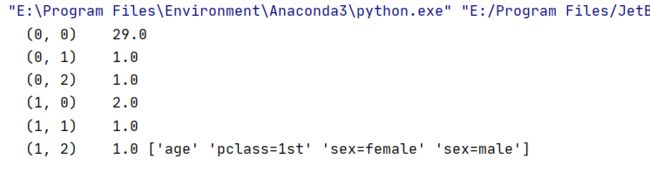
def dect_demo2():
     transfer = DictVectorizer()
    # 2.调用fit_transform()
    data = [{'pclass': '1st', 'age': 29.0, 'sex': 'female'},
            {'pclass': '1st', 'age': 2.0, 'sex': 'female'},
            {'pclass': '1st', 'age': 30.0, 'sex': 'male'},
            {'pclass': '1st', 'age': 25.0, 'sex': 'female'},
            {'pclass': '1st', 'age': 0.9167, 'sex': 'male'},
            {'pclass': '1st', 'age': 47.0, 'sex': 'male'},
            {'pclass': '1st', 'age': 63.0, 'sex': 'female'},
            {'pclass': '1st', 'age': 39.0, 'sex': 'male'},
            {'pclass': '1st', 'age': 58.0, 'sex': 'female'},
            {'pclass': '1st', 'age': 71.0, 'sex': 'male'}]
    data_new = transfer.fit_transform(data)
    print(data_new[:2], transfer.get_feature_names_out())

2.2 英文文本特征抽取

# CountVectorizer（） 统计出现次数
from sklearn.feature_extraction.text import CountVectorizer
def count_english_demo():
    '''
    文本特征抽取：CountVecotrizer()  统计每个样本文字出现的个数
    :return:
    '''
    data = ["life is short,i like like python", "life is too long,i dislike python"]
    # 1.实例化一个转换器类 stop_words停用词
    transfer = CountVectorizer(stop_words=["is", "too"])
    # 2.调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new.toarray())
    print("特征名字：\n", transfer.get_feature_names_out())
    return None

2.3 中文分词

def cut_word(text):
    '''
    进行中文分词：“我爱北京天安门”-->“我 爱 北京 天安门”
    :param text:
    :return:
    '''
    return " ".join(list(jieba.cut(text)))

2.4中文文本特征抽取

from sklearn.feature_extraction.text import CountVectorizer
def count_chinese_demo1():
    '''
      文本特征抽取：CountVecotrizer()  统计每个样本文字出现的个数
      :return:
      '''
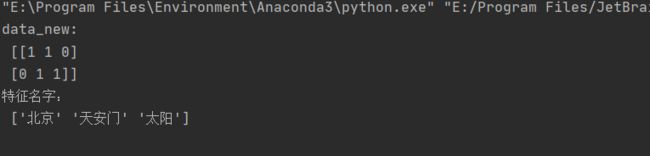
    data = ["我 爱 北京 天安门", "天安门 上 太阳 升"]
    # 1.实例化一个转换器类
    transfer = CountVectorizer()
    # 2.调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new.toarray())
    print("特征名字：\n", transfer.get_feature_names_out())
    return None

import jieba
from sklearn.feature_extraction.text import CountVectorizer
def cut_word(text):
    '''
    进行中文分词：“我爱北京天安门”-->“我 爱 北京 天安门”
    :param text:
    :return:
    '''
    return " ".join(list(jieba.cut(text)))


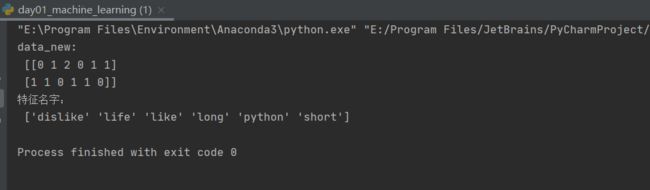
def count_chinese_demo2():
    '''
      文本特征抽取：CountVecotrizer()  统计每个样本文字出现的个数
      :return:
      '''
    # 1.将中文文本进行分词
    data = ["一种还是一种今天很残酷，明天更残酷，后天很美好，但绝对大部分是死在明天晚上，所以每个人不要放弃今天。",
            "我们看到的从很远星系来的光是在几百万年之前发出的，这样当我们看到宇宙时，我们是在看它的过去。",
            "如果只用一种方式了解某样事物，你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
    data_new = []
    for sentence in data:
        data_new.append(cut_word(sentence))
    print("分词后的新数据\n",data_new)
    # 2.实例化一个转换器类
    transfer = CountVectorizer(stop_words=["一种"])
    # 3.调用fit_transform
    data_final = transfer.fit_transform(data_new)
    print("data_final:\n", data_final.toarray())
    print("特征名字：\n", transfer.get_feature_names_out())
    return None

2.5根据重要性对文本特征抽取

TF-IDF - 重要程度
两个词 “经济”，“非常”
1000篇文章-语料库
100篇文章 - "非常"
10篇文章 - “经济”
两篇文章
文章A(100词) : 10次“经济” TF-IDF:0.2
    tf:10/100 = 0.1
    idf:lg 1000/10 = 2
文章B(100词) : 10次“非常” TF-IDF:0.1
    tf:10/100 = 0.1
    idf: log 10 1000/100 = 1
    对数？
        2 ^ 3 = 8
        log 2 8 = 3
        log 10 10 = 1
TF - 词频（term frequency，tf)
IDF - 逆向文档频率

# TfidfVectorizer 根据重要性程度进行抽取
from sklearn.feature_extraction.text import TfidfVectorizer
def tdidf_demo():
    '''
    用TF-IDF的方法进行文本特征抽取
    :return:
    '''
    # 1.将中文文本进行分词
    data = ["一种还是一种今天很残酷，明天更残酷，后天很美好，但绝对大部分是死在明天晚上，所以每个人不要放弃今天。",
            "我们看到的从很远星系来的光是在几百万年之前发出的，这样当我们看到宇宙时，我们是在看它的过去。",
            "如果只用一种方式了解某样事物，你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
    data_new = []
    for sentence in data:
        data_new.append(cut_word(sentence))
    # 2.实例化一个转换器类
    transfer = TfidfVectorizer(stop_words=["一种"])
    # 3.调用fit_transform
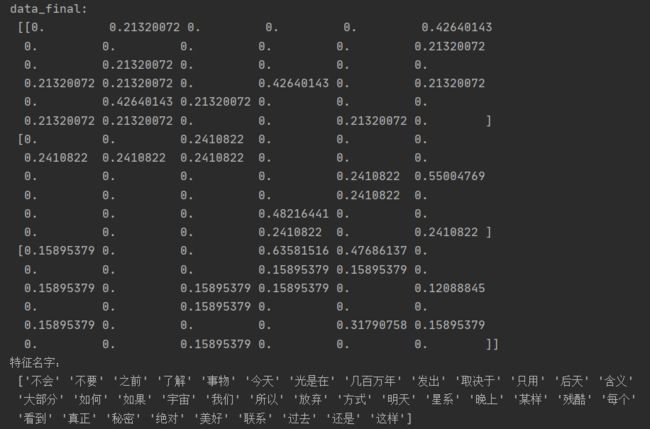
    data_final = transfer.fit_transform(data_new)
    print("data_final:\n", data_final.toarray())
    print("特征名字：\n", transfer.get_feature_names_out())
    return None

3.特征预处理

1 什么是特征预处理

1.1 特征预处理定义

scikit-learn的解释

provides several common utility functions and transformer classes to change raw feature vectors into a representation that is more suitable for the downstream estimators.

翻译过来：通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程

• 为什么我们要进行归一化/标准化？

• 特征的单位或者大小相差较大，或者某特征的方差相比其他的特征要大出几个数量级，容易影响（支配）目标结果，使得一些算法无法学习到其它的特征

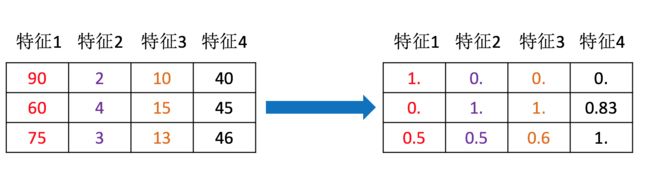
• 举例：约会对象数据

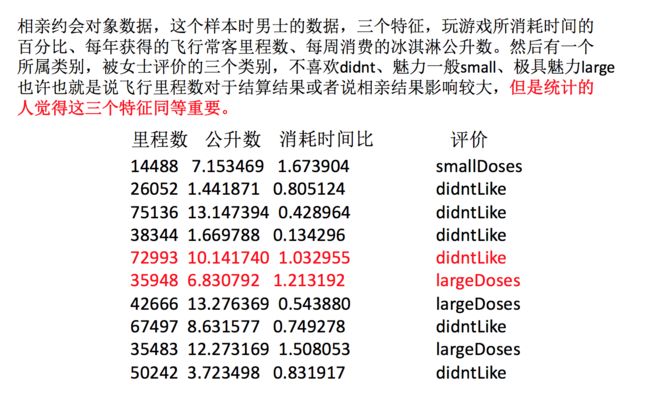
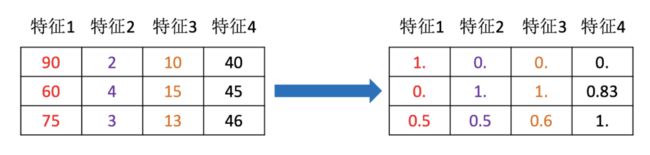
我们需要用到一些方法进行无量纲化，使不同规格的数据转换到同一规格即：

• 归一化
• 标准化

2.归一化

2.1 定义

​ 通过对原始数据进行变换把数据映射到(默认为[0,1])之间

2.2 公式

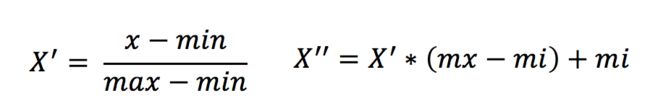
作用于每一列，max为一列的最大值，min为一列的最小值,那么X’’为最终结果，

mx，mi分别为指定区间值默认mx为1,mi为0

那么怎么理解这个过程呢？我们通过一个例子

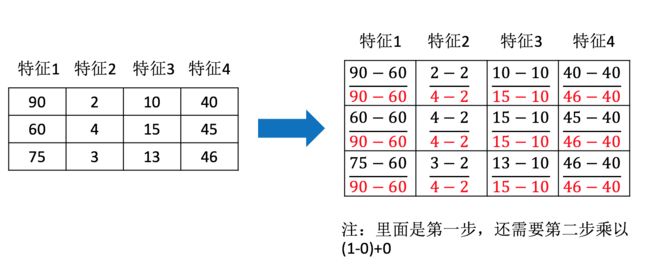
API

• sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )
  • MinMaxScalar.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
  • 返回值：转换后的形状相同的array

from sklearn.preprocessing import MinMaxScaler
import pandas as pd
# MinMaxScaler（） 归一化
def minmax_demo():
    '''
    归一化
    :return:
    '''
    # 1.获取数据
    data = pd.read_csv("../../resource/dating.txt")
    data = data.iloc[:, :3]
    print("data:\n", data)
    # 2.实例化一个转换器类 feature_range=[2,3]生成的值在2-3之间 默认不设置在0-1之间
    transfer = MinMaxScaler(feature_range=[2, 3])
    # 3.代用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new)
    return None

问题：如果数据中异常点较多，会有什么影响？

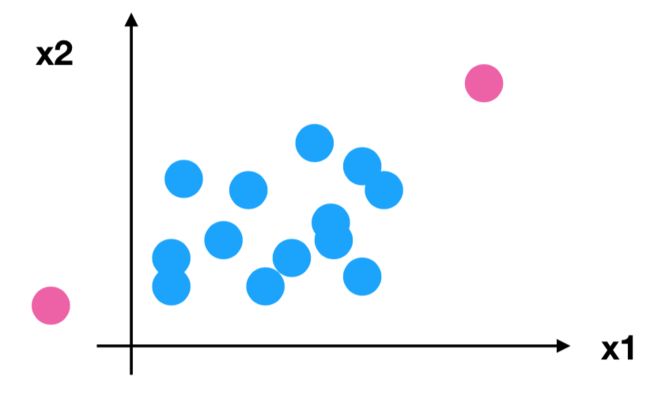
2.5 归一化总结

注意最大值最小值是变化的，另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。

怎么办？所以一般不用归一化，而是用标准化

3.标准化

定义

​ 通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内

公式

​

作用于每一列，mean为平均值，σ为标准差

所以回到刚才异常点的地方，我们再来看看标准化

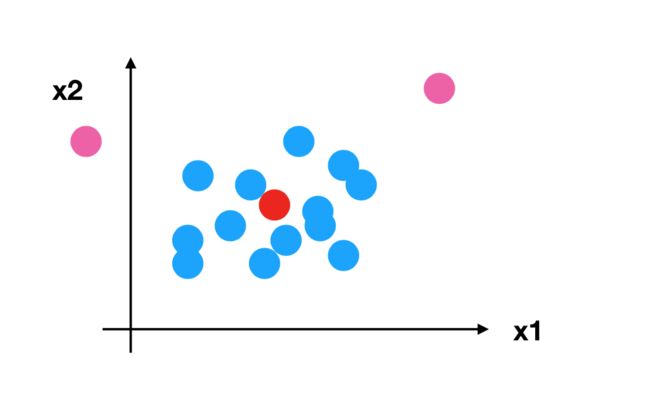
• 对于归一化来说：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变
• 对于标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小。

API

​ sklearn.preprocessing.StandardScaler( )

• 处理之后每列来说所有数据都聚集在均值0附近标准差差为1
• StandardScaler.fit_transform(X)
  • X:numpy array格式的数据[n_samples,n_features]
• 返回值：转换后的形状相同的array

# StandardScaler 标准化
from sklearn.preprocessing import StandardScaler
import pandas as pd
def stand_demo():
    '''
    标准化
    :return:
    '''
    # 1.获取数据
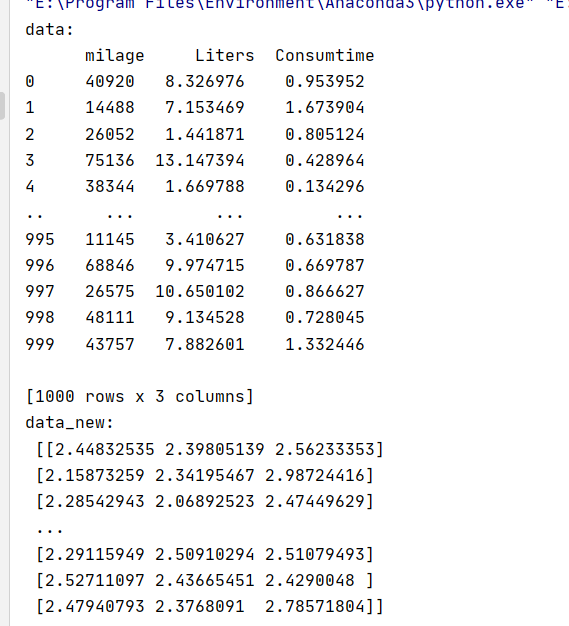
    data = pd.read_csv("../../resource/dating.txt")
    data = data.iloc[:, :3]
    print("data:\n", data)
    # 2.实例化一个转换器类
    transfer = StandardScaler()
    # 3.代用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new)

    return None

标准化总结

在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

4 总结

• 什么是特征工程【知道】
  • 定义
    • 通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程
  • 包含内容:
    • 归一化
    • 标准化
• 归一化【知道】
  • 定义:
    • 对原始数据进行变换把数据映射到(默认为[0,1])之间
  • api:
    • sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )
    • 参数:feature_range – 自己指定范围,默认0-1
  • 总结:
    • 鲁棒性比较差(容易受到异常点的影响)
    • 只适合传统精确小数据场景(以后不会用你了)
• 标准化【掌握】
  • 定义:
    • 对原始数据进行变换把数据变换到均值为0,标准差为1范围内
  • api:
    • sklearn.preprocessing.StandardScaler( )
  • 总结:
    • 异常值对我影响小
    • 适合现代嘈杂大数据场景(以后就是用你了)

4. 特征降维

ndarray
维数：嵌套的层数
0维 标量
1维 向量
2维 矩阵
3维
n维
二维数组
此处的降维：
降低特征的个数
效果：
特征与特征之间不相关

1. 降维

​ 降维是指在某些限定条件下，降低随机变量(特征)个数，得到一组“不相关”主变量的过程

• 降低随机变量的个数

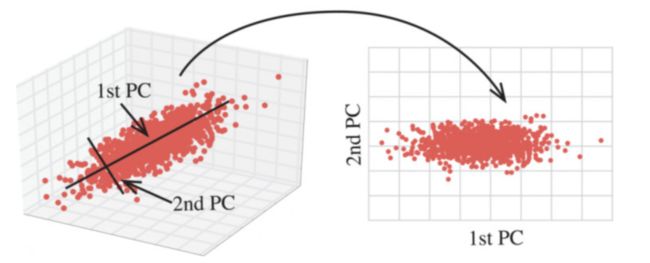
• 相关特征(correlated feature)
  • 相对湿度与降雨量之间的相关
  • 等等

正是因为在进行训练的时候，我们都是使用特征进行学习。如果特征本身存在问题或者特征之间相关性较强，对于算法学习预测会影响较大

2 降维的两种方式

• 特征选择
• 主成分分析（可以理解一种特征提取的方式）

2.特征选择

1.定义

​ 数据中包含冗余或无关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。

2 方法

• Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间关联
  • 方差选择法：低方差特征过滤
  • 相关系数
• Embedded (嵌入式)：算法自动选择特征（特征与目标值之间的关联）
  • 决策树:信息熵、信息增益
  • 正则化：L1、L2
  • 深度学习：卷积等

对于Embedded方式，只能在讲解算法的时候在进行介绍，更好的去理解

3.过滤式

低方差特征过滤

删除低方差的一些特征，前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。

• 特征方差小：某个特征大多样本的值比较相近
• 特征方差大：某个特征很多样本的值都有差别

API

• sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
  • 删除所有低方差特征
  • Variance.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
    • 返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

4 相关系数

• 皮尔逊相关系数(Pearson Correlation Coefficient)
  • 反映变量之间相关关系密切程度的统计指标

公式计算案例(了解，不用记忆)

• 公式

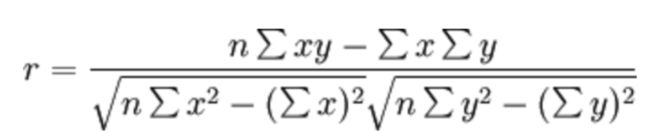
• 比如说我们计算年广告费投入与月均销售额

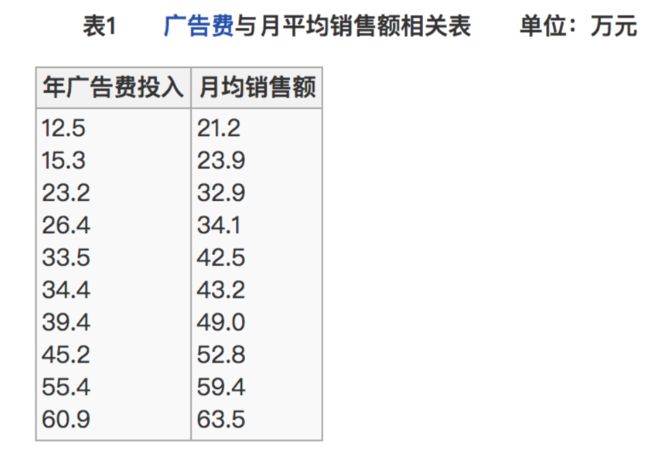
那么之间的相关系数怎么计算

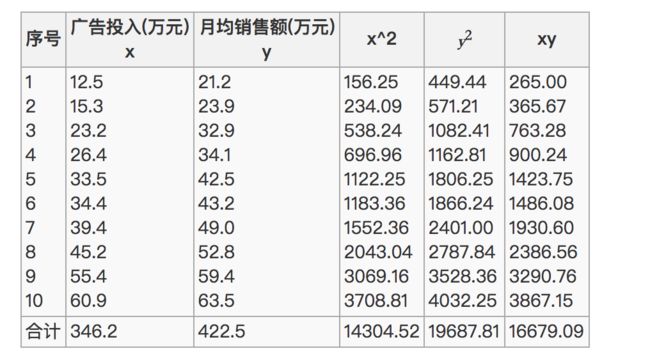
最终计算：

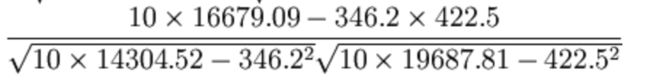
= 0.9942

所以我们最终得出结论是广告投入费与月平均销售额之间有高度的正相关关系。

特点

相关系数的值介于–1与+1之间，即–1≤ r ≤+1。其性质如下：

• 当r>0时，表示两变量正相关，r<0时，两变量为负相关
• 当|r|=1时，表示两变量为完全相关，当r=0时，表示两变量间无相关关系
• 当0<|r|<1时，表示两变量存在一定程度的相关。且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱
• 一般可按三级划分：|r|<0.4为低度相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关

这个符号：|r|为r的绝对值， |-5| = 5

API

• from scipy.stats import pearsonr
  • x : (N,) array_like
  • y : (N,) array_like Returns: (Pearson’s correlation coefficient, p-value)

案例：股票的财务指标相关性计算

from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
# VarianceThreshold() 过滤式  删除低方差特征：删除相性大的特征 相关系数（-1,1）
def variance_demo():
    '''
    过滤低方差特征
    :return:
    '''
    # 1.获取数据
    data = pd.read_csv("../../resource/factor_returns.csv")
    data = data.iloc[:, 1:-2]
    print("data:\n", data, "\n", data.shape)
    # 2.实例化一个转换器类   训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。
    transfer = VarianceThreshold(threshold=10)
    # 3.调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new, "\n", data_new.shape)
    # 计算某两个变量之间的相关系数
    factor = []
    for title in data:
        factor.append(title)
    for i in range(len(factor)):
        for j in range(i, len(factor) - 1):
            if i != j:
                r = pearsonr(data[factor[i]], data[factor[j]])
                print("%s与%s的相关性是%f" % (factor[i], factor[j], r[0]))

    r1 = pearsonr(data["pe_ratio"], data["pb_ratio"])
    print("pe_ratio与pb_ratio的相关性是\n", r1)
    # r2 = pearsonr(data["revenue"], data["total_expense"])
    # print("revenue与total_expense的相关性是\n",r2)

    return None

#返回结果
data:
       pe_ratio  pb_ratio  ...       revenue  total_expense
0       5.9572    1.1818  ...  2.070140e+10   1.088254e+10
1       7.0289    1.5880  ...  2.930837e+10   2.378348e+10
2    -262.7461    7.0003  ...  1.167983e+07   1.203008e+07
3      16.4760    3.7146  ...  9.189387e+09   7.935543e+09
4      12.5878    2.5616  ...  8.951453e+09   7.091398e+09
...        ...       ...  ...           ...            ...
2313   25.0848    4.2323  ...  1.148170e+10   1.041419e+10
2314   59.4849    1.6392  ...  1.731713e+09   1.089783e+09
2315   39.5523    4.0052  ...  1.789082e+10   1.749295e+10
2316   52.5408    2.4646  ...  6.465392e+09   6.009007e+09
2317   14.2203    1.4103  ...  4.509872e+10   4.132842e+10

[2318 rows x 9 columns] 
 (2318, 9)
data_new:
 [[ 5.95720000e+00  8.52525509e+10  8.00800000e-01 ...  1.21144486e+12
   2.07014010e+10  1.08825400e+10]
 [ 7.02890000e+00  8.41133582e+10  1.64630000e+00 ...  3.00252062e+11
   2.93083692e+10  2.37834769e+10]
 [-2.62746100e+02  5.17045520e+08 -5.67800000e-01 ...  7.70517753e+08
   1.16798290e+07  1.20300800e+07]
 ...
 [ 3.95523000e+01  1.70243430e+10  3.34400000e+00 ...  2.42081699e+10
   1.78908166e+10  1.74929478e+10]
 [ 5.25408000e+01  3.28790988e+10  2.74440000e+00 ...  3.88380258e+10
   6.46539204e+09  6.00900728e+09]
 [ 1.42203000e+01  5.91108572e+10  2.03830000e+00 ...  2.02066110e+11
   4.50987171e+10  4.13284212e+10]] 
 (2318, 7)
pe_ratio与pb_ratio的相关性是-0.004389
pe_ratio与market_cap的相关性是-0.068861
pe_ratio与return_on_asset_net_profit的相关性是-0.066009
pe_ratio与du_return_on_equity的相关性是-0.082364
pe_ratio与ev的相关性是-0.046159
pe_ratio与earnings_per_share的相关性是-0.072082
pe_ratio与revenue的相关性是-0.058693
pb_ratio与market_cap的相关性是0.009336
pb_ratio与return_on_asset_net_profit的相关性是0.445381
pb_ratio与du_return_on_equity的相关性是0.291367
pb_ratio与ev的相关性是-0.183232
pb_ratio与earnings_per_share的相关性是0.198708
pb_ratio与revenue的相关性是-0.177671
market_cap与return_on_asset_net_profit的相关性是0.214774
market_cap与du_return_on_equity的相关性是0.316288
market_cap与ev的相关性是0.565533
market_cap与earnings_per_share的相关性是0.524179
market_cap与revenue的相关性是0.440653

可以用散点图，来观察结果

3.主成分分析：PAC降维

1. 什么是主成分分析(PCA)

• 定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量
• 作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
• 应用：回归分析或者聚类分析当中

对于信息一词，在决策树中会进行介绍

2计算案例理解(了解，无需记忆)

假设对于给定5个点，数据如下

(-1,-2)
(-1, 0)
( 0, 0)
( 2, 1)
( 0, 1)

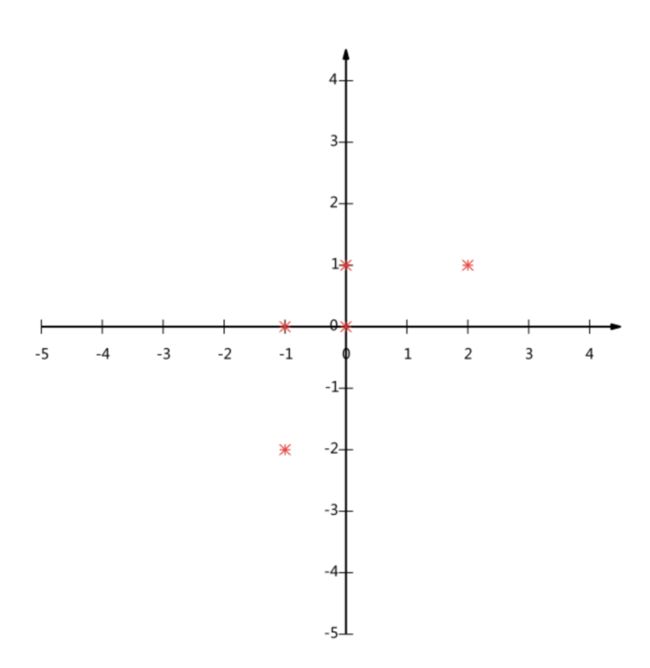
要求：将这个二维的数据简化成一维？ 并且损失少量的信息

这个过程如何计算的呢？找到一个合适的直线，通过一个矩阵运算得出主成分分析的结果（不需要理解）

API

• sklearn.decomposition.PCA(n_components=None)
  • 将数据分解为较低维数空间
  • n_components:
    • 小数：表示保留百分之多少的信息
    • 整数：减少到多少特征
  • PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]
  • 返回值：转换后指定维度的array

# 主成分分析 PCA降维过程中尽可能保留比较多的信息
def pca_demo():
    '''
    pca降维
    :return:
    '''
    # 1、获取数据
    data = [[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]
    # 2.实例化一个转换器 n_components=0.95降维保留95%的数据，n_components=2 降为2维
    transform = PCA(n_components=0.95)
    # 3.调用fit_transform
    data_new = transform.fit_transform(data)
    print("data_new:\n", data_new)
    return None

4.案例：探究用户对物品类别的喜好细分降维

数据如下：

• order_products__prior.csv：订单与商品信息
  • 字段：order_id, product_id, add_to_cart_order, reordered
• products.csv：商品信息
  • 字段：product_id, product_name, aisle_id, department_id
• orders.csv：用户的订单信息
  • 字段：order_id,user_id,eval_set,order_number,….
• aisles.csv：商品所属具体物品类别
  • 字段： aisle_id, aisle

1 需求

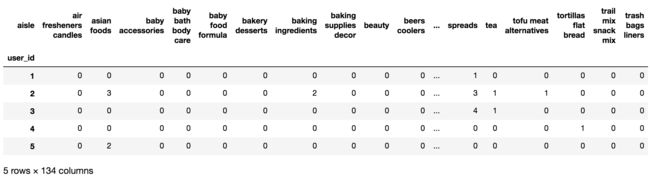
2 分析

• 合并表，使得user_id与aisle在一张表当中
• 进行交叉表变换
• 进行降维

3 完整代码

import pandas as pd
from sklearn.decomposition import PCA

# 1、获取数据集
# ·商品信息- products.csv：
# Fields：product_id, product_name, aisle_id, department_id
# ·订单与商品信息- order_products__prior.csv：
# Fields：order_id, product_id, add_to_cart_order, reordered 
# ·用户的订单信息- orders.csv：
# Fields：order_id, user_id,eval_set, order_number,order_dow, order_hour_of_day, days_since_prior_order 
# ·商品所属具体物品类别- aisles.csv：
# Fields：aisle_id, aisle     
products = pd.read_csv("./instacart/products.csv")
order_products = pd.read_csv("./instacart/order_products__prior.csv")
orders = pd.read_csv("./instacart/orders.csv")
aisles = pd.read_csv("./instacart/aisles.csv")

# 2、合并表，将user_id和aisle放在一张表上
# 1）合并orders和order_products on=order_id tab1:order_id, product_id, user_id
tab1 = pd.merge(orders, order_products, on=["order_id", "order_id"])
# 2）合并tab1和products on=product_id tab2:aisle_id
tab2 = pd.merge(tab1, products, on=["product_id", "product_id"])
# 3）合并tab2和aisles on=aisle_id tab3:user_id, aisle
tab3 = pd.merge(tab2, aisles, on=["aisle_id", "aisle_id"])

# 3、交叉表处理，把user_id和aisle进行分组
table = pd.crosstab(tab3["user_id"], tab3["aisle"])

# 4、主成分分析的方法进行降维
# 1）实例化一个转换器类PCA
transfer = PCA(n_components=0.95)
# 2）fit_transform
data = transfer.fit_transform(table)

data.shape

返回结果：

(206209, 44)

3.总结

小问题

1、数据集的结构是什么?

答案: 特征值+ 目标值

2、机器学习算法分成哪些类别? 如何分类

答案: 根据是否有目标值分为 监督学习和非监督学习监督学习

​ 根据目标值的数据类型:目标值为离散值就是分类问题

​ 目标值为连续值就是回归问题

3、什么是标准化? 和归一化相比有什么优点?

答案: 标准化是通过对原始数据进行变换把数据变换到均值为0,方差为1范围内

​ 优点: 少量异常点, 不影响平均值和方差, 对转换影响小