机器学习算法系列(七)-对数几率回归算法(一)(Logistic Regression Algorithm)
阅读本文需要的背景知识点:线性回归、最大似然估计、一丢丢编程知识
一、引言
前面几节我们学习了标准线性回归,然后介绍了三种正则化的方法 - 岭回归、Lasso回归、弹性网络回归,这些线性模型解决的都是回归的问题。最开始还介绍了两种简单的算法-PLA与口袋算法,他们解决的是分类问题。
那么我们能使用回归的方式来解决分类问题么,答案是肯定的,这就是下面要介绍的模型 - 对数几率回归算法1(Logistic Regression Algorithm),也有被直译为逻辑回归。
二、模型介绍
对数几率回归的模型函数
既然要通过回归的方式来解决分类的问题,可以通过先进行回归分析,然后通过一个函数将连续的结果映射成离散的分类结果,例如下面的函数表达式:
y = { 0 ( f ( w T x ) ≤ C ) 1 ( f ( w T x ) > C ) y=\left\{\begin{array}{ll} 0 & \left(f\left(w^{T} x\right) \leq C\right) \\ 1 & \left(f\left(w^{T} x\right)>C\right) \end{array}\right. y={01(f(wTx)≤C)(f(wTx)>C)
在介绍对数几率回归模型之前,先来看看一类被称为 S 函数2(Sigmoid function)的函数,这类函数的图像成 S 型,其中最常见的一种函数为逻辑函数3(Logistic function),函数图像如下图所示:
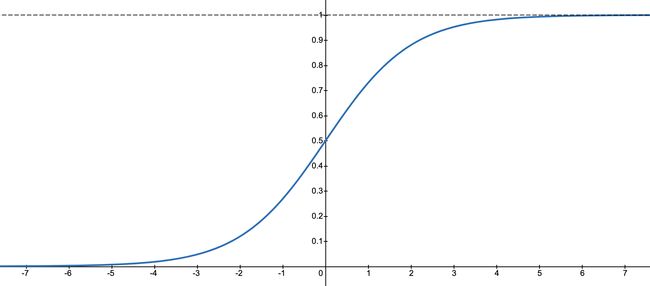
通过图像可以看到,这个函数当自变量越大时,函数值越趋近于 1,当自变量最小时,函数值越趋近于 0,当自变量为 0 时,函数值为 0.5。当上面表达式中的 C 等于 0.5 时,可以看作将连续的结果映射成离散的结果。
逻辑函数的函数表达式为:
f ( z ) = 1 1 + e − z f(z)=\frac{1}{1+e^{-z}} f(z)=1+e−z1
将线性方程带入逻辑函数中,就得到了对数几率回归的函数方程:
f ( x ) = 1 1 + e − w T x f(x)=\frac{1}{1+e^{-w^Tx}} f(x)=1+e−wTx1
对数几率回归的代价函数
我们需要一个代价函数来表示数据拟合的情况,这时很容易想到的是使用与线性回归一样的均方差4(mean-square error / MSE)的方法来做为代价函数
Cost ( w ) = ∑ i = 1 N ( y − y ^ ) 2 \operatorname{Cost}(w)=\sum_{i=1}^{N}(y-\hat{y})^{2} Cost(w)=i=1∑N(y−y^)2
但对数几率回归是使用似然函数5(likelihood function)的对数形式来作为其代价函数,后面会说明为什么使用这种方式比MSE更合适。
最大似然估计:
考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次(正面记为H,反面记为T)。并把抛出一个正面的概率记为 p,抛出一个反面的概率记为 1 - p。假设我们抛出了49个正面,31个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为 1/3、1/2、2/3 。这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,基于二项分布中的概率质量函数公式,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。我们可以看到当 p = 2/3 时,似然函数取得值最大。
L ( p = 1 3 ∣ H = 49 , T = 31 ) = C 80 49 ( 1 3 ) 49 ( 1 − 1 3 ) 31 ≈ 0.000 L ( p = 1 2 ∣ H = 49 , T = 31 ) = C 80 49 ( 1 2 ) 49 ( 1 − 1 2 ) 31 ≈ 0.012 L ( p = 2 3 ∣ H = 49 , T = 31 ) = C 80 49 ( 2 3 ) 49 ( 1 − 2 3 ) 31 ≈ 0.054 \begin{array}{l} L\left(p=\frac{1}{3} \mid H=49, T=31\right)=C_{80}^{49}\left(\frac{1}{3}\right)^{49}\left(1-\frac{1}{3}\right)^{31} \approx 0.000 \\ L\left(p=\frac{1}{2} \mid H=49, T=31\right)=C_{80}^{49}\left(\frac{1}{2}\right)^{49}\left(1-\frac{1}{2}\right)^{31} \approx 0.012 \\ L\left(p=\frac{2}{3} \mid H=49, T=31\right)=C_{80}^{49}\left(\frac{2}{3}\right)^{49}\left(1-\frac{2}{3}\right)^{31} \approx 0.054 \end{array} L(p=31∣H=49,T=31)=C8049(31)49(1−31)31≈0.000L(p=21∣H=49,T=31)=C8049(21)49(1−21)31≈0.012L(p=32∣H=49,T=31)=C8049(32)49(1−32)31≈0.054
第一种表示方式:
在二元分类的情况下,例如 y 取 0 或者 1,将对数几率回归的函数方程的结果看作概率,可以写作下式:
{ P ( y = 1 ∣ x , w ) = h ( x ) P ( y = 0 ∣ x , w ) = 1 − h ( x ) \left\{\begin{array}{ll} P(y=1 \mid x, w)= & h(x) \\ P(y=0 \mid x, w)= & 1-h(x) \end{array}\right. {P(y=1∣x,w)=P(y=0∣x,w)=h(x)1−h(x)
由于 y 只能取 0 或者 1,可以将上面两个式写成一个式子:
P ( y ∣ x , w ) = h ( x ) y [ 1 − h ( x ) ] 1 − y P(y \mid x, w)=h(x)^{y}[1-h(x)]^{1-y} P(y∣x,w)=h(x)y[1−h(x)]1−y
写出似然函数,其中 N 为样本总数量,将每一个概率累乘就得到了似然函数:
L ( w ) = ∏ i = 1 N h ( X i ) y i [ 1 − h ( X i ) ] 1 − y i L(w)=\prod_{i=1}^{N} h\left(X_{i}\right)^{y_{i}}\left[1-h\left(X_{i}\right)\right]^{1-y_{i}} L(w)=i=1∏Nh(Xi)yi[1−h(Xi)]1−yi
在 w 的所有可能取值中找一个使得似然函数取到最大值,这时求得的解就是 w 的最大似然估计6(maximum likelihood estimation/MLE)
w = argmax w ( L ( w ) ) = argmax w ( ∏ i = 1 N h ( X i ) y i [ 1 − h ( X i ) ] 1 − y i ) w=\underset{w}{\operatorname{argmax}}(L(w))=\underset{w}{\operatorname{argmax}}\left(\prod_{i=1}^{N} h\left(X_{i}\right)^{y_{i}}\left[1-h\left(X_{i}\right)\right]^{1-y_{i}}\right) w=wargmax(L(w))=wargmax(i=1∏Nh(Xi)yi[1−h(Xi)]1−yi)
由于带连乘运算的代价函数不好优化,这里我们对似然函数取自然对数并且取反,S 函数的取值为(0,1),似然函数的取值也是(0,1),对其取对数不影响其单调性。这样就得到了对数几率回归的代价函数:
Cost ( w ) = − ln L ( w ) = − ∑ i = 1 N ( y i ln h ( X i ) + ( 1 − y i ) ln ( 1 − h ( X i ) ) ) \begin{aligned} \operatorname{Cost}(w) &=-\ln L(w) \\ &=-\sum_{i=1}^{N}\left(y_{i} \ln h\left(X_{i}\right)+\left(1-y_{i}\right) \ln \left(1-h\left(X_{i}\right)\right)\right) \end{aligned} Cost(w)=−lnL(w)=−i=1∑N(yilnh(Xi)+(1−yi)ln(1−h(Xi)))
由于加了一步取反的操作,这是就不是求最大值,而是将其改为求最小值:
w = argmin w ( − ∑ i = 1 N ( y i ln h ( X i ) + ( 1 − y i ) ln ( 1 − h ( X i ) ) ) ) w=\underset{w}{\operatorname{argmin}}\left(-\sum_{i=1}^{N}\left(y_{i} \ln h\left(X_{i}\right)+\left(1-y_{i}\right) \ln \left(1-h\left(X_{i}\right)\right)\right)\right) w=wargmin(−i=1∑N(yilnh(Xi)+(1−yi)ln(1−h(Xi))))
第二种表示方式:
我们先来看下 S 函数的一个性质:
f ( z ) = 1 1 + e − z = e z 1 + e z f ( − z ) = 1 1 + e z = 1 − f ( z ) \begin{aligned} f(z) &=\frac{1}{1+e^{-z}}=\frac{e^{z}}{1+e^{z}} \\ f(-z) &=\frac{1}{1+e^{z}}=1-f(z) \end{aligned} f(z)f(−z)=1+e−z1=1+ezez=1+ez1=1−f(z)
在二元分类的情况下, 当 y 的值取 -1 或者 1 时,将对数几率回归的函数方程的结果看作概率,可以写作下式
{ P ( y = 1 ∣ x , w ) = h ( x ) = 1 1 + e − w T x P ( y = − 1 ∣ x , w ) = 1 − h ( x ) = h ( − x ) = 1 1 + e w T x \left\{\begin{array}{l} P(y=1 \mid x, w)=h(x)=\frac{1}{1+e^{-w^{T} x}} \\ P(y=-1 \mid x, w)=1-h(x)=h(-x)=\frac{1}{1+e^{w^{T} x}} \end{array}\right. {P(y=1∣x,w)=h(x)=1+e−wTx1P(y=−1∣x,w)=1−h(x)=h(−x)=1+ewTx1
由于 y 只能取 -1 或者 1,可以将上面两个式写成一个式子:
P ( y ∣ x , w ) = 1 1 + e − y w T x P(y \mid x, w)=\frac{1}{1+e^{-y w^{T} x}} P(y∣x,w)=1+e−ywTx1
写出似然函数,其中 N 为样本总数量,将每一个概率累乘就得到了似然函数:
L ( w ) = ∏ i = 1 N 1 1 + e − y i w T X i L(w)=\prod_{i=1}^{N} \frac{1}{1+e^{-y_{i} w^{T} X_{i}}} L(w)=i=1∏N1+e−yiwTXi1
还是求最大似然估计:
w = argmax w ( ∏ i = 1 N 1 1 + e − y i w T X i ) w=\underset{w}{\operatorname{argmax}}\left(\prod_{i=1}^{N} \frac{1}{1+e^{-y_{i} w^{T} X_{i}}}\right) w=wargmax(i=1∏N1+e−yiwTXi1)
这里与第一种方式一样,我们对似然函数取自然对数并且取反,就得到了对数几率回归的代价函数:
Cost ( w ) = − ln L ( w ) = − ∑ i = 1 N ln 1 1 + e − y i w T X i = − ∑ i = 1 N ln 1 − ln ( 1 + e − y i w T X i ) = ∑ i = 1 N ln ( 1 + e − y i w T X i ) \begin{aligned} \operatorname{Cost}(w) &=-\ln L(w) \\ &=-\sum_{i=1}^{N} \ln \frac{1}{1+e^{-y_{i} w^{T} X_{i}}} \\ &=-\sum_{i=1}^{N} \ln 1-\ln \left(1+e^{-y_{i} w^{T} X_{i}}\right) \\ &=\sum_{i=1}^{N} \ln \left(1+e^{-y_{i} w^{T} X_{i}}\right) \end{aligned} Cost(w)=−lnL(w)=−i=1∑Nln1+e−yiwTXi1=−i=1∑Nln1−ln(1+e−yiwTXi)=i=1∑Nln(1+e−yiwTXi)
也是求代价函数的最小值:
w = argmin w ( ∑ i = 1 N ln ( 1 + e − y i w T X i ) ) w=\underset{w}{\operatorname{argmin}}\left(\sum_{i=1}^{N} \ln \left(1+e^{-y_{i} w^{T} X_{i}}\right)\right) w=wargmin(i=1∑Nln(1+e−yiwTXi))
在 sklearn 中使用的就是上面这个代价函数。
对数几率回归的正则化:
与线性回归一样,对数几率回归的代价函数也可以加上正则化的惩罚项,有两种方式来添加正则项,一个是给正则项添加系数来控制大小,另一个是给代价函数添加系数来控制大小,本质作用是一样的,在 sklearn 中使用的是(2)式中的形式。
L1 正则化:
Cost ( w ) L 1 = Cost ( w ) + λ ∥ w ∥ 1 ( 1 ) = C ⋅ Cost ( w ) + ∥ w ∥ 1 ( 2 ) \begin{aligned} \operatorname{Cost}(w)_{L 1} &=\operatorname{Cost}(w)+\lambda\|w\|_{1} & (1) \\ &=C \cdot \operatorname{Cost}(w)+\|w\|_{1} & (2) \end{aligned} Cost(w)L1=Cost(w)+λ∥w∥1=C⋅Cost(w)+∥w∥1(1)(2)
L2 正则化:
Cost ( w ) L 2 = Cost ( w ) + λ ∥ w ∥ 2 2 ( 1 ) = C ⋅ Cost ( w ) + ∥ w ∥ 2 2 ( 2 ) \begin{aligned} \operatorname{Cost}(w)_{L2} &=\operatorname{Cost}(w)+\lambda\|w\|_{2}^2 & (1) \\ &=C \cdot \operatorname{Cost}(w)+\|w\|_{2}^2 & (2) \end{aligned} Cost(w)L2=Cost(w)+λ∥w∥22=C⋅Cost(w)+∥w∥22(1)(2)
弹性网络正则化:
Cost ( w ) E N = Cost ( w ) + λ ρ ∥ w ∥ 1 + λ ( 1 − ρ ) 2 ∥ w ∥ 2 2 = C ⋅ Cost ( w ) + ρ ∥ w ∥ 1 + ( 1 − ρ ) 2 ∥ w ∥ 2 2 \begin{aligned} \operatorname{Cost}(w)_{E N} &=\operatorname{Cost}(w)+\lambda \rho\|w\|_{1}+\frac{\lambda(1-\rho)}{2}\|w\|_{2}^{2} \\ &=C \cdot \operatorname{Cost}(w)+\rho\|w\|_{1}+\frac{(1-\rho)}{2}\|w\|_{2}^{2} \end{aligned} Cost(w)EN=Cost(w)+λρ∥w∥1+2λ(1−ρ)∥w∥22=C⋅Cost(w)+ρ∥w∥1+2(1−ρ)∥w∥22
对数几率回归的代价函数最小化的优化方法有多种,例如前面几节介绍过的坐标下降法。无正则化或者L2正则化的情况下可以用梯度下降法7 (Gradient descent)、牛顿法8 (Newton’s method)来等等。
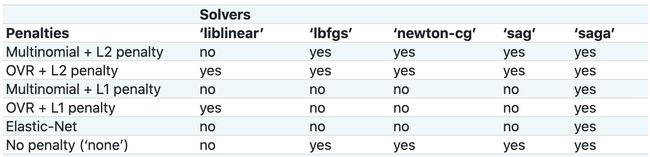
在 scikit-learn 中可以看到更多的优化方法,其中大多是前面提到算法的加速版本或是变体,例如随机平均梯度下降法(Stochastic Average Gradient / SAG)、随机平均梯度下降加速法(SAGA)、L-BFGS算法(Limited-memory Broyden–Fletcher–Goldfarb–Shanno / L-BFGS),后面会逐个介绍这些算法。
三、算法步骤
梯度下降法
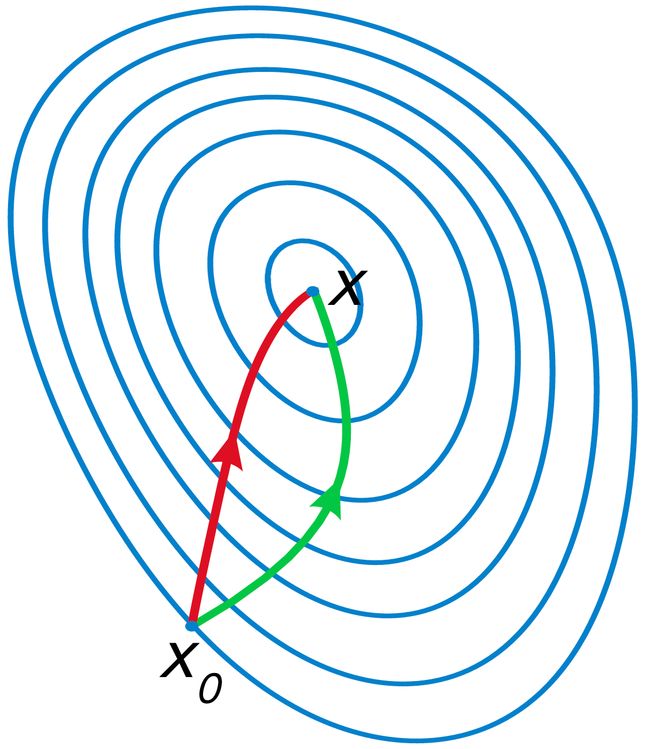
梯度下降法与坐标下降法的思路一样,都是通过一次一次更新权重系数 w,一步一步的逼近代价函数的最小值。坐标下降法是通过固定某一个坐标轴,求出局部最优解,然后更新 w 的值。梯度下降法则是求出函数的梯度后,沿着梯度的反方向再找到一个合适的步长系数迭代更新 w 的值。
可以理解为碗中的一个小球从某一点自由滚落,必然会沿着变化量最大的方向移动,最后到达最低点。
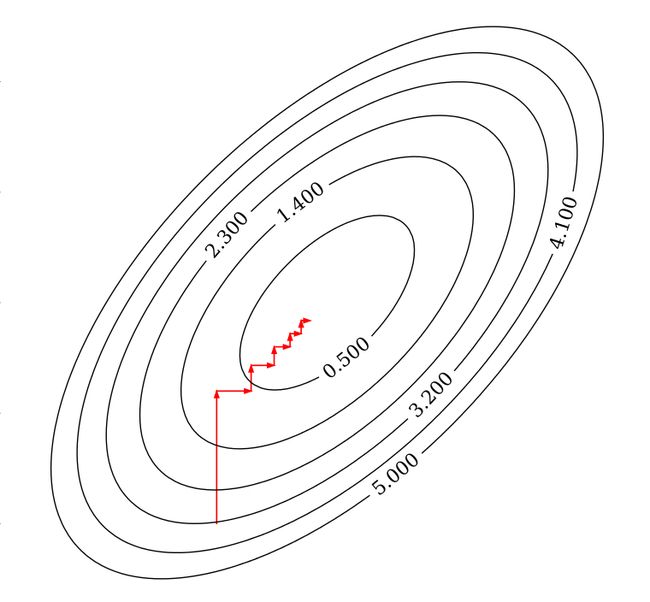
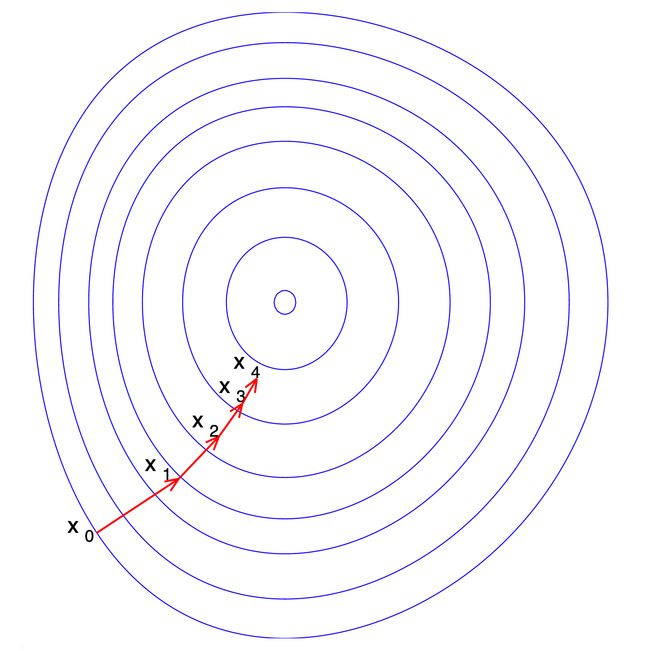
具体步骤:
(1)初始化权重系数 w,例如初始化为零向量
(2)计算下降方向,梯度下降法将梯度的反方向作为下降方向
Δ w = − ∂ Cost ( w ) ∂ w \Delta w = -\frac{\partial \operatorname{Cost}(w) }{\partial w} Δw=−∂w∂Cost(w)
(3)使用线搜索9 方法来计算下降的步长 α,以使每一步迭代都满足Wolfe条件10
(4)更新权重系数 w
w = w + α Δ w w=w+\alpha \Delta w w=w+αΔw
(5)重复步骤(2)~(4)直到梯度的大小足够小
牛顿法
牛顿法与梯度下降法一样,也是一种下降方法,两个算法的步骤大致相同,区别就在于选择的下降方向不一样。
具体步骤:
(1)初始化权重系数 w,例如初始化为零向量
(2)计算下降方向,牛顿法使用二阶泰勒展开,将黑塞矩阵的逆矩阵与梯度的乘积的反方向作为下降方向
Δ w = − H − 1 ∂ Cost ( w ) ∂ w \Delta w=-H^{-1} \frac{\partial \operatorname{Cost}(w)}{\partial w} Δw=−H−1∂w∂Cost(w)
(3)使用线搜索9 方法来计算下降的步长 α,以使每一步迭代都满足Wolfe条件10
(4)更新权重系数 w
w = w + α Δ w w=w+\alpha \Delta w w=w+αΔw
(5)重复步骤(2)~(4)直到梯度的大小足够小
四、原理证明
对数几率回归的代价函数是凸函数
凸函数除了通过前面几节中介绍的方法判断外,如果函数是二阶可导的,当函数的黑塞矩阵是半正定的,该函数就为凸函数。
多元二次可微的连续函数在凸集上是凸的,当且仅当它的黑塞矩阵在凸集的内部是半正定的。
- 第一种代价函数:
(1)将代价函数连加运算去掉得到一个新函数
(2)带入 h(x)
(3)将 e 的指数符号变换一下
(4)对数除法展开为对数的减法
(5)展开括号
(6)第二项与第四项一样,化简得到
f ( w ) = − ( y ln h ( x ) + ( 1 − y ) ln ( 1 − h ( x ) ) ) ( 1 ) = − ( y ln 1 1 + e − w T x + ( 1 − y ) ln ( 1 − 1 1 + e − w T x ) ) ( 2 ) = − ( y ln e w T x 1 + e w T x + ( 1 − y ) ln ( 1 1 + e w T x ) ) ( 3 ) = − y ( w T x − ln ( 1 + e w T x ) ) − ( 1 − y ) ( 0 − ln ( 1 + e w T x ) ) ( 4 ) = − y w T x + y ( 1 + e w T x ) + ln ( 1 + e w T x ) − y ( 1 + e w T x ) ( 5 ) = ln ( 1 + e w T x ) − y w T x ( 6 ) \begin{aligned} f(w) &=-(y \ln h(x)+(1-y) \ln (1-h(x))) & (1)\\ &=-\left(y \ln \frac{1}{1+e^{-w^{T} x}}+(1-y) \ln \left(1-\frac{1}{1+e^{-w^{T} x}}\right)\right) & (2)\\ &=-\left(y \ln \frac{e^{w^{T} x}}{1+e^{w^{T} x}}+(1-y) \ln \left(\frac{1}{1+e^{w^{T} x}}\right)\right) & (3)\\ &=-y\left(w^{T} x-\ln \left(1+e^{w^{T} x}\right)\right)-(1-y)\left(0-\ln \left(1+e^{w^{T} x}\right)\right) & (4) \\ &=-y w^{T} x+y\left(1+e^{w^{T} x}\right)+\ln \left(1+e^{w^{T} x}\right)-y\left(1+e^{w^{T} x}\right) & (5)\\ &=\ln \left(1+e^{w^{T} x}\right)-y w^{T} x & (6) \end{aligned} f(w)=−(ylnh(x)+(1−y)ln(1−h(x)))=−(yln1+e−wTx1+(1−y)ln(1−1+e−wTx1))=−(yln1+ewTxewTx+(1−y)ln(1+ewTx1))=−y(wTx−ln(1+ewTx))−(1−y)(0−ln(1+ewTx))=−ywTx+y(1+ewTx)+ln(1+ewTx)−y(1+ewTx)=ln(1+ewTx)−ywTx(1)(2)(3)(4)(5)(6)
(1)上面得到的 f(w)
(2)根据求导公式求一阶导数
(3)利用 S 函数的性质,将分子化简一下并合并同类项
(4)根据求导公式求二阶导数
(5)整理一下结果,可以看到二阶导数是一个正数乘以一个由 x 向量与 x 向量组成的矩阵
f ( w ) = ln ( 1 + e w T x ) − y w T x ( 1 ) ∂ f ( w ) ∂ w = 1 1 + e w T x e w T x x − y x ( 2 ) = ( 1 1 + e − w T x − y ) x ( 3 ) ∂ 2 f ( w ) ∂ w ∂ w T = − 1 ( 1 + e − w T x ) 2 e − w T x x ( − x T ) ( 4 ) = e − w T x ( 1 + e − w T x ) 2 x x T ( 5 ) \begin{aligned} f(w) &=\ln \left(1+e^{w^{T} x}\right)-y w^{T} x & (1)\\ \frac{\partial f(w)}{\partial w} &=\frac{1}{1+e^{w^{T} x}} e^{w^{T} x} x-y x & (2)\\ &=\left(\frac{1}{1+e^{-w^{T} x}}-y\right) x & (3)\\ \frac{\partial^{2} f(w)}{\partial w \partial w^{T}} &=-\frac{1}{\left(1+e^{-w^{T} x}\right)^{2}} e^{-w^{T} x}x(-x^{T}) & (4)\\ &=\frac{e^{-w^{T} x}}{\left(1+e^{-w^{T} x}\right)^{2}} x x^{T} & (5) \end{aligned} f(w)∂w∂f(w)∂w∂wT∂2f(w)=ln(1+ewTx)−ywTx=1+ewTx1ewTxx−yx=(1+e−wTx1−y)x=−(1+e−wTx)21e−wTxx(−xT)=(1+e−wTx)2e−wTxxxT(1)(2)(3)(4)(5)
- 第二种代价函数:
(1)将代价函数连加运算去掉得到一个新函数
(2)根据求导公式求一阶导数
(3)利用 S 函数的性质,将分子化简一下
(4)根据求导公式求二阶导数
(5)y 的平方为 1,整理一下结果,可以看到二阶导数也是一个正数乘以一个由 x 向量与 x 向量组成的矩阵
f ( w ) = ln ( 1 + e − y w T x ) ( 1 ) ∂ f ( w ) ∂ w = 1 1 + e − y w T x e − y w T x ( − y x ) ( 2 ) = − y 1 + e y w T x x ( 3 ) ∂ 2 f ( w ) ∂ w ∂ w T = y ( 1 + e y w T x ) 2 e y w T x x ( y x T ) ( 4 ) = e y w T x ( 1 + e y w T x ) 2 x x T ( 5 ) \begin{aligned} f(w) &=\ln \left(1+e^{-y w^{T} x}\right) & (1)\\ \frac{\partial f(w)}{\partial w} &=\frac{1}{1+e^{-y w^{T} x}} e^{-y w^{T} x}\left(-y x\right) & (2)\\ &=-\frac{y}{1+e^{y w^{T} x}} x & (3)\\ \frac{\partial^{2} f(w)}{\partial w \partial w^{T}} &=\frac{y}{\left(1+e^{y w^{T} x}\right)^{2}} e^{y w^{T} x} x \left(yx^{T}\right) & (4)\\ &=\frac{e^{y w^{T} x}}{\left(1+e^{y w^{T} x}\right)^{2}} x x^{T} & (5) \end{aligned} f(w)∂w∂f(w)∂w∂wT∂2f(w)=ln(1+e−ywTx)=1+e−ywTx1e−ywTx(−yx)=−1+eywTxyx=(1+eywTx)2yeywTxx(yxT)=(1+eywTx)2eywTxxxT(1)(2)(3)(4)(5)
(1)令二阶导数为 H 矩阵
(2)矩阵正定的判断方法,带入二阶导数,两种二阶导数的常数部分都用 C 表示,并且 C > 0
(3)利用转置的性质改写一下
(4)可以看到最后的结果大于等于 0,说明 H 为半正定矩阵
H = ∂ 2 f ( w ) ∂ w ∂ w T ( 1 ) v T H v = C ⋅ v T x x T v ( C > 0 ) ( 2 ) = C ⋅ ( x T v ) T ( x T v ) ( 3 ) = C ⋅ ∣ x T v ∣ 2 ≥ 0 ( 4 ) \begin{aligned} H &=\frac{\partial^{2} f(w)}{\partial w \partial w^{T}} & (1) \\ v^{T} H v &=C \cdot v^{T} x x^{T} v \quad(C>0) & (2) \\ &=C \cdot\left(x^{T} v\right)^{T}\left(x^{T} v\right) & (3) \\ &=C \cdot\left|x^{T} v\right|^{2} \geq 0 & (4) \end{aligned} HvTHv=∂w∂wT∂2f(w)=C⋅vTxxTv(C>0)=C⋅(xTv)T(xTv)=C⋅∣∣xTv∣∣2≥0(1)(2)(3)(4)
两种新函数的黑塞矩阵都是半正定的,那么新函数是凸函数,多个凸函数相加的函数依然是凸函数,则说明代价函数是一个凸函数,证毕。
为什么不用MSE作为代价函数11
- MSE 作为代价函数对错误数据的惩罚力度不足
当预测数据完全错误时(例如实际值为 0 预测值为 1,或实际值为 1 预测值为 0)
用MSE作为代价函数:
Cost = ( 1 − 0 ) 2 = 1 \text { Cost }=(1-0)^{2}=1 Cost =(1−0)2=1
使用对数似然函数作为代价函数(第一种):
Cost = − ( 1 ⋅ ln 0 + ( 1 − 1 ) ⋅ ln ( 1 − 0 ) ) = ∞ \text { Cost }=-(1 \cdot \ln 0+(1-1) \cdot \ln (1-0))=\infty Cost =−(1⋅ln0+(1−1)⋅ln(1−0))=∞
使用对数似然函数作为代价函数(第二种):
(1)实际值为 1 预测值为 -1
(2)预测值为 -1,其对应的h(x) = 0
(3)这时线性组合的值为负无穷大
(4)这时的代价为无穷大
y = 1 , y ^ = − 1 ( 1 ) h ( x ) = 0 ( 2 ) w T x = − ∞ ( 3 ) Cost = ln ( 1 + e − 1 ⋅ ( − ∞ ) ) = ∞ ( 4 ) \begin{aligned} & y=1, \hat{y}=-1 & (1)\\ &h(x)=0 & (2)\\ &w^{T} x=-\infty & (3)\\ &\text { Cost }=\ln \left(1+e^{-1 \cdot(-\infty)}\right)=\infty & (4) \end{aligned} y=1,y^=−1h(x)=0wTx=−∞ Cost =ln(1+e−1⋅(−∞))=∞(1)(2)(3)(4)
可以看到 MSE 的代价值远远小于对数似然函数的代价值,说明 MSE 的代价函数不会重重地惩罚错误分类,哪怕是完全错误的分类。
- MSE 作为代价函数不是一个凸函数
先来看下上面 S 函数导函数的一个性质,下面会用到这个性质:
h ( z ) = 1 1 + e − z ∂ h ( z ) ∂ z = − 1 ( 1 + e − z ) 2 e − z ( − 1 ) = e − z ( 1 + e − z ) 2 = 1 1 + e − z e − z 1 + e − z = h ( z ) ( 1 − h ( z ) ) \begin{aligned} h(z) &=\frac{1}{1+e^{-z}} \\ \frac{\partial h(z)}{\partial z} &=-\frac{1}{\left(1+e^{-z}\right)^{2}} e^{-z}(-1) \\ &=\frac{e^{-z}}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1}{1+e^{-z}} \frac{e^{-z}}{1+e^{-z}} \\ &=h(z)(1-h(z)) \end{aligned} h(z)∂z∂h(z)=1+e−z1=−(1+e−z)21e−z(−1)=(1+e−z)2e−z=1+e−z11+e−ze−z=h(z)(1−h(z))
(1)将 MSE 作为代价函数
(2)求一阶导数,由于直接对 w 求导较为复杂,所以拆解为两步求导
(3)先对 y ^ \hat{y} y^ 求导,后面再对 w 求导,用到了上面说的 S 函数的性质,注意最后还有一个 x
(4)展开括号
(5)求二阶导数,也是拆解为两步求导
(6)先对 y ^ \hat{y} y^ 求导,后面再对 w 求导
Cost ( w ) = ( y − y ^ ) 2 ( 1 ) ∂ Cost ( w ) ∂ w = ∂ Cost ( w ) ∂ y ^ ∂ y ^ ∂ w ( 2 ) = 2 ( y − y ^ ) ( − 1 ) y ^ ( 1 − y ^ ) x ( 3 ) = − 2 ( y y ^ − y ^ 2 − y y ^ 2 + y ^ 3 ) x ( 4 ) ∂ 2 Cost ( w ) ∂ w ∂ w T = ∂ ∂ Cost ( w ) ∂ w ∂ y ^ ∂ y ^ ∂ w T ( 5 ) = − 2 ( y − 2 y ^ − 2 y y ^ + 3 y ^ 2 ) y ^ ( 1 − y ^ ) x x T ( 6 ) \begin{aligned} \operatorname{Cost}(w) &=(y-\hat{y})^{2} & (1)\\ \frac{\partial \operatorname{Cost}(w)}{\partial w} &=\frac{\partial \operatorname{Cost}(w)}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial w} & (2)\\ &=2(y-\hat{y})(-1) \hat{y}(1-\hat{y}) x & (3)\\ &=-2\left(y \hat{y}-\hat{y}^{2}-y \hat{y}^{2}+\hat{y}^{3}\right) x & (4)\\ \frac{\partial^{2} \operatorname{Cost}(w)}{\partial w\partial w^T} &=\frac{\partial \frac{\partial \operatorname{Cost}(w)}{\partial w}}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial w^T} & (5)\\ &=-2\left(y-2 \hat{y}-2 y \hat{y}+3 \hat{y}^{2}\right) \hat{y}(1-\hat{y}) xx^{T} & (6) \end{aligned} Cost(w)∂w∂Cost(w)∂w∂wT∂2Cost(w)=(y−y^)2=∂y^∂Cost(w)∂w∂y^=2(y−y^)(−1)y^(1−y^)x=−2(yy^−y^2−yy^2+y^3)x=∂y^∂∂w∂Cost(w)∂wT∂y^=−2(y−2y^−2yy^+3y^2)y^(1−y^)xxT(1)(2)(3)(4)(5)(6)
同上面证明一样,现在只需要看常数项是否是大于等于 0
(1)当 y = 1 时,带入二阶导函数中
(2)因式分解
(3)可以看到,当 y ^ \hat{y} y^ 取不同范围的时候,常数项不是一直都是大于等于 0 的
g ( y ^ ) = − 2 ( 1 − 4 y ^ + 3 y ^ 2 ) ( y = 1 ) ( 1 ) = − 2 ( 3 y ^ − 1 ) ( y ^ − 1 ) ( 2 ) ⇒ { y ^ ∈ [ 0 , 1 3 ) g ( y ^ ) < 0 y ^ ∈ [ 1 3 , 1 ] g ( y ^ ) ≥ 0 ( 3 ) \begin{aligned} g(\hat{y}) &=-2\left(1-4 \hat{y}+3 \hat{y}^{2}\right) \quad(y=1) & (1) \\ &=-2(3 \hat{y}-1)(\hat{y}-1) & (2) \\ & \Rightarrow\left\{\begin{array}{ll} \hat{y} \in\left[0, \frac{1}{3}\right) & g(\hat{y})<0 \\ \hat{y} \in\left[\frac{1}{3}, 1\right] & g(\hat{y}) \geq 0 \end{array}\right. & (3) \end{aligned} g(y^)=−2(1−4y^+3y^2)(y=1)=−2(3y^−1)(y^−1)⇒{y^∈[0,31)y^∈[31,1]g(y^)<0g(y^)≥0(1)(2)(3)
(1)当 y = 0 时,带入二阶导函数中
(2)因式分解
(3)可以看到,当 y ^ \hat{y} y^ 取不同范围的时候,常数项也不是一直都是大于等于 0 的
g ( y ^ ) = − 2 ( 3 y ^ 2 − 2 y ^ ) ( y = 0 ) ( 1 ) = − 2 y ^ ( 3 y ^ − 2 ) ( 2 ) ⇒ { y ^ ∈ [ 0 , 2 3 ] g ( y ^ ) ≥ 0 y ^ ∈ ( 2 3 , 1 ] g ( y ^ ) < 0 ( 3 ) \begin{array}{rlr} g(\hat{y}) & =-2\left(3 \hat{y}^{2}-2 \hat{y}\right) \quad (y=0) & (1)\\ & =-2 \hat{y}(3 \hat{y}-2) & (2)\\ & \Rightarrow\left\{\begin{aligned} \hat{y} \in\left[0, \frac{2}{3}\right] & g(\hat{y}) \geq 0 \\ \hat{y} \in\left(\frac{2}{3}, 1\right] & g(\hat{y})<0 \end{aligned}\right. & (3) \end{array} g(y^)=−2(3y^2−2y^)(y=0)=−2y^(3y^−2)⇒⎩⎪⎪⎪⎨⎪⎪⎪⎧y^∈[0,32]y^∈(32,1]g(y^)≥0g(y^)<0(1)(2)(3)
由于使用MSE作为代价函数的黑塞矩阵不能保证是半正定的,说明其代价函数不是一个凸函数。
梯度下降法的下降方向
先来看下一元的泰勒公式12 ,其中 o(…) 表示括号内式子的高阶无穷小,多元泰勒公式就是前面的一、二阶导数改写成雅可比矩阵和黑塞矩阵的形式:
f ( x ) = f ( a ) + f ′ ( a ) 1 ! ( x − a ) + f ( 2 ) ( a ) 2 ! ( x − a ) 2 + ⋯ + f ( n ) ( a ) n ! ( x − a ) n + o ( ( x − a ) n ) f(x)=f(a)+\frac{f^{\prime}(a)}{1 !}(x-a)+\frac{f^{(2)}(a)}{2 !}(x-a)^{2}+\cdots+\frac{f^{(n)}(a)}{n !}(x-a)^{n}+o\left((x-a)^{n}\right) f(x)=f(a)+1!f′(a)(x−a)+2!f(2)(a)(x−a)2+⋯+n!f(n)(a)(x−a)n+o((x−a)n)
我的目标是每次迭代后的代价函数值比上次都小:
Cost ( w n + 1 ) < Cost ( w n ) \operatorname{Cost}(w_{n+1}) \lt \operatorname{Cost}(w_{n}) Cost(wn+1)<Cost(wn)
将对数几率回归的代价函数用多元的一阶泰勒公式近似,雅可比矩阵为代价函数的梯度:
Cost ( w ) ≈ Cost ( A ) + ∇ Cost ( A ) T ( w − A ) \operatorname{Cost}(w) \approx \operatorname{Cost}(A)+\nabla \operatorname{Cost}(A)^{T}(w-A) Cost(w)≈Cost(A)+∇Cost(A)T(w−A)
(1)将 w n w_n wn 带入 A, w n + 1 w_{n+1} wn+1 带入 w
(2) w n + 1 − w n = Δ w w_{n+1} - w_n = Δw wn+1−wn=Δw,移项可以看到需要保证梯度乘 Δw 小于 0
(3)当 Δw 为负的梯度时,可以保证梯度乘 Δw 小于 0
(4)这样就得到了梯度下降的下降方向
Cost ( w n + 1 ) ≈ Cost ( w n ) + ∇ Cost ( w n ) T ( w n + 1 − w n ) ( 1 ) Cost ( w n + 1 ) − Cost ( w n ) ≈ ∇ Cost ( w n ) T Δ w < 0 ( 2 ) ∇ Cost ( w n ) T Δ w = − ∇ Cost ( w n ) T ∇ Cost ( w n ) < 0 ( 3 ) Δ w = − ∇ Cost ( w n ) ( 4 ) \begin{aligned} \operatorname{Cost}\left(w_{n+1}\right) & \approx \operatorname{Cost}\left(w_{n}\right)+\nabla \operatorname{Cost}\left(w_{n}\right)^{T}\left(w_{n+1}-w_{n}\right) & (1) \\ \operatorname{Cost}\left(w_{n+1}\right)-\operatorname{Cost}\left(w_{n}\right) & \approx \nabla \operatorname{Cost}\left(w_{n}\right)^{T} \Delta w<0 & (2) \\ \nabla \operatorname{Cost}\left(w_{n}\right)^{T} \Delta w &=-\nabla \operatorname{Cost}\left(w_{n}\right)^{T} \nabla \operatorname{Cost}\left(w_{n}\right)<0 & (3) \\ \Delta w &=-\nabla \operatorname{Cost}\left(w_{n}\right) & (4) \end{aligned} Cost(wn+1)Cost(wn+1)−Cost(wn)∇Cost(wn)TΔwΔw≈Cost(wn)+∇Cost(wn)T(wn+1−wn)≈∇Cost(wn)TΔw<0=−∇Cost(wn)T∇Cost(wn)<0=−∇Cost(wn)(1)(2)(3)(4)
牛顿法的下降方向
将对数几率回归的代价函数用多元的二阶泰勒公式近似,雅可比矩阵为代价函数的梯度,H 为代价函数的黑塞矩阵:
Cost ( w ) ≈ Cost ( A ) + ∇ Cost ( A ) T ( w − A ) + 1 2 ( w − A ) T H ( w − A ) \operatorname{Cost}(w) \approx \operatorname{Cost}(A)+\nabla \operatorname{Cost}(A)^{T}(w-A)+\frac{1}{2}(w-A)^{T} H(w-A) Cost(w)≈Cost(A)+∇Cost(A)T(w−A)+21(w−A)TH(w−A)
(1)将 w n w_n wn 带入 A,并对近似函数求梯度,另梯度等于 0 向量,这时取得当前的极小值
(2)这样就得到了牛顿法的下降方向
∇ Cost ( w ) = ∇ Cost ( w n ) + H ( w − w n ) = 0 ( 1 ) w = w n − H − 1 ∇ Cost ( w n ) ( 2 ) \begin{aligned} \nabla \operatorname{Cost}(w) &=\nabla \operatorname{Cost}\left(w_{n}\right)+H\left(w-w_{n}\right)=0 & (1) \\ w &=w_{n}-H^{-1} \nabla \operatorname{Cost}\left(w_{n}\right) & (2) \end{aligned} ∇Cost(w)w=∇Cost(wn)+H(w−wn)=0=wn−H−1∇Cost(wn)(1)(2)
五、代码实现
使用 Python 实现对数几率回归算法(梯度下降法):
import numpy as np
c_1 = 1e-4
c_2 = 0.9
def cost(X, y, w):
"""
对数几率回归的代价函数
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
return:
代价函数值
"""
power = -np.multiply(y, X.dot(w))
p1 = power[power <= 0]
p2 = -power[-power < 0]
# 解决 python 计算 e 的指数幂溢出的问题
return np.sum(np.log(1 + np.exp(p1))) + np.sum(np.log(1 + np.exp(p2)) - p2)
def dcost(X, y, W):
"""
对数几率回归的代价函数的梯度
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
return:
代价函数的梯度
"""
return X.T.dot(np.multiply(-y, 1 / (1 + np.exp(np.multiply(y, X.dot(w))))))
def direction(d):
"""
更新的方向
args:
d - 梯度
return:
更新的方向
"""
return -d
def sufficientDecrease(X, y, w, step):
"""
判断是否满足充分下降条件(sufficient decrease condition)
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
step - 步长
return:
是否满足充分下降条件
"""
d = dcost(X, y, w)
p = direction(d)
return cost(X, y, w + step * p) <= cost(X, y, w) + c_1 * step * p.T.dot(d)
def curvature(X, y, w, step):
"""
判断是否满足曲率条件(curvature condition)
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
step - 步长
return:
是否满足曲率条件
"""
d = dcost(X, y, w)
p = direction(d)
return -p.T.dot(dcost(X, y, w + step * p)) <= -c_2 * p.T.dot(d)
def select(step_low, step_high):
"""
在范围内选择一个步长,直接取中值
args:
step_low - 步长范围开始值
step_high - 步长范围结束值
return:
步长
"""
return (step_low + step_high) / 2
def lineSearch(X, y, w, step_init, step_max):
"""
线搜索步长,使其满足 Wolfe 条件
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
step_init - 步长初始值
step_max - 步长最大值
return:
步长
"""
step_i = step_init
step_low = step_init
step_high = step_max
i = 1
d = dcost(X, y, w)
p = direction(d)
while (True):
# 不满足充分下降条件或者后面的代价函数值大于前一个代价函数值
if (not sufficientDecrease(X, y, w, step_i) or (cost(X, y, w + step_i * p) >= cost(X, y, w + step_low * p) and i > 1)):
# 将当前步长作为搜索的右边界
# return search(X, y, w, step_prev, step_i)
step_high = step_i
else:
# 满足充分下降条件并且满足曲率条件,即已经满足了 Wolfe 条件
if (curvature(X, y, w, step_i)):
# 直接返回当前步长
return step_i
step_low = step_i
# 选择下一个步长
step_i = select(step_low, step_high)
i = i + 1
def logisticRegressionGd(X, y, max_iter=1000, tol=1e-4, step_init=0, step_max=10):
"""
对数几率回归,使用梯度下降法(gradient descent)
args:
X - 训练数据集
y - 目标标签值
max_iter - 最大迭代次数
tol - 变化量容忍值
step_init - 步长初始值
step_max - 步长最大值
return:
w - 权重系数
"""
# 初始化 w 为零向量
w = np.zeros(X.shape[1])
# 开始迭代
for it in range(max_iter):
# 计算梯度
d = dcost(X, y, w)
# 当梯度足够小时,结束迭代
if np.linalg.norm(x=d, ord=1) <= tol:
break
# 使用线搜索计算步长
step = lineSearch(X, y, w, step_init, step_max)
# 更新权重系数 w
w = w + step * direction(d)
return w
使用 Python 实现对数几率回归算法(牛顿法):
import numpy as np
c_1 = 1e-4
c_2 = 0.9
def cost(X, y, w):
"""
对数几率回归的代价函数
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
return:
代价函数值
"""
power = -np.multiply(y, X.dot(w))
p1 = power[power <= 0]
p2 = -power[-power < 0]
# 解决 python 计算 e 的指数幂溢出的问题
return np.sum(np.log(1 + np.exp(p1))) + np.sum(np.log(1 + np.exp(p2)) - p2)
def dcost(X, y, w):
"""
对数几率回归的代价函数的梯度
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
return:
代价函数的梯度
"""
return X.T.dot(np.multiply(-y, 1 / (1 + np.exp(np.multiply(y, X.dot(w))))))
def ddcost(X, y, w):
"""
对数几率回归的代价函数的黑塞矩阵
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
return:
代价函数的黑塞矩阵
"""
exp = np.exp(np.multiply(y, X.dot(w)))
result = np.multiply(exp, 1 / np.square(1 + exp))
X_r = np.zeros(X.shape)
for i in range(X.shape[1]):
X_r[:, i] = np.multiply(result, X[:, i])
return X_r.T.dot(X)
def direction(d, H):
"""
更新的方向
args:
d - 梯度
H - 黑塞矩阵
return:
更新的方向
"""
return - np.linalg.inv(H).dot(d)
def sufficientDecrease(X, y, w, step):
"""
判断是否满足充分下降条件(sufficient decrease condition)
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
step - 步长
return:
是否满足充分下降条件
"""
d = dcost(X, y, w)
H = ddcost(X, y, w)
p = direction(d, H)
return cost(X, y, w + step * p) <= cost(X, y, w) + c_1 * step * p.T.dot(d)
def curvature(X, y, w, step):
"""
判断是否满足曲率条件(curvature condition)
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
step - 步长
return:
是否满足曲率条件
"""
d = dcost(X, y, w)
H = ddcost(X, y, w)
p = direction(d, H)
return -p.T.dot(dcost(X, y, w + step * p)) <= -c_2 * p.T.dot(d)
def select(step_low, step_high):
"""
在范围内选择一个步长
args:
step_low - 步长范围开始值
step_high - 步长范围结束值
return:
步长
"""
return (step_low + step_high) / 2
def lineSearch(X, y, w, step_init, step_max):
"""
线搜索步长,使其满足 Wolfe 条件
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
step_init - 步长初始值
step_max - 步长最大值
return:
步长
"""
step_i = step_init
step_low = step_init
step_high = step_max
i = 1
d = dcost(X, y, w)
H = ddcost(X, y, w)
p = direction(d, H)
while (True):
# 不满足充分下降条件或者后面的代价函数值大于前一个代价函数值
if (not sufficientDecrease(X, y, w, step_i) or (cost(X, y, w + step_i * p) >= cost(X, y, w + step_low * p) and i > 1)):
# 将当前步长作为搜索的右边界
# return search(X, y, w, step_prev, step_i)
step_high = step_i
else:
# 满足充分下降条件并且满足曲率条件,即已经满足了 Wolfe 条件
if (curvature(X, y, w, step_i)):
# 直接返回当前步长
return step_i
step_low = step_i
# 选择下一个步长
step_i = select(step_low, step_high)
i = i + 1
def logisticRegressionNewton(X, y, max_iter=1000, tol=1e-4, step_init=0, step_max=10):
"""
对数几率回归,使用牛顿法(newton's method)
args:
X - 训练数据集
y - 目标标签值
max_iter - 最大迭代次数
tol - 变化量容忍值
step_init - 步长初始值
step_max - 步长最大值
return:
w - 权重系数
"""
# 初始化 w 为零向量
w = np.zeros(X.shape[1])
# 开始迭代
for it in range(max_iter):
# 计算梯度
d = dcost(X, y, w)
# 计算黑塞矩阵
H = ddcost(X, y, w)
# 当梯度足够小时,结束迭代
if np.linalg.norm(d) <= tol:
break
# 使用线搜索计算步长
step = lineSearch(X, y, w, step_init, step_max)
# 更新权重系数 w
w = w + step * direction(d, H)
return w
六、第三方库实现
scikit-learn13 实现无正则化的对数几率回归:
from sklearn.linear_model import LogisticRegression
# 初始化对数几率回归器,无正则化
reg = LogisticRegression(penalty="none")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_
scikit-learn13 实现L1正则化的对数几率回归:
from sklearn.linear_model import LogisticRegression
# 初始化对数几率回归器,L1正则化,使用坐标下降法
reg = LogisticRegression(penalty="l1", C=10, solver="liblinear")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_
scikit-learn13 实现L2正则化的对数几率回归:
from sklearn.linear_model import LogisticRegression
# 初始化对数几率回归器,L2正则化
reg = LogisticRegression(penalty="l2", C=10)
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_
scikit-learn13 实现弹性网络正则化的对数几率回归:
from sklearn.linear_model import LogisticRegression
# 初始化对数几率回归器,弹性网络正则化
reg = LogisticRegression(penalty="elasticnet", C=10, l1_ratio=0.5, solver="saga")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_
七、动画演示
下图展示了演示数据,其中红色表示标签值为1、蓝色表示标签值为-1:
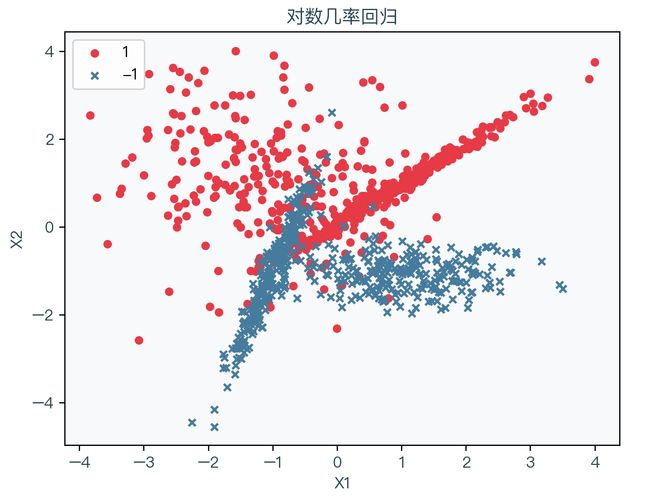
下图为使用梯度下降法拟合数据的结果,其中浅红色表示拟合后根据权重系数计算出预测值为1的部分,浅蓝色表示拟合后根据权重系数计算出预测值为-1的部分:
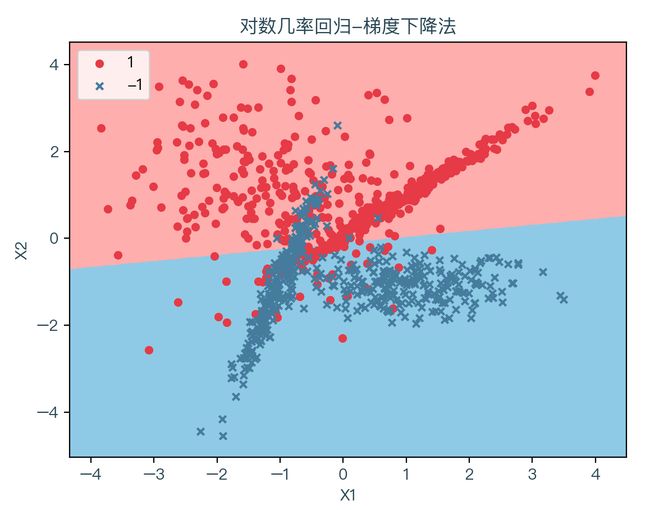
下图对比了不同的正则化方式对结果的影响,正则化惩罚项系数 C = 0.01,弹性网络中 ρ = 0.5。
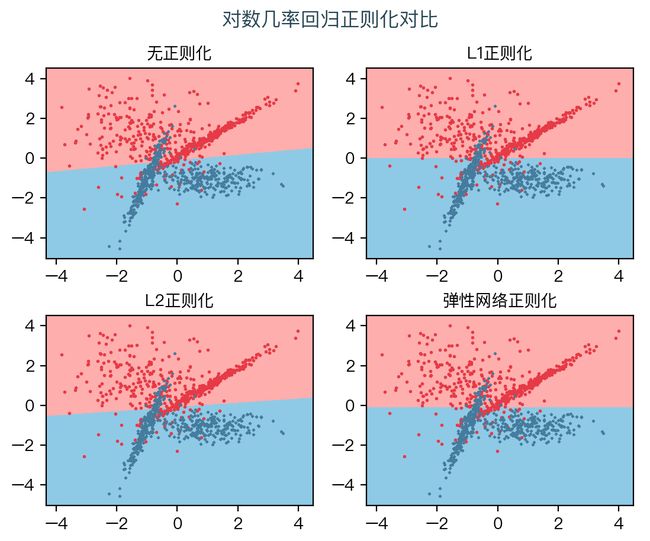
八、思维导图
九、参考文献
- https://en.wikipedia.org/wiki/Logistic_regression
- https://en.wikipedia.org/wiki/Sigmoid_function
- https://en.wikipedia.org/wiki/Logistic_function
- https://en.wikipedia.org/wiki/Mean_squared_error
- https://en.wikipedia.org/wiki/Likelihood_function
- https://en.wikipedia.org/wiki/Maximum_likelihood_estimation
- https://en.wikipedia.org/wiki/Gradient_descent
- https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
- https://en.wikipedia.org/wiki/Line_search
- https://en.wikipedia.org/wiki/Wolfe_conditions
- https://towardsdatascience.com/why-not-mse-as-a-loss-function-for-logistic-regression-589816b5e03c
- https://en.wikipedia.org/wiki/Taylor%27s_theorem
- https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注