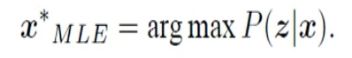VSLAM14T-6-非线性优化
目标:
- 理解最小二次法
- 理解高斯牛顿、levenburg-Marquadt下降测录俄
- 学习Ceres和g2o
问题给定观测方程和运动方程进行状态估计
情况:
- 最简单情况:线性系统、高斯噪声(卡尔曼解决)
- 复杂情况:非线性系统、非高斯噪声(分情况讨论)
之前我们都是用滤波器求解状态估计,单色需要满足马尔科夫性
现在非线性优化已经成为主流
状态估计问题
状态估计等同于求解条件分布P(x|z,u) 也就是已知运动数据和观测数据求解状态变量x
如果没有运动数据,只有观测数据,类似SfM Sturcture from Motion
即求P(x|z),但是这个条件分布很难求解,所以我们可以转换为
可以将最大似然估计转化为最小二乘问题
协方差矩阵里值越大越相关,逆里值越小越相关。 Qk,j ^-1是信息矩阵
Cartographer 中的协方差矩阵和信息矩阵
实践
root@asber-X550VX:/etc/apt/sources.list.d# sudo apt-get install libcxsparse3.1.2正在读取软件包列表... 完成
正在分析软件包的依赖关系树
正在读取状态信息... 完成
E: 无法定位软件包 libcxsparse3.1.2
E: 无法按照 glob ‘libcxsparse3.1.2’ 找到任何软件包
E: 无法按照正则表达式 libcxsparse3.1.2 找到任何软件包
https://blog.csdn.net/weixin_42744670/article/details/82797586
#include
#include
#include
#include
using namespace std;
// 代价函数的计算模型
struct CURVE_FITTING_COST
{
CURVE_FITTING_COST ( double x, double y ) : _x ( x ), _y ( y ) {}
// 残差的计算
template
bool operator() (
const T* const abc, // 模型参数,有3维
T* residual ) const // 残差
{
residual[0] = T ( _y ) - ceres::exp ( abc[0]*T ( _x ) *T ( _x ) + abc[1]*T ( _x ) + abc[2] ); // y-exp(ax^2+bx+c)
return true;
}
const double _x, _y; // x,y数据
};
int main ( int argc, char** argv )
{
double a=1.0, b=2.0, c=1.0; // 真实参数值
int N=100; // 数据点
double w_sigma=1.0; // 噪声Sigma值
cv::RNG rng; // OpenCV随机数产生器
double abc[3] = {0,0,0}; // abc参数的估计值
vector x_data, y_data; // 数据
cout<<"generating data: "< (
new CURVE_FITTING_COST ( x_data[i], y_data[i] )
),
nullptr, // 核函数,这里不使用,为空
abc // 待估计参数
);
}
// 配置求解器
ceres::Solver::Options options; // 这里有很多配置项可以填
options.linear_solver_type = ceres::DENSE_QR; // 增量方程如何求解
options.minimizer_progress_to_stdout = true; // 输出到cout
ceres::Solver::Summary summary; // 优化信息
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
ceres::Solve ( options, &problem, &summary ); // 开始优化
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration time_used = chrono::duration_cast>( t2-t1 );
cout<<"solve time cost = "< asber@asber-X550VX:~/slambook-master/slambook/ch6/ceres_curve_fitting/build$ ./curve_fitting
generating data:
0 2.71828
0.01 2.93161
0.02 2.12942
0.03 2.46037
0.04 4.18814
0.05 2.73368
0.06 2.42751
0.07 3.44729
0.08 3.72543
0.09 2.1358
0.1 4.12333
0.11 3.38199
0.12 4.81164
0.13 1.62582
0.14 1.76862
0.15 3.21555
0.16 3.0922
0.17 5.82752
0.18 4.29855
0.19 2.74081
0.2 5.75724
0.21 3.53729
0.22 1.95514
0.23 2.99195
0.24 3.28739
0.25 4.70749
0.26 6.24365
0.27 5.81645
0.28 4.88402
0.29 4.75991
0.3 7.25246
0.31 5.92933
0.32 7.00306
0.33 5.22286
0.34 5.16179
0.35 7.26191
0.36 6.40545
0.37 6.25549
0.38 6.56094
0.39 6.53523
0.4 8.14891
0.41 7.77616
0.42 7.40141
0.43 8.75638
0.44 7.20606
0.45 7.57795
0.46 8.21564
0.47 9.84032
0.48 6.96725
0.49 9.90619
0.5 9.27125
0.51 9.87567
0.52 10.3412
0.53 9.55315
0.54 11.3635
0.55 10.8815
0.56 13.0648
0.57 11.4756
0.58 11.337
0.59 13.2393
0.6 13.5299
0.61 14.0441
0.62 13.31
0.63 13.672
0.64 14.8504
0.65 14.2599
0.66 14.7724
0.67 17.4339
0.68 17.4632
0.69 17.7598
0.7 16.8223
0.71 19.9468
0.72 20.5446
0.73 21.3767
0.74 20.1435
0.75 20.3088
0.76 23.2543
0.77 23.4349
0.78 22.8706
0.79 24.094
0.8 25.4183
0.81 25.5237
0.82 27.9738
0.83 28.5861
0.84 29.5703
0.85 29.6744
0.86 32.667
0.87 34.2698
0.88 33.5124
0.89 36.1479
0.9 39.2485
0.91 40.988
0.92 41.5716
0.93 41.3686
0.94 44.285
0.95 42.8312
0.96 47.7941
0.97 48.5931
0.98 51.8487
0.99 51.0258
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.824887e+04 0.00e+00 1.38e+03 0.00e+00 0.00e+00 1.00e+04 0 2.41e-05 8.70e-05
1 2.748700e+39 -2.75e+39 0.00e+00 7.67e+01 -1.52e+35 5.00e+03 1 3.29e-05 2.03e-04
2 2.429783e+39 -2.43e+39 0.00e+00 7.62e+01 -1.35e+35 1.25e+03 1 1.69e-05 2.64e-04
3 1.213227e+39 -1.21e+39 0.00e+00 7.30e+01 -6.73e+34 1.56e+02 1 1.41e-05 3.19e-04
4 1.852387e+37 -1.85e+37 0.00e+00 5.56e+01 -1.03e+33 9.77e+00 1 1.29e-05 3.72e-04
5 6.714689e+31 -6.71e+31 0.00e+00 2.96e+01 -3.85e+27 3.05e-01 1 1.31e-05 4.25e-04
6 9.500531e+12 -9.50e+12 0.00e+00 9.50e+00 -8.39e+08 4.77e-03 1 1.31e-05 4.78e-04
7 1.776982e+04 4.79e+02 1.83e+03 2.58e-01 1.18e+00 1.43e-02 1 3.41e-05 5.50e-04
8 1.599969e+04 1.77e+03 3.45e+03 5.53e-01 1.46e+00 4.29e-02 1 2.88e-05 6.19e-04
9 1.060557e+04 5.39e+03 7.62e+03 7.33e-01 1.68e+00 1.29e-01 1 3.00e-05 6.89e-04
10 3.669783e+03 6.94e+03 9.60e+03 5.25e-01 1.39e+00 3.86e-01 1 2.91e-05 7.57e-04
11 5.397541e+02 3.13e+03 5.00e+03 2.66e-01 1.12e+00 1.16e+00 1 2.79e-05 8.24e-04
12 1.484444e+02 3.91e+02 1.22e+03 8.46e-02 1.02e+00 3.48e+00 1 2.79e-05 8.91e-04
13 1.216815e+02 2.68e+01 3.76e+02 4.17e-02 1.01e+00 1.04e+01 1 2.79e-05 9.58e-04
14 9.290109e+01 2.88e+01 2.42e+02 9.10e-02 1.01e+00 3.13e+01 1 2.81e-05 1.03e-03
15 6.674330e+01 2.62e+01 1.09e+02 1.33e-01 1.00e+00 9.39e+01 1 2.81e-05 1.09e-03
16 5.936574e+01 7.38e+00 2.14e+01 1.08e-01 9.94e-01 2.82e+02 1 2.81e-05 1.16e-03
17 5.653118e+01 2.83e+00 1.36e+01 1.57e-01 9.98e-01 8.45e+02 1 2.81e-05 1.23e-03
18 5.310764e+01 3.42e+00 8.50e+00 2.81e-01 9.89e-01 2.53e+03 1 2.81e-05 1.30e-03
19 5.125939e+01 1.85e+00 2.84e+00 2.98e-01 9.90e-01 7.60e+03 1 2.69e-05 1.36e-03
20 5.097693e+01 2.82e-01 4.34e-01 1.48e-01 9.95e-01 2.28e+04 1 2.81e-05 1.43e-03
21 5.096854e+01 8.39e-03 3.24e-02 2.87e-02 9.96e-01 6.84e+04 1 2.81e-05 1.50e-03
solve time cost = 0.00156354 seconds.
Ceres Solver Report: Iterations: 22, Initial cost: 1.824887e+04, Final cost: 5.096854e+01, Termination: CONVERGENCE
estimated a,b,c = 0.891943 2.17039 0.944142 #include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
// 曲线模型的顶点,模板参数:优化变量维度和数据类型
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
virtual void setToOriginImpl() // 重置
{
_estimate << 0,0,0;
}
virtual void oplusImpl( const double* update ) // 更新
{
_estimate += Eigen::Vector3d(update);
}
// 存盘和读盘:留空
virtual bool read( istream& in ) {}
virtual bool write( ostream& out ) const {}
};
// 误差模型 模板参数:观测值维度,类型,连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差
void computeError()
{
const CurveFittingVertex* v = static_cast (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
_error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
}
virtual bool read( istream& in ) {}
virtual bool write( ostream& out ) const {}
public:
double _x; // x 值, y 值为 _measurement
};
int main( int argc, char** argv )
{
double a=1.0, b=2.0, c=1.0; // 真实参数值
int N=100; // 数据点
double w_sigma=1.0; // 噪声Sigma值
cv::RNG rng; // OpenCV随机数产生器
double abc[3] = {0,0,0}; // abc参数的估计值
vector x_data, y_data; // 数据
cout<<"generating data: "< > Block; // 每个误差项优化变量维度为3,误差值维度为1
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense(); // 线性方程求解器
Block* solver_ptr = new Block( linearSolver ); // 矩阵块求解器
// 梯度下降方法,从GN, LM, DogLeg 中选
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm( solver ); // 设置求解器
optimizer.setVerbose( true ); // 打开调试输出
// 往图中增加顶点
CurveFittingVertex* v = new CurveFittingVertex();
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );
// 往图中增加边
for ( int i=0; isetId(i);
edge->setVertex( 0, v ); // 设置连接的顶点
edge->setMeasurement( y_data[i] ); // 观测数值
edge->setInformation( Eigen::Matrix::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆
optimizer.addEdge( edge );
}
// 执行优化
cout<<"start optimization"< time_used = chrono::duration_cast>( t2-t1 );
cout<<"solve time cost = "<estimate();
cout<<"estimated model: "< 于g2o新版本编译出错的原因及解决办法
Linux卸载用cmake安装第三方库
卸载cmake库
卸载之后install_manifest.txt还在而且还可以看到不如usr/local/include 下的文件,但是应该是删除了
找到源码的g20
Linux 下面解压.tar.gz 和.gz文件解压的方式
库虽然很多warmming但是还是装好了,make后运行发生如下错误
asber@asber-X550VX:~/slambook-master/slambook/ch6/g2o_curve_fitting/build$ ./curve_fitting
./curve_fitting: error while loading shared libraries: libg2o_core.so: cannot open shared object file: No such file or directory
根据https://www.cnblogs.com/lizhongping/p/7881368.html说的:
在默认情况下,编译器只会使用/lib和/usr/lib这两个目录下的库文件,通过源码包进行安装时,如果不指定--prefix会将库安装在/usr/local目录下,而又没有在文件/etc/ld.so.conf中添加 /usr/local/lib这个目录。这样虽然安装了源码包,但是使用时仍然找不到相关的.so库,就会报错。也就是说系统不知道安装了源码包。网络上的解决方法是在/etc/ld.so.conf里添加绝对路径/usr/local/lib.
在该文件中直接另起一行,直接写路径。/usr/local/lib
最后将修改写入缓存!!
sudo ldconfig
asber@asber-X550VX:~/slambook-master/slambook/ch6/g2o_curve_fitting/build$ sudo ldconfig /sbin/ldconfig.real: /usr/lib/ 不是符号链接 asber@asber-X550VX:~/slambook-master/slambook/ch6/g2o_curve_fitting/build$ cmake .. -- Configuring done -- Generating done -- Build files have been written to: /home/asber/slambook-master/slambook/ch6/g2o_curve_fitting/build asber@asber-X550VX:~/slambook-master/slambook/ch6/g2o_curve_fitting/build$ make -j2 [100%] Built target curve_fitting asber@asber-X550VX:~/slambook-master/slambook/ch6/g2o_curve_fitting/build$ ./curve_fitting generating data: 0 2.71828 0.01 2.93161 0.02 2.12942 0.03 2.46037 0.04 4.18814 0.05 2.73368 0.06 2.42751 0.07 3.44729 0.08 3.72543 0.09 2.1358 0.1 4.12333 0.11 3.38199 0.12 4.81164 0.13 1.62582 0.14 1.76862 0.15 3.21555 0.16 3.0922 0.17 5.82752 0.18 4.29855 0.19 2.74081 0.2 5.75724 0.21 3.53729 0.22 1.95514 0.23 2.99195 0.24 3.28739 0.25 4.70749 0.26 6.24365 0.27 5.81645 0.28 4.88402 0.29 4.75991 0.3 7.25246 0.31 5.92933 0.32 7.00306 0.33 5.22286 0.34 5.16179 0.35 7.26191 0.36 6.40545 0.37 6.25549 0.38 6.56094 0.39 6.53523 0.4 8.14891 0.41 7.77616 0.42 7.40141 0.43 8.75638 0.44 7.20606 0.45 7.57795 0.46 8.21564 0.47 9.84032 0.48 6.96725 0.49 9.90619 0.5 9.27125 0.51 9.87567 0.52 10.3412 0.53 9.55315 0.54 11.3635 0.55 10.8815 0.56 13.0648 0.57 11.4756 0.58 11.337 0.59 13.2393 0.6 13.5299 0.61 14.0441 0.62 13.31 0.63 13.672 0.64 14.8504 0.65 14.2599 0.66 14.7724 0.67 17.4339 0.68 17.4632 0.69 17.7598 0.7 16.8223 0.71 19.9468 0.72 20.5446 0.73 21.3767 0.74 20.1435 0.75 20.3088 0.76 23.2543 0.77 23.4349 0.78 22.8706 0.79 24.094 0.8 25.4183 0.81 25.5237 0.82 27.9738 0.83 28.5861 0.84 29.5703 0.85 29.6744 0.86 32.667 0.87 34.2698 0.88 33.5124 0.89 36.1479 0.9 39.2485 0.91 40.988 0.92 41.5716 0.93 41.3686 0.94 44.285 0.95 42.8312 0.96 47.7941 0.97 48.5931 0.98 51.8487 0.99 51.0258 start optimization iteration= 0 chi2= 30373.727656 time= 6.4364e-05 cumTime= 6.4364e-05 edges= 100 schur= 0 lambda= 699.050482 levenbergIter= 7 iteration= 1 chi2= 13336.948288 time= 4.1424e-05 cumTime= 0.000105788 edges= 100 schur= 0 lambda= 1864.134619 levenbergIter= 3 iteration= 2 chi2= 6946.262996 time= 3.5167e-05 cumTime= 0.000140955 edges= 100 schur= 0 lambda= 1242.756412 levenbergIter= 1 iteration= 3 chi2= 271.023166 time= 3.526e-05 cumTime= 0.000176215 edges= 100 schur= 0 lambda= 414.252137 levenbergIter= 1 iteration= 4 chi2= 118.903887 time= 3.5178e-05 cumTime= 0.000211393 edges= 100 schur= 0 lambda= 138.084046 levenbergIter= 1 iteration= 5 chi2= 113.568660 time= 3.5155e-05 cumTime= 0.000246548 edges= 100 schur= 0 lambda= 46.028015 levenbergIter= 1 iteration= 6 chi2= 107.476457 time= 3.5186e-05 cumTime= 0.000281734 edges= 100 schur= 0 lambda= 15.342672 levenbergIter= 1 iteration= 7 chi2= 103.014522 time= 3.5111e-05 cumTime= 0.000316845 edges= 100 schur= 0 lambda= 5.114224 levenbergIter= 1 iteration= 8 chi2= 101.988348 time= 3.5e-05 cumTime= 0.000351845 edges= 100 schur= 0 lambda= 1.704741 levenbergIter= 1 iteration= 9 chi2= 101.937388 time= 3.5012e-05 cumTime= 0.000386857 edges= 100 schur= 0 lambda= 0.568247 levenbergIter= 1 iteration= 10 chi2= 101.937021 time= 3.5308e-05 cumTime= 0.000422165 edges= 100 schur= 0 lambda= 0.378831 levenbergIter= 1 iteration= 11 chi2= 101.937020 time= 3.5076e-05 cumTime= 0.000457241 edges= 100 schur= 0 lambda= 0.252554 levenbergIter= 1 iteration= 12 chi2= 101.937020 time= 4.0653e-05 cumTime= 0.000497894 edges= 100 schur= 0 lambda= 1.346956 levenbergIter= 3 iteration= 13 chi2= 101.937020 time= 3.5092e-05 cumTime= 0.000532986 edges= 100 schur= 0 lambda= 0.897971 levenbergIter= 1 iteration= 14 chi2= 101.937020 time= 4.3433e-05 cumTime= 0.000576419 edges= 100 schur= 0 lambda= 38.313418 levenbergIter= 4 iteration= 15 chi2= 101.937020 time= 4.0713e-05 cumTime= 0.000617132 edges= 100 schur= 0 lambda= 204.338228 levenbergIter= 3 iteration= 16 chi2= 101.937020 time= 3.4921e-05 cumTime= 0.000652053 edges= 100 schur= 0 lambda= 136.225485 levenbergIter= 1 iteration= 17 chi2= 101.937020 time= 5.4646e-05 cumTime= 0.000706699 edges= 100 schur= 0 lambda= 24378500205.440712 levenbergIter= 8 iteration= 18 chi2= 101.937020 time= 4.0503e-05 cumTime= 0.000747202 edges= 100 schur= 0 lambda= 1560224013148.205566 levenbergIter= 3 solve time cost = 0.0012591 seconds. estimated model: 0.890912 2.1719 0.943629