一定把vslam拿下！！！-Ch2刚体运动（小白版）

一定把vslam拿下！！！（小白版）// 部分内容转载自他人博客！侵删

---

深蓝学院视觉十四讲课后作业——ch2 刚体运动
本文记录了学习的部分笔记心得与课后习题 主要用途为学习巩固、方便自己查阅
部分内容参阅互联网或者书籍知识，部分图片来自网络，欢迎批评指正
如有问题，可及时与我沟通讨论！

---

*熟悉 Eigen 矩阵运算 (2 分，约 2 小时)

Eigen（http://eigen.tuxfamily.org）是常用的 C++ 矩阵运算库，具有很高的运算效率。大部分
需要在 C++ 中使用矩阵运算的库，都会选用 Eigen 作为基本代数库，例如 Google Tensorflow，Google
Ceres，GTSAM 等。本次习题，你需要使用 Eigen 库，编写程序，求解一个线性方程组。为此，你需要先
了解一些有关线性方程组数值解法的原理。
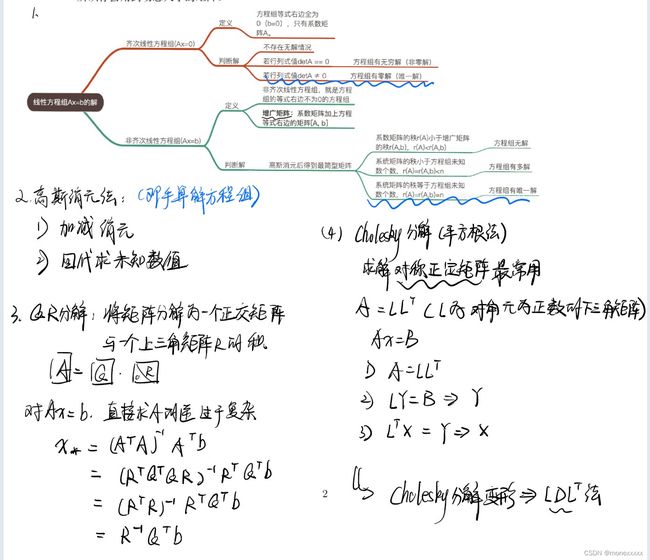
设线性方程 Ax = b，在 A 为方阵的前提下，请回答以下问题：

1. 在什么条件下，x 有解且唯一？

2. 高斯消元法的原理是什么？

3. QR 分解的原理是什么？

4. Cholesky 分解的原理是什么？
   

5. 编程实现 A 为 100 × 100 随机矩阵时，用 QR 和 Cholesky 分解求 x 的程序。你可以参考本次课
   用到的 useEigen 例程。
   代码如下：

#include 

#include 
// Eigen 部分
#include 
// 稠密矩阵的代数运算（逆，特征值等）
#include 

using namespace std;
using namespace Eigen;

#define MATRIX_SIZE 100

int main(int argc, char const *argv[])
{
    MatrixXd A;
    MatrixXd B;
    MatrixXd X1;
    MatrixXd X2;
    A = MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);
    B = MatrixXd::Random(MATRIX_SIZE,1);
    clock_t time_stt = clock(); //time_1

    //X = A.inverse() *B
    X1 = A.colPivHouseholderQr().solve(B);//QR
    cout<<"time use in QR decomposition is" << 1000*(clock()-time_stt)/(double)CLOCKS_PER_SEC<<"ms"<

运行结果：

可知 chelosky分解法的运算速度远快于 QR 分解法。

提示：你可能需要参考相关的数学书籍或文章。请善用搜索引擎。Eigen 固定大小矩阵最大支持到 50，
所以你会用到动态大小的矩阵。

矩阵论基础 （2 分，约 2 小时）

除了我们本科学过的基础线性代数之外，大部分研究生课程还会开设矩阵论课程，以作为对本科阶段
知识的扩充。对于很多线性问题（SLAM 里也会碰到许多线性问题），了解一些矩阵论基础知识是很有好
处的。我们在附件中为大家提供了张贤达老师的《矩阵分析与应用》。请参考该书内容（或者你能找到的其
他书籍），回答以下问题。

1. 什么是正定矩阵和半正定矩阵？
   正定和半正定这两个词的英文分别是positive definite和positive semi-definite。
   若所有特征值均大于零，则称为正定。
   若所有特征值均不小于零，则称为半正定。

2. 对于方阵 A，它的特征值是什么？特征向量是什么？特征值一定是实数吗？如何计算一个矩阵的
   特征值？
   (1) 只有方阵才存在特征值和特征向量；
   (2) 方阵的特征向量一定是非零向量；
   (3) 对于方阵A来说，对应于同一特征值的特征向量不唯一.
   
   
   特征值不一定是实数，也可能是虚数。
   如何计算矩阵的特征值：
   

3. 什么是矩阵的相似性？相似性反映了什么几何意义？
   

反映的几何意义：
相似的矩阵是同一个线性变换在不同基/坐标系下的的不同描述。线性变换若粗略看成一个刚体的特定运动。刚体的特定运动是同一个，但坐标系改变的话这个运动的描述函数就会不一样，如果这个函数可用矩阵等价替代的话，一个坐标系就对应着一个矩阵，因此这些矩阵就不同，但这些矩阵必有关系，这个关系就是相似。
（作者：renguangqian
链接：https://www.zhihu.com/question/25352258/answer/67426927
来源：知乎）

4. 矩阵一定能对角化吗？什么样的矩阵能保证对角化？不能对角化的矩阵能够形成什么样的形式（Jor-dan 标准形）？
   
   

来源：知乎

5. 奇异值分解（SVD）是什么意思？

6. 矩阵的伪逆是什么意思（Pseudo inverse）？莫尔——彭多斯逆是如何定义的？怎么计算一个矩阵的
伪逆？
伪逆矩阵是逆矩阵的广义形式。由于奇异矩阵或非方阵的矩阵不存在逆矩阵，但在matlab里可以用函数pinv(A)求其伪逆矩阵。基本语法为X=pinv(A),X=pinv(A,tolo),其中tolo为误差,pinv为pseudo-inverse的缩写。

（a）实际上，对于超定方程Ax = 0的解就是 ATA 最小特征值对应的特征向量。

简单的讲　所有的矩阵都可以进行奇异值分解，不管其是否是方阵以及对称矩阵。当所给的矩阵是对称的方阵，A(T)=A，二者的结果是相同的。也就是说对称矩阵的特征值分解是所有奇异值分解的一个特例。

但是二者还是存在一些小的差异，奇异值分解需要对奇异值从大到小的排序，而且全部是大于等于零。

特征值用来描述方阵，可看做是从一个空间到自身的映射，这也表现在了名字eigenvalue中。奇异值可以描述长方阵或奇异矩阵，可看做是从一个空间到另一个空间的映射。
————————————————
版权声明：本文为CSDN博主「啦啦啦1231213」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/m0_61238051/article/details/120606022

---

（b）对于超定方程Ax = 0的解就是 ATA 最小特征值对应的特征向量。
（c）可以通过近似将原来无解的问题，求出近似解。且在坐标系图中，每个样本点与拟合直线间的距离即代表估计的误差。

**

几何运算练习 (2 分，约 1 小时)

**
下面我们来练习如何使用 Eigen/Geometry 计算一个具体的例子。
一个机器人上通常会安装许多不同的传感器，而且这些传感器之间还存在固连关系。我们举一个典型
的例子。
在世界系 W 下，存在一个运动的机器人 R。按照固定的或者某些开发人员或者领导的特殊喜好，R
系定义在机器人脚部的位置。但是机器人在设计的时候，又定义了 B 系（Body 系，或本体系），位于机器
人头部的位置。由于沟通不畅，标定人员把一台激光传感器和一台视觉传感器标定在了 B 系下。我们称激
光传感器为 L 系，视觉传感器为 C 系。现在请你完成以下工作：

1. 说明一个激光传感器下的看到的点应该如何计算它的世界坐标。
2. 取：qW R = [0.55, 0.3, 0.2, 0.2], tW R = [0.1, 0.2, 0.3]T，qRB = [0.99, 0, 0, 0.01], tRB = [0.05, 0, 0.5]T，
   qBL = [0.3, 0.5, 0, 20.1], tBL = [0.4, 0, 0.5]T
   , qBC = [0.8, 0.2, 0.1, 0.1], tBC = [0.5, 0.1, 0.5]T。现在假
   设相机传感器观察到自身坐标系下的点 [0.3, 0.2, 1.2]，请计算：
   (a)这个点在激光系下的坐标；
   (b)这个点在世界系下的坐标。
   提示：
3. 本题的数据是随意取的，没有真实意义，产生什么结果都不要奇怪。
4. 四元数在使用前需要归一化。
5. 请注意 Eigen 在使用四元数时的虚部和实部顺序。

 
using namespace std;
 
#include 
#include 
 
using namespace Eigen;
 
int main(int argc, char ** argv){
 
    //创建视觉传感器和激光传感器的四元数
    Quaterniond q_BL(0.3, 0.5, 0,20.1), q_BC(0.8, 0.2, 0.1, 0.1);
    //四元数归一化
    q_BC.normalize();
    q_BL.normalize();
 
    //平移向量t1和t2
    Vector3d t_BL(0.4, 0, 0.5), t_BC(0.5, 0.1, 0.5);
    //p1坐标
    Vector3d p1(0.3, 0.2, 1.2);
 
    //变换矩阵Tc1w和Tc2w
    Isometry3d T_BL(q_BL), T_BC(q_BC);
    T_BL.pretranslate(t_BL);
    T_BC.pretranslate(t_BC);
 
    //计算p2
    Vector3d p2 = T_BL.inverse()*T_BC*p1;
    cout <<"这个点在视觉传感器系下的坐标"<< p2.transpose() << endl;
       Vector3d p23= T_BL*T_BC.inverse()*p1;
    cout <<"这个点在激光系下的坐标"<< p23.transpose() << endl;
 
  //创建世界系和机器人本体的四元数
    Quaterniond q3(0.55, 0.3, 0.2,0.2), q4(0.99, 0, 0, 0.01);
    //四元数归一化
    q3.normalize();
    q4.normalize();
 
    //平移向量t3和t4
    Vector3d t3(0.1, 0.2, 0.3), t4(0.05, 0, 0.5);
 
 
    //变换矩阵Tc3w和Tc4w
    Isometry3d Tc3w(q3), Tc4w(q4);
    Tc3w.pretranslate(t3);
    Tc4w.pretranslate(t4);
 
    //计算p3
    Vector3d p3 = Tc4w*Tc3w*p1;
    cout <<"这个点在世界系下的坐标"<< p3.transpose() << endl;
 
 
    return 0;
    }

**

旋转的表达 （2 分，约 1 小时）

**
课程中提到了旋转可以用旋转矩阵、旋转向量与四元数表达，其中旋转矩阵与四元数是日常应用中常
见的表达方式。请根据课件知识，完成下述内容的证明。

罗德里格斯公式的证明 (1 分，约 1 小时)

  ***从其他网页摘录推导如下：***（前面的部分分解没有很看懂....）

至此，得证。
转自 https://www.cnblogs.com/jingrui/p/9712461.html

四元数运算性质的验证 (1 分，约 1 小时)

不行了 今天看不下去矩阵… 改日再战

熟悉 C++11 (2 分，约 1 小时)

C++ 是一门古老的语言，但它的标准至今仍在不断发展。在 2011 年、2014 年和 2017 年，C++ 的标
准又进行了更新，被称为 C++11，C++14，C++17。其中，C++11 标准是最重要的一次更新，让 C++
发生了重要的改变，也使得近年来的 C++ 程序与你在课本上（比如谭浩强）学到的 C++ 程序有很大的
不同。你甚至会惊叹这是一种全新的语言。C++14 和 C++17 则是对 11 标准的完善与扩充。
越来越多的程序开始使用 11 标准，它也会让你在写程序时更加得心应手。本题中，你将学习一些 11
标准下的新语法。请参考本次作业 books/目录下的两个 pdf，并回答下面的问题。
设有类 A，并有 A 类的一组对象，组成了一个 vector。现在希望对这个 vector 进行排序，但排序的
方式由 A.index 成员大小定义。那么，在 C++11 的语法下，程序写成：

1. 序列for循环

for循环 可以用于遍历数组，容器，string以及由begin和end函数定义的序列（即有Iterator）。

2. 新的关键字auto（新东西！）

C++11中引入auto第一种作用是为了自动类型推导
auto的自动类型推导，用于从初始化表达式中推断出变量的数据类型。通过auto的自动类型推导，可以大大简化我们的编程工作，auto实际上实在编译时对变量进行了类型推导，所以不会对程序的运行效率造成不良影响。另外，似乎auto并不会影响编译速度，因为编译时本来也要右侧推导然后判断与左侧是否匹配。

3. Lambda表达式（新东西捏！）

lambda表达式类似Javascript中的闭包，它可以用于创建并定义匿名的函数对象，以简化编程工作。
Lambda的语法如下：
[函数对象参数]（操作符重载函数参数）->返回值类型{函数体}

————————————————
版权声明：本文为CSDN博主「小白的进修之路」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_44218240/article/details/105765486

**

ch3算是草草的完结惹 ^ ^ 还剩一点点数学推导

**