机器学习之决策树01

最近学习了唐宇迪老师关于决策树算法视频，感觉看了老师的视频，再结合李航老师《统计学习方法》书上的内容，还是能够有所理解的。

一，决策树

       可以将决策树看成一个 if-then 规则的集合。理论上来说，只要数据的特征足够，那么这课决策树可以无限地伸展下去，你可以将树的结点的每一次判断看成“切一刀”，没切一刀，就能将数据分得更准确。（当然，现实生活中并没有提供这么多的特征，并且如果分得太开，那么过拟合的可能性就会提高——在训练集上准确率很高，测试集很差）

二，决策树的训练与测试
训练阶段：从给定的训练集构造出来一棵树（从跟节点开始选择特征，如何进行特征切分）
测试阶段：根据构造出来的树模型从上到下去走一遍就好了

        一旦构造好了决策树，那么分类或者预测任务就很简单了，只需要走一遍就可以了，那么难点就在于如何构造出来一颗树，这就没那么容易了，需要考虑的问题还有很多的！

三，决策树的特征选择（即选择树的结点）

3.1 衡量标准-熵 

        熵：熵是表示随机变量不确定性的度量（解释：说白了就是物体内部的混乱程度，比如杂货市场里面什么都有那肯定混乱呀，专卖店里面只卖一个牌子的那就稳定多啦）
公式：H(X)= - ∑ pi * logpi, i=1,2, ... , n

        例如：A集合[1,1,1,1,1,1,1,1,2,2]    B集合[1,2,3,4,5,6,7,8,9,1]
显然A集合的熵值要低，因为A里面只有两种类别，相对稳定一些而B中类别太多了，熵值就会大很多。（在分类任务中我们希望通过节点分支后数据类别的熵值大还是小呢？） 

熵：不确定性越大，得到的熵值也就越大
当p=0或p=1时，H(p)=0,随机变量完全没有不确定性
当p=0.5时，H(p)=1,此时随机变量的不确定性最大 

                    

3.2 结点的选择

决策树一般是通过信息增益来选择结点的。

信息增益：表示特征X使得类Y的不确定性减少的程度。（分类后的专一性，希望分类后的结果是同类在一起）

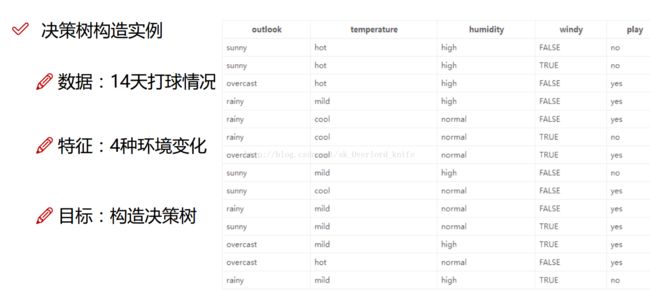
例如：我们根据已知的数据，去判断，某人在天气，温度，湿度，是否有风这几个因素确定的情况下，他是否去打球。

在这里，我们知道了，是否去打球，这是我们判断的结果，我们把它称为“属性”；而，影响的因素——天气等，称之为“特征”。

我们要做的是，根据已知的数据，通过不断地划分特征，从而构造决策树，明白某人在什么情况组合下回去打球，什么情况下，不去。

当然，由于数据有限（且特征也有限），我们无法测试出这个人去打球的所有情况（那，只要列一个表格，就可以知道了，但现实情况下是不可能的），我们要做的就是让决策树更有可能地去预测，这时候，我们需要去衡量特征的重要性，什么样的特征很重要，在满足这个特征下，更能去预测（让数据更趋向有序）。比如，下雨天，那他不去打球的可能性就越大，那“下雨天”这个特征，会让数据更有序，熵更小，更能判断。

所以，我感觉衡量熵的过程，也是在比较特征重要性的过程，越重要的特征越能反应数据的趋势，越能使数据有序。

 在上面的例子中，我们可以选择四种划分方式（天气，湿度，温度，是否有风），那我们选择哪一种方式来划分呢？

首先，我们来看，不划分的时候的熵：

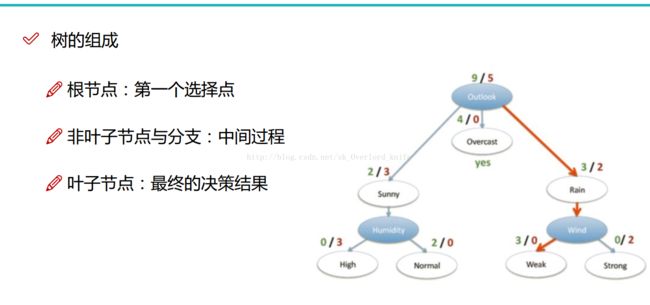
在历史数据中（14天）有9天打球，5天不打球，所以此时的熵应为：

- 9/14*log(9/14)-5/14*log(5/14)=0.940

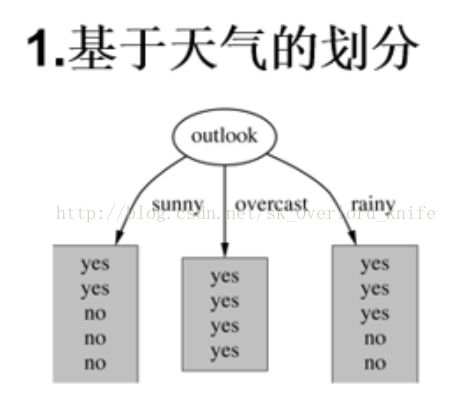
当我们按照天气来划分时：

                             

      第一组划分(sunny)熵值:   -2/5*log(2/5)-3/5*log(3/5)=  0.9710

      第二组划分(overcast)熵值: -4/4*log(4/)=0

      第三组划分(rainy)熵值:   -3/5*log(3/5)-2/5*log(2/5)=  0.9710

      根据数据统计，outlook取值分别为sunny,overcast,rainy的概率分别为：5/14, 4/14, 5/14
这里将三组熵合起来，使用李航书上的经验条件熵公式：5/14*  0.9710+4/14*0+5/14*0.9710=0.693

   从而，我们可以得到，按照第一个特征进行划分时的信息增益：系统的熵值从原始的0.940下降到了0.693，增益为0.247

同样的方式可以计算出其他特征的信息增益，那么我们选择最大的那个就可以啦，相当于是遍历了一遍特征，找出来了大当家（最重要的那个），然后按照最重要的那个特征划分结点。同一操作，划分每一组数据，直至数据中的特征使用完，如果最终的数据里面，存在属性不同的数据（例如，划分数据中，有去打球的，有不去打球的），那么我们一般按照多数原则，即数据中打球的多，那么，判定时，这个叶子节点就代表这人去打球。

四，决策树算法的进阶

ID3决策树就是上面提到的决策树

C4.5决策树在原来的基础上考虑自身的熵。即，使用信息增益作为划分依据时，划分时，存在偏向于选择取值较多的特征的问题。通过与原来的熵值的比值来划分，则可以有效校正这个问题。

CART决策树则是对熵这个判断依据做了改动，将熵改成了基尼系数。

五，决策树的剪枝

在李航老师的书上，着重讲解了后剪枝策略，在唐宇迪老师的视频上表示，在现实数据处理中，预剪枝策略更加实用。

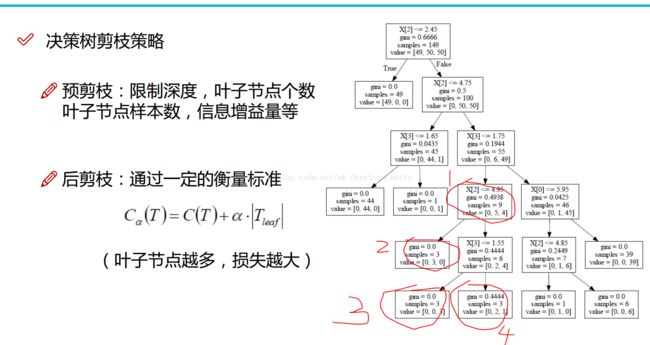
当时，看李航老师的后剪枝的时候，看证明看得头大（数学基础差），一直看不明白，在唐宇迪老师视频中，我直观的理解了上面这个公式，简单的来说，

如果，我们判断上图我画出来的  1  这个节点是否需要被剪枝（这里使用的gini系数来算的,samples代表这里面的数据个数）。

 首先，我们看，1如果被剪枝， C(T)=gini*9+a*1=0.4938*9 + a  （1代表一个自身，剪枝后，它变成一个叶子节点）

如果 1 被保留，  C(T)=0.0*3  +  0.0*3  + 0.4444*3 +  3*a   (分别为2,3,4，三个叶子节点的基尼系数与个数乘积  与 3*a 的和）

在这里，当上面的式子比下面的大，那么，说明被剪枝损失得大，所以我们不要剪枝；反之，如果小，则我们要对1进行剪枝。

在这里，a是对 训练数据的拟合程度与模型复杂度的一个衡量。（a越小，则表明对叶子节点的个数越不重视，即越可能不断分裂树节点，模型越复杂）

六，代码（sklearn实现）

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.externals.six import StringIO
import pydotplus
from IPython.display import Image
from sklearn.datasets.california_housing import fetch_california_housing
from sklearn import tree
from IPython.display import Image
#只考虑8个属性中的经度和纬度对房价的影响

housing=fetch_california_housing()
#print(housing)
#print(housing.data.shape)
#print(housing.data[0])



#实例化树模型
dtr=tree.DecisionTreeRegressor(max_depth=2)
dtr.fit(housing.data[:,[6,7]],housing.target)

#可视化过程
#安装 graphviz     http://www.graphviz.org/Download.php
#pip install pydotplus
dot_data = StringIO()
tree.export_graphviz(dtr, out_file=dot_data,
                        feature_names= housing.feature_names[6:8],
                        class_names=housing.target,
                        filled=True, rounded=True,
                        special_characters=True)

graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.get_nodes()[7].set_fillcolor("#FFF2DD")
graph.write_pdf("tree.pdf")
graph.write_png("tr.png")




#验证准确率
from sklearn.cross_validation import train_test_split
data_train,data_test,target_train,target_test=train_test_split(housing.data,
                                    housing.target,test_size=0.1,random_state=42)
dtr=tree.DecisionTreeRegressor(random_state=42)
dtr.fit(data_train,target_train)
print("准确率为："+str(dtr.score(data_test,target_test)))



#随机森林
from sklearn.ensemble import RandomForestRegressor
# rfr = RandomForestRegressor( random_state = 42)
# rfr.fit(data_train, target_train)
# rfr.score(data_test, target_test)

#sklearn中参数组合的模块
from sklearn.grid_search import GridSearchCV
tree_param_grid = { 'min_samples_split': list((3,6,9)),'n_estimators':list((10,50,100))}
grid = GridSearchCV(RandomForestRegressor(),param_grid=tree_param_grid, cv=5)
grid.fit(data_train, target_train)
print(grid.grid_scores_, grid.best_params_, grid.best_score_)



'''
树模型参数:
1.criterion gini or entropy
2.splitter best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中（数据量大的时候）
3.max_features None（所有），log2，sqrt，N 特征小于50的时候一般使用所有的
4.max_depth 数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下
5.min_samples_split 如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
6.min_samples_leaf 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝，如果样本量不大，不需要管这个值，大些如10W可是尝试下5
7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
8.max_leaf_nodes 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制具体的值可以通过交叉验证得到。
9.class_weight 指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用“balanced”，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。
10.min_impurity_split 这个值限制了决策树的增长，如果某节点的不纯度(基尼系数，信息增益，均方差，绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。
n_estimators:要建立树的个数
'''

七，感谢

感谢李航老师的《统计学习方法》

感谢唐宇迪老师的视频

感谢ApacheCN 开源组织对Sklearn 的中文翻译（群号:629470233）

感谢《机器学习实战》这本书对决策树的讲解（ApacheCN 开源组织也录制了该书的讲解视频）