RepVGG:极简架构,SOTA性能,让VGG式模型再次伟大
![]()
1.摘要
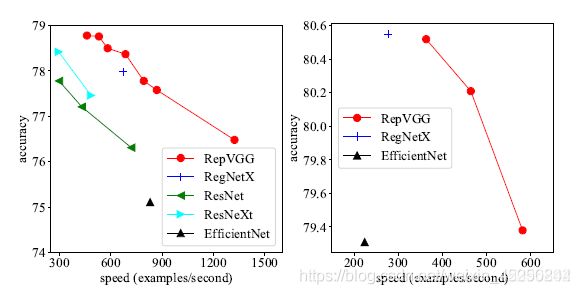
本文提出了一个简单但功能强大的卷积神经网络架构,该架构推理时候具有类似于VGG的骨干结构,该主体仅由3 x 3卷积和ReLU堆叠组成,而训练时候模型采用多分支拓扑结构。 训练和推理架构的这种解耦是通过结构重参数化技术实现的,因此该模型称为RepVGG。 在ImageNet上,据我们所知,RepVGG的top-1准确性达到80%以上,这是老模型首次实现该精度。 在NVIDIA 1080Ti GPU上,RepVGG模型的运行速度比ResNet-50快83%,比ResNet-101快101%,并且具有更高的精度,与诸如EfficientNet和RegNet的最新模型相比,RepVGG显示出良好的精度-速度权衡。 效果如下图:
2. 背景
现有最新的ConvNet通过复杂的结构设计都比简单的ConvNet提供更高的准确性,但缺点很明显:
-
多分支结构:第一次出现多分支结构应该是在Inception中(如果不是,请各位指正),就获得了高性能收益,加上不同分支应用不同卷积核,能获得不同感受野,后续出现的ResNet,其残差结构也是多路结构。但是需要注意的是:多路结构需要保存中间结果,显存占有量会明显增高,只有到多路融合时,显存会会降低。
-
性能优异组件:随着不断尝试于探索,出现了很多性能优异的网络组件,比如深度可分离卷积,分组卷积等等,这些都可以显著增加网络性能,但是,我们也知道,就拿group conv来说,当group越多是,我们知道网络性能会越好,但是,其MAC(内存访问成本)也会显著增大,最终导致模型变慢,深度可分离卷积虽然可以显著降低FLOPs,但是其MAC也会增加,最终导致模型速度变慢。
这就引发了一个矛盾,既然多分支结构和性能优异的组件能显著提高模型性能,但是,又会最终导致模型在推理时速度变慢且还非常耗内存,这非常不利于工业场景(尤其实在算力受限的情况下)。这种问题该怎么解决呢?repVGG给了我们答案:结构重参数化思想,也即训练时尽量用多分支结构来提升网络性能,而推理时,采用利用结构重参数化思想,将其变为单路结构,这样,显存占用少,推理速度又快。
作者最终选择将VGG作为backbone,这里为什么要选择这么古董的玩意儿呢,而不是选择现在主流的ResNet架构?主要是基于以下三点考虑:
-
速度快
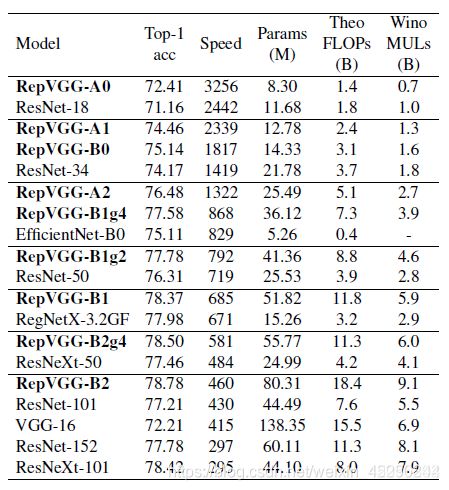
除了Winograd conv带来的加速之外,FLOPs和速度之间的差异可以归因于两个重要因素,它们对速度有很大影响,但FLOPs并未考虑这些因素:内存访问成本(MAC)和并行度。 另一方面,在相同的FLOPs下,具有高并行度的模型可能比具有低并行度的模型快得多。因此简单的推理结构可以避免多分支的零碎计算。我们都知道,VGG几乎都是由3x3卷积堆叠而成,而现在加速库比如NVIDIA的cudNN,Intel的MKL和相关硬件对3x3的卷积核有非常好的性能优化,而在VGG中,几乎都是conv3x3。因此,利用现有加速库,会得到更好的性能优化,从下表就就可以看出,在相同channels、input_size和batchsize条件下,不同卷积核的FLOPs和TFLOPs和用时,可以看出,3x3卷积非常快。在GPU上,3x3卷积的计算密度(理论运算量(Theoretical FLOPs ÷ Time usage)除以所用时间)可达1x1和5x5卷积的4倍。

-
节省内存
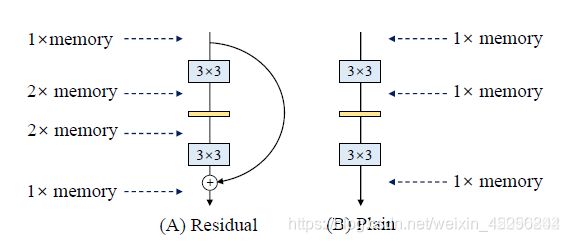
如上图所示,多分支拓扑结构由于需要保留每个分支的结果,直到相加或串联为止,从而显着提高了内存占用的峰值。 假设该块保持特征图的大小,则内存占用的峰值为2倍。 相反,简单的拓扑允许在操作完成后立即释放特定层的输入所占用的内存。
VGG是一个直筒性单路结构,由上述分析可知,单路结构会占有更少的内存,因为不需要保存其中间结果,同时,单路架构非常快,因为并行度高。同样的计算量,大而整的运算效率远超小而碎的运算。 -
灵活性好
多分支结构会引入网络结构的约束,比如Resnet的残差结构要求输入和卷积出来的张量维度要一致(这样才能相加),这种约束导致网络不易延伸拓展,也一定程度限制了通道剪枝。对应的单路结构就比较友好,非常容易改变各层的宽度,这样剪枝后也能得到很好的加速比。
RepVGG主体部分只有一种算子: conv3x3+ReLU。在设计专用芯片时,给定芯片尺寸或造价,我们可以集成海量的3x3卷积-ReLU计算单元来达到很高的效率。别忘了,单路架构省内存的特性也可以帮我们少做存储单元。
综上所述,我们提出regVGG结构,如下图所示:
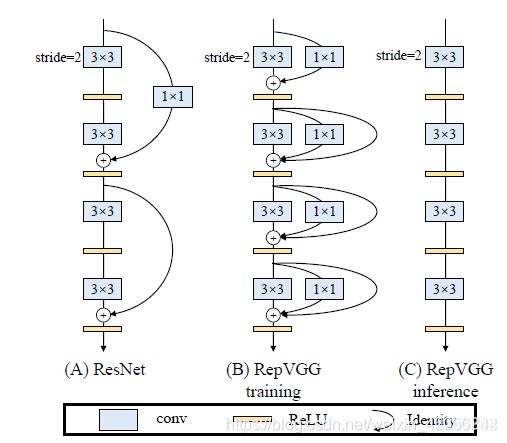
可以看到,我们在原始VGG基础上,引入和残差分支和1x1卷积分支,为了后续重参数化成单路结构,我们调整了分支放置的位置,没有进行跨层连接,而是直接连了过去,后续的对比试验也证明了残差分支和conv_1x1均能增加网络性能,如下图所示:

3. 网络训练
训练时采用的多分支结构采用3 x 3卷积 + 1 x 1卷积 + identity分支,比较简单,这里不再赘述。直接看代码:需要注意的是:1.通过deploy设置来进行重参数化推理;2.identity分支并不是直接相加,是有BN的
class RepVGGBlock(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size,
stride=1, padding=0, dilation=1, groups=1, padding_mode='zeros', deploy=False):
super(RepVGGBlock, self).__init__()
self.deploy = deploy
self.groups = groups
self.in_channels = in_channels
assert kernel_size == 3
assert padding == 1
padding_11 = padding - kernel_size // 2
self.nonlinearity = nn.ReLU()
#用过deploy设置进行重参数化
if deploy:
self.rbr_reparam = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=stride,
padding=padding, dilation=dilation, groups=groups, bias=True, padding_mode=padding_mode)
else:
self.rbr_identity = nn.BatchNorm2d(num_features=in_channels) if out_channels == in_channels and stride == 1 else None
self.rbr_dense = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=stride, padding=padding, groups=groups)
self.rbr_1x1 = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=1, stride=stride, padding=padding_11, groups=groups)
print('RepVGG Block, identity = ', self.rbr_identity)
def forward(self, inputs):
if hasattr(self, 'rbr_reparam'):
return self.nonlinearity(self.rbr_reparam(inputs))
if self.rbr_identity is None:
id_out = 0
else:
id_out = self.rbr_identity(inputs)
return self.nonlinearity(self.rbr_dense(inputs) + self.rbr_1x1(inputs) + id_out)
4. 网络部署
网络在训练完毕后,怎样将多路模型转化为单路模型,最终部署到终端,这应该是本文的核心,如下图所示:
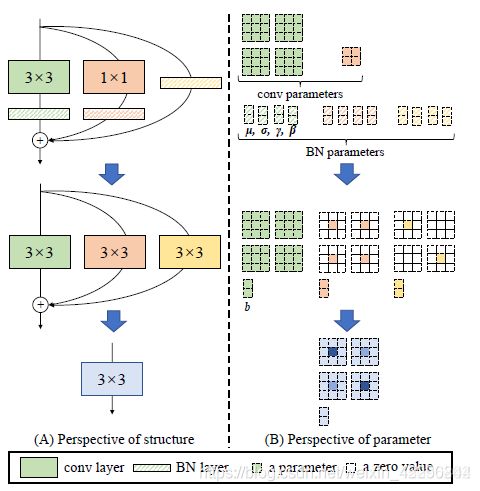
上述过程就是将训练好的multi_path model 转换为single_path model,从而最终在推理时达到高性能。上面训练过程用到的模型涉及到三路:常规的conv_3x3,conv_1x1,identity,且这三路每一路都跟着BN层,下面仔细讲解这三路是怎样合并成一个conv_3x3单元的。
4.1 卷积层和BN层合并
repVGG中大量运用conv+BN层,我们知道将层合并,减少层数能提升网络性能,下面的推理是conv带有bias的过程:

相关融合代码如下所示:
def _fuse_bn_tensor(self, branch):
if branch is None:
return 0, 0
if isinstance(branch, nn.Sequential):
kernel = branch.conv.weight
running_mean = branch.bn.running_mean
running_var = branch.bn.running_var
gamma = branch.bn.weight
beta = branch.bn.bias
eps = branch.bn.eps
else:
...
std = (running_var + eps).sqrt()
t = (gamma / std).reshape(-1, 1, 1, 1)
return kernel * t, beta - running_mean * gamma / std
4.2 conv_3x3和conv_1x1合并
这里为了详细说明下,假设输入特征图特征图尺寸为(1, 2, 3, 3),输出特征图尺寸与输入特征图尺寸相同,且stride=1,下面展示是conv_3x3的卷及过程:
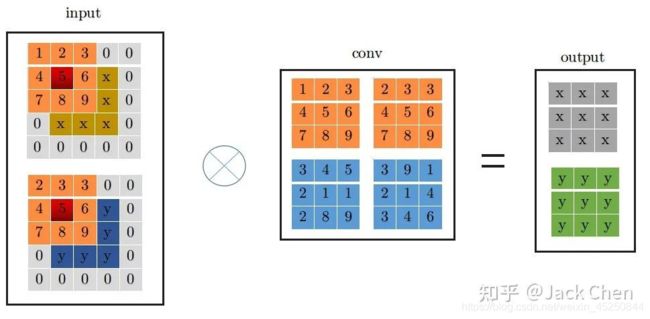
conv_3x3卷积过程大家都很熟悉,看上图一目了然,首先将特征图进行pad=kernel_size//2,然后从左上角开始(上图中红色位置)做卷积运算,最终得到右边output输出。下面是conv_1x1卷积过程:
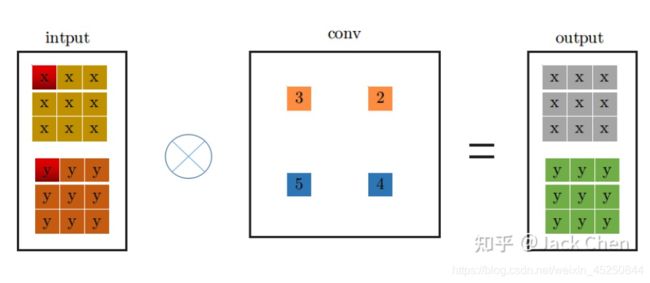
同理,conv_1x1跟conv_3x3卷积过程一样,从上图中左边input中红色位置开始进行卷积,得到右边的输出,观察conv_1x1和conv_3x3的卷积过程,可以发现他们都是从input中红色起点位置开始,走过相同的路径,因此,将conv_3x3和conv_1x1进行融合,只需要将conv_1x1卷积核padding成conv_3x3的形式,然后于conv_3x3相加,再与特征图做卷积(这里依据卷积的可加性原理)即可,也就是conv_1x1的卷积过程变成如下形式:
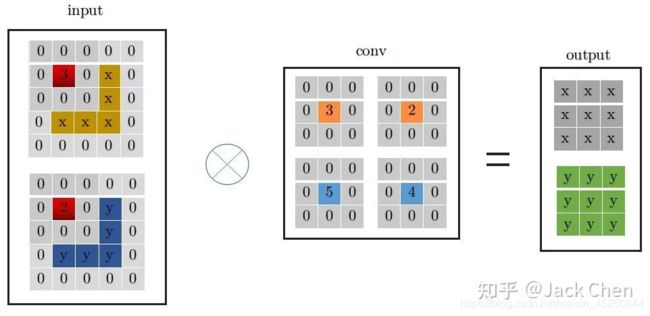
4.3 identity 等效为特殊权重的卷积层
identity层就是输入直接等于输出,也即input中每个通道每个元素直接输出到output中对应的通道,用一个什么样的卷积层来等效这个操作呢,我们知道,卷积操作必须涉及要将每个通道加起来然后输出的,然后又要保证input中的每个通道每个元素等于output中,从这一点,我们可以从PWconv想到,只要令当前通道的卷积核参数为1,其余的卷积核参数为0,就可以做到;从DWconv中可以想到,用conv_1x1卷积且卷积核权重为1,就能保证每次卷积不改变输入,因此,identity可以等效成如下的conv_1x1的卷积形式:
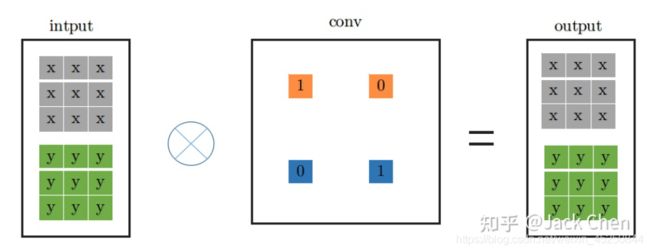
从上面的分析,我们进一步可以将indentity -> conv_1x1 -> conv_3x3的形式,如下所示:

上述过程就是对应论文中所属的下述从step1到step2的变换过程,涉及conv于BN层融合,conv_1x1与identity转化为等价的conv_3x3的形式:

结构重参数化的最后一步也就是上图中step2 -> step3, 这一步就是利用卷积可加性原理,将三个分支的卷积层和bias对应相加组成最终一个conv_3x3的形式即可。
5. 实验
5.1 Imagenet
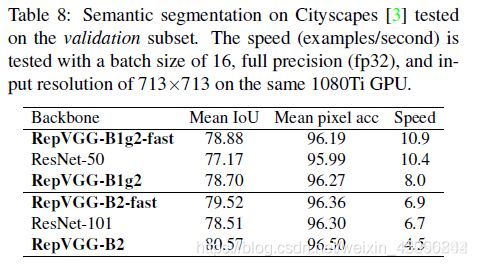
5.2 Semantic Segmentation
6. 最后
![]()