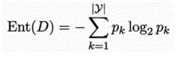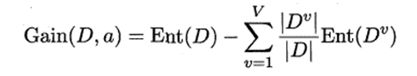机器学习 决策树ID3算法 连续值处理
文章目录
- 1. 开发环境
- 2.1 决策树算法
- 3.1 信息熵
-
- 3.2 信息增益
- 一、过程
-
- 1. 计算信息熵
- 2. 对连续值进行处理
- 3. 选择最优的属性划分
- 4. 按照列的属性值划分数据子集
- 4. 根据`pandas.DataFrame类型`建立决策树
- 5. 完整代码
- 二、读取Excel表格的数据
-
- 二、一 Excel表格数据
-
-
- 1. 西瓜数据集
- 2. 自定义数据集
-
- 三、绘制 PNG 图片的代码
-
- 1. 代码
- 1. 生成的PNG图片
- 2. 参考西瓜书数据集
- 四、测试生成树
-
- 1. 对测试集中的连续值进行离散化处理
- 2. 递归寻找匹配
- 3. 对生成树进行预测
1. 开发环境
- Python3.8
- Pandas1.0.3
- numpy 1.18.2
import pandas as pd
from math import log2
import numpy
2.1 决策树算法
3.1 信息熵
- 香农提出了“信息熵”的概念,解决了对信息的量化度量问题。香农用“信息熵”的概念来描述信源的不确定性
- “信息熵”是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为pk (k = 1, 2,. . . , |y|) ,则D的信息熵定义为
-
Ent(D)的值越小,则D的纯度越高。对于二分类任务,|y| = 2。
-
假设我们已经知道衡量不确定性大小的这个量已经存在了,不妨就叫做“信息量”
- 不会是负数
- 不确定性函数f是概率p的单调递减函数
- 可加性:两个独立符号所产生的不确定性应等于各自不确定性之和,即
- 一个事件的信息量就是这个事件发生的概率的负对数。信息熵是跟所有事件的可能性有关的,是平均而言发生一个事件得到的信息量大小。所以信息熵其实是信息量的期望
3.2 信息增益
- 假定离散属性a有V个可能的取值{a1, a2, …, av},若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D中所有在属性a上取值为av的样本,记为Dv。我们可根据公式计算出Dv的信息熵,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重| Dv |/|D|,即样本数越多的分支结点的影响越大,于是可计算出用属性a对样本集D进行划分所获得的“信息增益”
- 一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大。决策树算法第8行选择属性
一、过程
1. 计算信息熵
# 计算信息熵
def calculate_entropy(data: "DateFrame格式") -> "返回浮点数 entropy":
"""
计算公式 entropy = -pi * log2(pi) i为分类的个数
1. 获取非分类属性的属性值以及个数
2. 按照计算公式计算信息熵
:return: entropy(float)
"""
# 获取列
columns_items = data[data.columns[-1]]
# 获取取值以及取值的个数
labels = {}
for item, cnt in columns_items.value_counts().items(): # items 返回(value, count), 值, 个数
labels[item] = cnt
# 所有数据的行数
rows_count = len(columns_items)
# 计算信息熵
entropy = 0
for key in labels:
p = labels[key] / rows_count
entropy -= p * log2(p)
return entropy
pass
2. 对连续值进行处理
# 处理连续值得信息增益划分
def settle_continuous_data(data: "DateFrame数据,不对连续值处理") -> "返回保存连续值属性以及最优划分得字典":
"""
处理过程
1. 首先对每一列进行处理,规定连续值得数据类型是 int, float类型
2. 保存每一列得名字到列表, 方便对后面得方便对后面得表头进行修改
3. 对数值列进行处理, 取出这一列得数值,取 两两中值 对每一个中值进行信息增益的计算, 信息增益最大的
· 则是最优的连续值属性划分
4.处理细节
对每一个中间值进行信息增益的求解
:param data: DataFrame类型的数据
:return: 返回处理的data, 最优的连续值属性划分添加到表头
"""
# 连续值字典保存
continuous_number_dict = {}
# 按照列进行遍历
cols_count = len(data.columns)
# 保存列的名字进行设置
cols_names = list(data.columns)
for i in range(cols_count - 1): # 去掉最后一列类属性
if isinstance(data.iloc[0, i], (numpy.int64, numpy.float64)): # 如果取值是数值类型,则按照连续值进行处理
col_data = list(data.iloc[:, i]) # 取出连续值列, 使用集合进行去重操作
col_data.sort() # 从小到达的顺序进行排序
col_len = len(col_data)
print("col_data:", col_data)
# 计算中间值,保存到average
average = []
for j in range(col_len - 1):
average.append((col_data[j] + col_data[j + 1]) / 2)
# 最优的连续值
best_feature = 0
# 最优信息增益
best_info_gain = 0.0
# 未进行属性划分时的信息熵
base_entropy = calculate_entropy(data)
print("average: ", average)
# 对每一个中间值进行处理
for num in average:
# 中间值属性划分的信息熵
feature_entropy = 0.0
# 深拷贝一个该数据集, 对新的数据集的连续值,按照中间值,划分为 "大", "小", 原数据集还需要多次使用
new_data = data.copy(deep=True)
for j in range(len(data.iloc[:, i])):
if data.iloc[j, i] >= num:
new_data.iloc[j, i] = ">=" + str(num)
else:
new_data.iloc[j, i] = "<" + str(num)
# 2. 计算中间值划分后新数据集得信息增益
# 取连续值得列属性名
name_feature = new_data.columns[i]
# 属性得取值进行去重, 为了按照属性进行子数据集的划分
unique_value = set(new_data[name_feature])
# 按照每一个属性值划分子集, 计算信息增益
for value in unique_value:
sub_data = split_data(new_data, name_feature, value)
rate = len(sub_data) / len(new_data)
feature_entropy += rate * calculate_entropy(sub_data)
info_gain = base_entropy - feature_entropy
# 保存最优的中间值为属性值
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = num
# 显示最优的连续属性值划分
print("连续值处理: best_info_gain: ", info_gain)
print("连续值处理: Best feature ", best_feature)
# # 保存属性列的名称
# cols_names[i] = best_feature
# 保存属性到字典
continuous_number_dict[cols_names[i]] = best_feature
print("保存到字典的属性: ", continuous_number_dict)
# 返回连续值矩阵
return continuous_number_dict
pass
3. 选择最优的属性划分
# 选择最优的属性进行划分
def choose_best_feature_to_split(data: "原始的DataFrame数据集") -> "返回":
"""
选择最优的属性
1. 对连续值进行处理, 深拷贝一个数据集,对深拷贝的数据集,按照连续属性的最优划分(表头), 将属性划分为"大" 或 "小"
2. 对每一列计算其信息熵和信息增益, 选择最大的信息增益的属性作为最优的属性划分
:param new_data: 已经进行最优连续值划分的数据集
:return: 返回最优的属性名, 用于决策树的建立
"""
# 1. 首先对连续值进行处理
# 深拷贝一个数组
# 获取连续值
continuous_number_dict = settle_continuous_data(data)
# 深拷贝, 不破坏连续值
copy_data = data.copy(deep=True)
data_columns = list(copy_data.columns)
# 保存连续值的列表
num_feature_list = []
# 连续值的列保存到列表中
for item in continuous_number_dict.keys():
num_feature_list.append(item)
# 对每一个连续值列, 修改属性的取值为">" 或 "<"
for name in num_feature_list:
for i in range(len(copy_data)):
# 防止去掉属性后,因为Pandas.loc[i, name] name没有该列出错
if name in data_columns:
if copy_data.loc[i, name] >= continuous_number_dict[name]:
copy_data.loc[i, name] = ">=" + str(continuous_number_dict[name])
else:
copy_data.loc[i, name] = "<" + str(continuous_number_dict[name])
# 显示处理后的数据集
print("最优属性选择后的数据集: ", copy_data)
# 2. 对连续属性值处理后的数据集进行最优属性选择
# 取出数据集列
name_feature = copy_data.columns
# 计算未进行属性划分时数据集的信息熵
base_entropy = calculate_entropy(copy_data)
# 初始化 信息增益 和 最优划分属性
best_info_gain = 0.0
best_feature = 0
# 对数据集的每一列进行处理
for feature in name_feature[0:-1]:
unique_value = set(copy_data[feature]) # 取出去重后的属性取值
# 每一个属性的信息熵初始化
feature_entropy = 0.0
# 对每一个属性进行属性划分, 计算其信息增益
for value in unique_value:
sub_data = split_data(copy_data, feature, value)
rate = len(sub_data) / len(copy_data)
feature_entropy += rate * calculate_entropy(sub_data)
info_gain = base_entropy - feature_entropy
# 显示信息增益
print("最优属性划分: 信息增益: column: ", feature, " 信息增益: ", info_gain)
# 保存最优的属性划分
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = feature
# 显示最优的属性划分
print("最优属性划分: 最优属: ", best_feature)
return best_feature
pass
4. 按照列的属性值划分数据子集
# 划分数据集
def split_data(data: "DateFrame类型, 按照连续值划分", feature: "列名", feature_value: "列属性的取值") -> "按照属性的某个取值划分后的子集":
"""
根据信息 featrure属性 和 属性的取值 划分数据集
:param data: 类型 DataFrame
:param feature: DataFrame表的列头
:param feature_value: 每一列属性的取值
:return: 返回 属性列 feature 按照固定属性值 feature_value 的数据子集
去掉分类时的属性
"""
sub_data = []
n = len(data)
# 遍历数据的每一行
for i in range(n):
if data.iloc[[i], :][feature].values[0] == feature_value:
temp = data.loc[i] # 取改行数据
sub_data.append(list(temp))
sub_data_p = pd.DataFrame(sub_data, columns=list(data.columns))
# 去掉已经被划分的属性
del sub_data_p[feature]
return sub_data_p
4. 根据pandas.DataFrame类型建立决策树
# 建立决策树
def create_tree(data: "原始DateFrame数据集") -> "返回构造的Dict字典树":
"""
建立决策树
1. 递归结束的条件:
1). 只有类属性列,且类属性列的取值唯一, 取唯一的属性
2). 只有类属性列,类属性的取值不唯一,取概率较大的类为该类的划分
2. 对最优属性的连续值进行处理, 大于最优连续值取值为为 "大" 其余 取值为小
2. 取最优的属性值,按照其属性的分类,划分子树,子树为字典取值,建立决策树
:param data: 原始的数据集,未经过连续值得处理
:return: 返回字典, 字典的键为 属性 值为属性或者划分类
"""
# 1. 只有类属性时
# 取去掉分类的列, 分类是最后一列
data_columns = data.columns
columns_value = data[data_columns[-1]]
# 结束递归条件 只有一个类是结束划分
if len(columns_value.values) == columns_value.value_counts()[0]:
# print("len(columns_value.values): ", len(columns_value.values))
# print("columns_value.value_counts()[0]: ", columns_value.value_counts()[0])
# print("columns_value.values: ", columns_value.values)
# print("columns_value.value_counts(): ", columns_value.value_counts())
print("类的取值唯一,递归结束")
return columns_value.values[0]
# 递归结束的条件 只有一个属性的时候, 取分类数目较多的属性
if len(data_columns) == 1:
print("只有类那一列,类的取值不同")
class_dict = {}
# 取类取值最多的那一列
for item, value in columns_value.value_counts().items():
class_dict[item] = value
# 排序取最大
class_name = max(class_dict, key=lambda k: class_dict[k])
return class_name
# 2. 非只有类属性时
# 选择最优的属性划分
best_feature = choose_best_feature_to_split(data)
# 获取连续值
continuous_number_dict = settle_continuous_data(data)
if best_feature in continuous_number_dict.keys():
for i in range(len(data)):
if data.loc[i, best_feature] >= continuous_number_dict[best_feature]:
data.loc[i, best_feature] = ">=" + str(continuous_number_dict[best_feature])
else:
data.loc[i, best_feature] = "<" + str(continuous_number_dict[best_feature])
# 建立字典树,类型为{属性名: {分类 / 分支}}
tree = {best_feature: {}}
# 取最优属性列的值,递归划分数据集
unique_value = set(data[best_feature])
# 遍历每一个属性进行划分
for value in unique_value:
tree[best_feature][value] = create_tree(split_data(data, best_feature, value))
return tree
pass
5. 完整代码
# 决策树生成算法
import pandas as pd
from math import log2
import numpy
import treePlotter
def read_excel_df(url: "绝对路径") -> "DataFrame类型":
"""
:param url: url需要使用绝对路径, 相对路径会报错
:return: 返回Pandas.DataFrame类型数据
"""
return pd.read_excel(url)
pass
# 计算信息熵
def calculate_entropy(data: "DateFrame格式") -> "返回浮点数 entropy":
"""
计算公式 entropy = -pi * log2(pi) i为分类的个数
1. 获取非分类属性的属性值以及个数
2. 按照计算公式计算信息熵
:return: entropy(float)
"""
# 获取列
columns_items = data[data.columns[-1]]
# 获取取值以及取值的个数
labels = {}
for item, cnt in columns_items.value_counts().items(): # items 返回(value, count), 值, 个数
labels[item] = cnt
# 所有数据的行数
rows_count = len(columns_items)
# 计算信息熵
entropy = 0
for key in labels:
p = labels[key] / rows_count
entropy -= p * log2(p)
return entropy
pass
# 划分数据集
def split_data(data: "DateFrame类型, 按照连续值划分", feature: "列名", feature_value: "列属性的取值") -> "按照属性的某个取值划分后的子集":
"""
根据信息 featrure属性 和 属性的取值 划分数据集
:param data: 类型 DataFrame
:param feature: DataFrame表的列头
:param feature_value: 每一列属性的取值
:return: 返回 属性列 feature 按照固定属性值 feature_value 的数据子集
去掉分类时的属性
"""
sub_data = []
n = len(data)
# 遍历数据的每一行
for i in range(n):
if data.iloc[[i], :][feature].values[0] == feature_value:
temp = data.loc[i] # 取改行数据
sub_data.append(list(temp))
sub_data_p = pd.DataFrame(sub_data, columns=list(data.columns))
# 去掉已经被划分的属性
del sub_data_p[feature]
return sub_data_p
# 处理连续值得信息增益划分
def settle_continuous_data(data: "DateFrame数据,不对连续值处理") -> "返回保存连续值属性以及最优划分得字典":
"""
处理过程
1. 首先对每一列进行处理,规定连续值得数据类型是 int, float类型
2. 保存每一列得名字到列表, 方便对后面得方便对后面得表头进行修改
3. 对数值列进行处理, 取出这一列得数值,取 两两中值 对每一个中值进行信息增益的计算, 信息增益最大的
· 则是最优的连续值属性划分
4.处理细节
对每一个中间值进行信息增益的求解
:param data: DataFrame类型的数据
:return: 返回处理的data, 最优的连续值属性划分添加到表头
"""
# 连续值字典保存
continuous_number_dict = {}
# 按照列进行遍历
cols_count = len(data.columns)
# 保存列的名字进行设置
cols_names = list(data.columns)
for i in range(cols_count - 1): # 去掉最后一列类属性
if isinstance(data.iloc[0, i], (numpy.int64, numpy.float64)): # 如果取值是数值类型,则按照连续值进行处理
col_data = list(data.iloc[:, i]) # 取出连续值列, 使用集合进行去重操作
col_data.sort() # 从小到达的顺序进行排序
col_len = len(col_data)
print("col_data:", col_data)
# 计算中间值,保存到average
average = []
for j in range(col_len - 1):
average.append((col_data[j] + col_data[j + 1]) / 2)
# 最优的连续值
best_feature = 0
# 最优信息增益
best_info_gain = 0.0
# 未进行属性划分时的信息熵
base_entropy = calculate_entropy(data)
print("average: ", average)
# 对每一个中间值进行处理
for num in average:
# 中间值属性划分的信息熵
feature_entropy = 0.0
# 深拷贝一个该数据集, 对新的数据集的连续值,按照中间值,划分为 "大", "小", 原数据集还需要多次使用
new_data = data.copy(deep=True)
for j in range(len(data.iloc[:, i])):
if data.iloc[j, i] >= num:
new_data.iloc[j, i] = ">=" + str(num)
else:
new_data.iloc[j, i] = "<" + str(num)
# 2. 计算中间值划分后新数据集得信息增益
# 取连续值得列属性名
name_feature = new_data.columns[i]
# 属性得取值进行去重, 为了按照属性进行子数据集的划分
unique_value = set(new_data[name_feature])
# 按照每一个属性值划分子集, 计算信息增益
for value in unique_value:
sub_data = split_data(new_data, name_feature, value)
rate = len(sub_data) / len(new_data)
feature_entropy += rate * calculate_entropy(sub_data)
info_gain = base_entropy - feature_entropy
# 保存最优的中间值为属性值
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = num
# 显示最优的连续属性值划分
# print("连续值处理: best_info_gain: ", info_gain)
# print("连续值处理: Best feature ", best_feature)
# # 保存属性列的名称
# cols_names[i] = best_feature
# 保存属性到字典
continuous_number_dict[cols_names[i]] = best_feature
print("保存到字典的属性: ", continuous_number_dict)
# 返回连续值矩阵
return continuous_number_dict
pass
# 选择最优的属性进行划分
def choose_best_feature_to_split(data: "原始的DataFrame数据集") -> "返回":
"""
选择最优的属性
1. 对连续值进行处理, 深拷贝一个数据集,对深拷贝的数据集,按照连续属性的最优划分(表头), 将属性划分为"大" 或 "小"
2. 对每一列计算其信息熵和信息增益, 选择最大的信息增益的属性作为最优的属性划分
:param new_data: 已经进行最优连续值划分的数据集
:return: 返回最优的属性名, 用于决策树的建立
"""
# 1. 首先对连续值进行处理
# 深拷贝一个数组
# 获取连续值
continuous_number_dict = settle_continuous_data(data)
# 深拷贝, 不破坏连续值
copy_data = data.copy(deep=True)
data_columns = list(copy_data.columns)
# 保存连续值的列表
num_feature_list = []
# 连续值的列保存到列表中
for item in continuous_number_dict.keys():
num_feature_list.append(item)
# 对每一个连续值列, 修改属性的取值为">" 或 "<"
for name in num_feature_list:
for i in range(len(copy_data)):
# 防止去掉属性后,因为Pandas.loc[i, name] name没有该列出错
if name in data_columns:
if copy_data.loc[i, name] >= continuous_number_dict[name]:
copy_data.loc[i, name] = ">=" + str(continuous_number_dict[name])
else:
copy_data.loc[i, name] = "<" + str(continuous_number_dict[name])
# 显示处理后的数据集
# print("最优属性选择后的数据集: ", copy_data)
# 2. 对连续属性值处理后的数据集进行最优属性选择
# 取出数据集列
name_feature = copy_data.columns
# 计算未进行属性划分时数据集的信息熵
base_entropy = calculate_entropy(copy_data)
# 初始化 信息增益 和 最优划分属性
best_info_gain = 0.0
best_feature = 0
# 对数据集的每一列进行处理
for feature in name_feature[0:-1]:
unique_value = set(copy_data[feature]) # 取出去重后的属性取值
# 每一个属性的信息熵初始化
feature_entropy = 0.0
# 对每一个属性进行属性划分, 计算其信息增益
for value in unique_value:
sub_data = split_data(copy_data, feature, value)
rate = len(sub_data) / len(copy_data)
feature_entropy += rate * calculate_entropy(sub_data)
info_gain = base_entropy - feature_entropy
# 显示信息增益
print("最优属性划分: 信息增益: column: ", feature, " 信息增益: ", info_gain)
# 保存最优的属性划分
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = feature
# 显示最优的属性划分
print("最优属性划分: 最优属: ", best_feature)
return best_feature
pass
# 建立决策树
def create_tree(data: "原始DateFrame数据集") -> "返回构造的Dict字典树":
"""
建立决策树
1. 递归结束的条件:
1). 只有类属性列,且类属性列的取值唯一, 取唯一的属性
2). 只有类属性列,类属性的取值不唯一,取概率较大的类为该类的划分
2. 对最优属性的连续值进行处理, 大于最优连续值取值为为 "大" 其余 取值为小
2. 取最优的属性值,按照其属性的分类,划分子树,子树为字典取值,建立决策树
:param data: 原始的数据集,未经过连续值得处理
:return: 返回字典, 字典的键为 属性 值为属性或者划分类
"""
# 1. 只有类属性时
# 取去掉分类的列, 分类是最后一列
data_columns = data.columns
columns_value = data[data_columns[-1]]
# 结束递归条件 只有一个类是结束划分
if len(columns_value.values) == columns_value.value_counts()[0]:
# print("len(columns_value.values): ", len(columns_value.values))
# print("columns_value.value_counts()[0]: ", columns_value.value_counts()[0])
# print("columns_value.values: ", columns_value.values)
# print("columns_value.value_counts(): ", columns_value.value_counts())
print("类的取值唯一,递归结束")
return columns_value.values[0]
# 递归结束的条件 只有一个属性的时候, 取分类数目较多的属性
if len(data_columns) == 1:
print("只有类那一列,类的取值不同")
class_dict = {}
# 取类取值最多的那一列
for item, value in columns_value.value_counts().items():
class_dict[item] = value
# 排序取最大
class_name = max(class_dict, key=lambda k: class_dict[k])
return class_name
# 2. 非只有类属性时
# 选择最优的属性划分
best_feature = choose_best_feature_to_split(data)
# 获取连续值
continuous_number_dict = settle_continuous_data(data)
if best_feature in continuous_number_dict.keys():
for i in range(len(data)):
if data.loc[i, best_feature] >= continuous_number_dict[best_feature]:
data.loc[i, best_feature] = ">=" + str(continuous_number_dict[best_feature])
else:
data.loc[i, best_feature] = "<" + str(continuous_number_dict[best_feature])
# 建立字典树,类型为{属性名: {分类 / 分支}}
tree = {best_feature: {}}
# 取最优属性列的值,递归划分数据集
unique_value = set(data[best_feature])
# 遍历每一个属性进行划分
for value in unique_value:
tree[best_feature][value] = create_tree(split_data(data, best_feature, value))
return tree
pass
# 测试集中的数据离散化处理
def discrete_data(decision_tree: "建立的生成树", dict_test: "测试例子字典") -> "返回离散化处理后数据集":
"""
对测试集中的连续值进行离散化处理
1. 对于生成树, 第一层字典的值是属性列, 第二层是属性的取值
2. 取出第一层属性作为属性列, 取出第二层的属性作为属性的取值
3. 对测试集进行处理, 取出其中取值是数字(即连续性值)的属性列
4. 如果连续值得属性列 是 这个子树的第一层键(根节点), 比较第二层属性列, 进行连续值离散化处理
1). 大于属性值, 取>=0.2222
2). 小于属性值, 取 <0.222
5. 递归对下一层字典进行处理
:param decision_tree:
:param dict_test:
:return:
"""
# 如果字典树的 属性列 取值不为None
if decision_tree.keys() is not None:
# 取根节点的列属性
root_column = list(decision_tree.keys())[0]
# 取字典值字典的序
second_dict = decision_tree[root_column]
# 取第二层字典键,即是属性的取值
decision_value = list(second_dict.keys())
consecutive_column = []
for key in dict_test.keys():
if isinstance(dict_test[key], (int, float)):
consecutive_column.append(key)
# 对连续进行处理
for conlumn_value in consecutive_column:
# 取测试集的key 与 跟节点的属性进行比较
if root_column == conlumn_value:
for value in decision_value:
# 对测试集字典中的熟悉离散化处理
if value[0: 2] == ">=":
edit_value = value.replace("=", "")
else:
edit_value = value
if isinstance(dict_test[root_column], float):
# 测试集的属性 >= 最佳连续值的时候, 修改测试集中的连续值为: ">=最优连续值"
if float(edit_value[1:]) <= float(dict_test[root_column]):
dict_test[root_column] = ">=" + str(float(edit_value[1:]))
# 测试集的属性 < 最佳连续值的时候, 修改测试集中的连续值为: "<最优连续值"
elif float(str(edit_value)[1:]) > dict_test[root_column]:
dict_test[root_column] = "<" + str(float(edit_value[1:]))
for key in second_dict.keys():
# 第二层字典的取值仍是字典, 需要递归子树处理
if isinstance(second_dict[key], dict):
discrete_data(second_dict[key], dict_test)
return dict_test
pass
# 分类器预测
def match_class(decision_tree: "建立的生成树", dict_test: "测试的数据集") -> "返回判断后的类别":
"""
根据生成的决策时进行预测
1. 对于生成树, 第一层是属性列的值, 第二层是属性的取值
2. 对于测试字典, 第一层是属性列, 第二层是属性列的取值
3. 取生成树第一层属性列, 和第二层属性的取值, 属性值于测试集中对应列进行比较
1). 相等的时候, 判断属性的下一层的值是不是字典, 如果是字典, 则递归子树, 将值保存到class_label中作为结果
2). 下一层不是字典, 而是取值的时候, 赋值到class_label
4. 返回结果集为class_label
:param decision_tree: 建立的决策树
:param dict_test: : 测试集字典
:return: 返回生成树的分类
"""
root_column = list(decision_tree.keys())[0]
second_dict = decision_tree[root_column] # 获取字典树的取值, 第二个字典即属性取值
for key in second_dict.keys():
if key == dict_test[root_column]:
if type(second_dict[key]).__name__ == "dict": # 继续递归
class_label = match_class(second_dict[key], dict_test)
else:
class_label = second_dict[key]
return class_label
pass
# 对生成树进行预测
def predict(decision_tree: "建立的决策树", dict_test: "测试集的字典类型") -> "返回是 好瓜 或者 坏瓜":
discrete_dict_test = discrete_data(decision_tree, dict_test)
predict_result = match_class(decision_tree, discrete_dict_test)
return "好瓜" if predict_result == "Yes" else "坏瓜"
pass
if __name__ == "__main__":
# 作业数据集
url_1 = r"作业数据集.xlsx"
url_2 = r"作业数据集English.xlsx"
# 西瓜数据集
url_3 = r"西瓜数据集.xlsx"
url_4 = r"西瓜数据集English.xlsx"
# 建立生成树
data = read_excel_df(url_3) # 读取数据
decision_tree = create_tree(data) # 根据DataFrame数据建立字典树
print("建立的决策树字典: ", decision_tree) # 显示建立的字典树
# 绘制生成树
# treePlotter.createPlot(decision_tree, "WaterMellon_color") # 绘制图
# dict_test = {
# "SeZe": "Wuhei",
# "GenDi": "QuanSuo",
# "QiaoSheng": "ZhuoXiang",
# "WenLi": "ShaoHu",
# "QiBu": "ShaoAo",
# "ChuGan": "RuanNian",
# "MiDu": 0.2,
# "HanTangLv": 0.15
#
# }
#
# # 对预测值进行处理
# decision_tree = {'WenLi': {'ShaoHu': {'ChuGan': {'YingHua': 'No', 'RuanNian': 'Yes'}},
# 'QingXi': {'MiDu': {'<0.3815': 'No', '>=0.3815': 'Yes'}}, 'MoHu': 'No'}}
#
# predict_result = predict(decision_tree, dict_test)
# print("预测的结果为: ", predict_result)
二、读取Excel表格的数据
- 读取Excel表格时,采用绝对路径,相对路径找不到文件(不知原因)
def read_excel_df(url: "绝对路径") -> "DataFrame类型":
"""
:param url: url需要使用绝对路径, 相对路径会报错
:return: 返回Pandas.DataFrame类型数据
"""
return pd.read_excel(url)
pass
二、一 Excel表格数据
1. 西瓜数据集
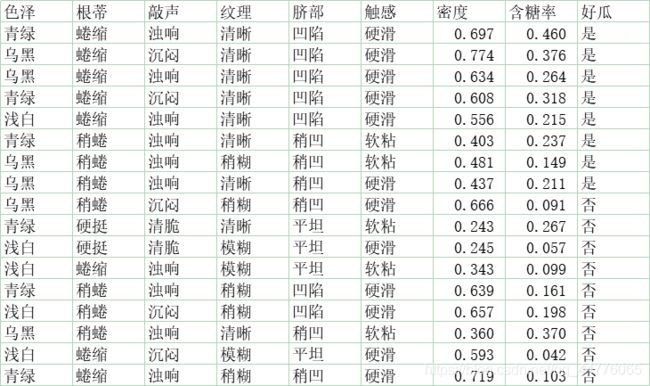
- Chinese
编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否
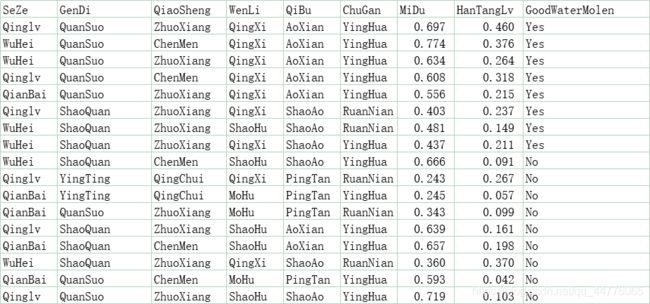
- Enlish
SeZe GenDi QiaoSheng WenLi QiBu ChuGan MiDu HanTangLv GoodWaterMolen
0 Qinglv QuanSuo ZhuoXiang QingXi AoXian YingHua 0.697 0.460 Yes
1 WuHei QuanSuo ChenMen QingXi AoXian YingHua 0.774 0.376 Yes
2 WuHei QuanSuo ZhuoXiang QingXi AoXian YingHua 0.634 0.264 Yes
3 Qinglv QuanSuo ChenMen QingXi AoXian YingHua 0.608 0.318 Yes
4 QianBai QuanSuo ZhuoXiang QingXi AoXian YingHua 0.556 0.215 Yes
5 Qinglv ShaoQuan ZhuoXiang QingXi ShaoAo RuanNian 0.403 0.237 Yes
6 WuHei ShaoQuan ZhuoXiang ShaoHu ShaoAo RuanNian 0.481 0.149 Yes
7 WuHei ShaoQuan ZhuoXiang QingXi ShaoAo YingHua 0.437 0.211 Yes
8 WuHei ShaoQuan ChenMen ShaoHu ShaoAo YingHua 0.666 0.091 No
9 Qinglv YingTing QingChui QingXi PingTan RuanNian 0.243 0.267 No
10 QianBai YingTing QingChui MoHu PingTan YingHua 0.245 0.057 No
11 QianBai QuanSuo ZhuoXiang MoHu PingTan RuanNian 0.343 0.099 No
12 Qinglv ShaoQuan ZhuoXiang ShaoHu AoXian YingHua 0.639 0.161 No
13 QianBai ShaoQuan ChenMen ShaoHu AoXian YingHua 0.657 0.198 No
14 WuHei ShaoQuan ZhuoXiang QingXi ShaoAo RuanNian 0.360 0.370 No
15 QianBai QuanSuo ChenMen MoHu PingTan YingHua 0.593 0.042 No
16 Qinglv QuanSuo ZhuoXiang ShaoHu ShaoAo YingHua 0.719 0.103 No
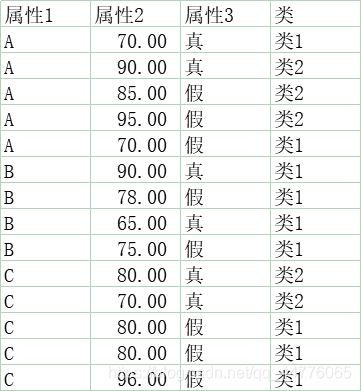
2. 自定义数据集
属性1 属性2 属性3 类
0 A 70 真 类1
1 A 90 真 类2
2 A 85 假 类2
3 A 95 假 类2
4 A 70 假 类1
5 B 90 真 类1
6 B 78 假 类1
7 B 65 真 类1
8 B 75 假 类1
9 C 80 真 类2
10 C 70 真 类2
11 C 80 假 类1
12 C 80 假 类1
13 C 96 假 类1
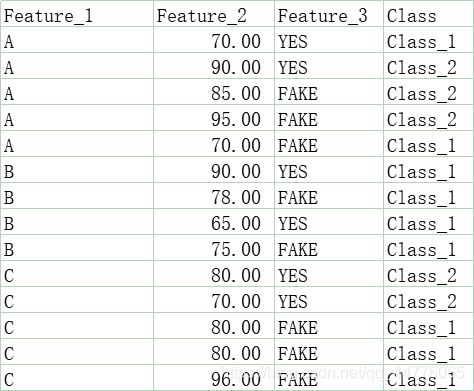
- English
Feature_1 Feature_2 Feature_3 Class
0 A 70 YES Class_1
1 A 90 YES Class_2
2 A 85 FAKE Class_2
3 A 95 FAKE Class_2
4 A 70 FAKE Class_1
5 B 90 YES Class_1
6 B 78 FAKE Class_1
7 B 65 YES Class_1
8 B 75 FAKE Class_1
9 C 80 YES Class_2
10 C 70 YES Class_2
11 C 80 FAKE Class_1
12 C 80 FAKE Class_1
13 C 96 FAKE Class_1
三、绘制 PNG 图片的代码
- 文件名
treePlotter.py - 数据类型为:
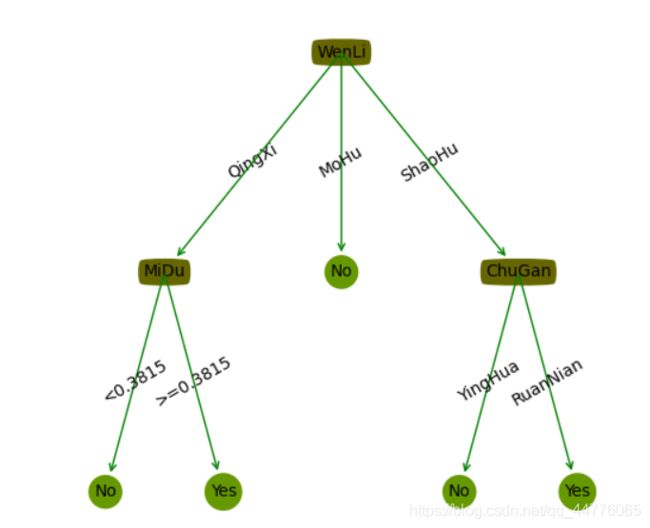
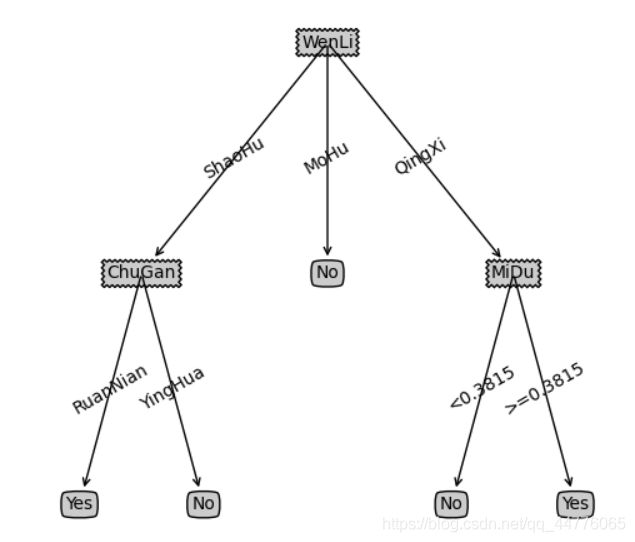
{'Feature_1': {'A': {'Feature_2': {'<77.5': 'Class_1', '>77.5': 'Class_2'}}, 'C': {'Feature_3': {'FAKE': 'Class_1', 'YES': 'Class_2'}}, 'B': 'Class_1'}}
1. 代码
"""
Created on Oct 14, 2010
@author: Peter Harrington
"""
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt): # if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) # this determines the x width of this tree
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0] # the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key], cntrPt, str(key)) # recursion
else: # it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
# if you do get a dictonary you know it's a tree, and the first element will be another dict
def createPlot(inTree, name):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # no ticks
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW
plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '')
# plt.savefig('13数据分布情况')
plt.savefig(str(name))
plt.show()
- 更改节点和树的颜色
# 定义文本框和箭头格式
decisionNode = dict(boxstyle="round4", color='#666600') #定义判断结点形态
leafNode = dict(boxstyle="circle", color='#669900') #定义叶结点形态
arrow_args = dict(arrowstyle="<-", color='g') #定义箭
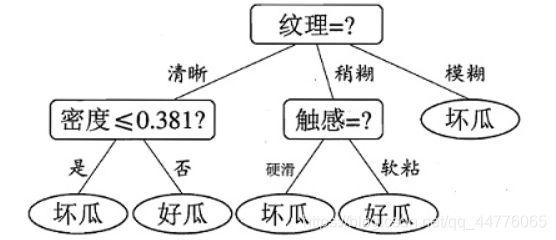
1. 生成的PNG图片
- 生成图片的属性需要是英文
2. 参考西瓜书数据集
四、测试生成树
1. 对测试集中的连续值进行离散化处理
def discrete_data(decision_tree: "建立的生成树", dict_test: "测试例子字典") -> "返回离散化处理后数据集":
"""
对测试集中的连续值进行离散化处理
1. 对于生成树, 第一层字典的值是属性列, 第二层是属性的取值
2. 取出第一层属性作为属性列, 取出第二层的属性作为属性的取值
3. 对测试集进行处理, 取出其中取值是数字(即连续性值)的属性列
4. 如果连续值得属性列 是 这个子树的第一层键(根节点), 比较第二层属性列, 进行连续值离散化处理
1). 大于属性值, 取>=0.2222
2). 小于属性值, 取 <0.222
5. 递归对下一层字典进行处理
:param decision_tree:
:param dict_test:
:return:
"""
# 如果字典树的 属性列 取值不为None
if decision_tree.keys() is not None:
# 取根节点的列属性
root_column = list(decision_tree.keys())[0]
# 取字典值字典的序
second_dict = decision_tree[root_column]
# 取第二层字典键,即是属性的取值
decision_value = list(second_dict.keys())
consecutive_column = []
for key in dict_test.keys():
if isinstance(dict_test[key], (int, float)):
consecutive_column.append(key)
# 对连续进行处理
for conlumn_value in consecutive_column:
# 取测试集的key 与 跟节点的属性进行比较
if root_column == conlumn_value:
for value in decision_value:
# 对测试集字典中的熟悉离散化处理
if value[0: 2] == ">=":
edit_value = value.replace("=", "")
else:
edit_value = value
if isinstance(dict_test[root_column], float):
# 测试集的属性 >= 最佳连续值的时候, 修改测试集中的连续值为: ">=最优连续值"
if float(edit_value[1:]) <= float(dict_test[root_column]):
dict_test[root_column] = ">=" + str(float(edit_value[1:]))
# 测试集的属性 < 最佳连续值的时候, 修改测试集中的连续值为: "<最优连续值"
elif float(str(edit_value)[1:]) > dict_test[root_column]:
dict_test[root_column] = "<" + str(float(edit_value[1:]))
for key in second_dict.keys():
# 第二层字典的取值仍是字典, 需要递归子树处理
if isinstance(second_dict[key], dict):
discrete_data(second_dict[key], dict_test)
return dict_test
pass
2. 递归寻找匹配
# 分类器预测
def match_class(decision_tree: "建立的生成树", dict_test: "测试的数据集") -> "返回判断后的类别":
"""
根据生成的决策时进行预测
1. 对于生成树, 第一层是属性列的值, 第二层是属性的取值
2. 对于测试字典, 第一层是属性列, 第二层是属性列的取值
3. 取生成树第一层属性列, 和第二层属性的取值, 属性值于测试集中对应列进行比较
1). 相等的时候, 判断属性的下一层的值是不是字典, 如果是字典, 则递归子树, 将值保存到class_label中作为结果
2). 下一层不是字典, 而是取值的时候, 赋值到class_label
4. 返回结果集为class_label
:param decision_tree: 建立的决策树
:param dict_test: : 测试集字典
:return: 返回生成树的分类
"""
root_column = list(decision_tree.keys())[0]
second_dict = decision_tree[root_column] # 获取字典树的取值, 第二个字典即属性取值
for key in second_dict.keys():
if key == dict_test[root_column]:
if type(second_dict[key]).__name__ == "dict": # 继续递归
class_label = match_class(second_dict[key], dict_test)
else:
class_label = second_dict[key]
return class_label
pass
3. 对生成树进行预测
def predict(decision_tree: "建立的决策树", dict_test: "测试集的字典类型") -> "返回是 好瓜 或者 坏瓜":
discrete_dict_test = discrete_data(decision_tree, dict_test)
predict_result = match_class(decision_tree, discrete_dict_test)
return "好瓜" if predict_result == "Yes" else "坏瓜"
pass
- 测试数据
dict_test = {
"SeZe": "Wuhei",
"GenDi": "QuanSuo",
"QiaoSheng": "ZhuoXiang",
"WenLi": "QingXi",
"QiBu": "ShaoAo",
"ChuGan": "YingHua",
"MiDu": 0.2,
"HanTangLv": 0.15
}
- 预测结果
predict_result = predict(decision_tree, dict_test)
print("预测的结果为: ", predict_result)
预测的结果为: 坏瓜