决策树算法原理
简介
决策树是一种基本的分类与回归方法。
决策树模型的主要知识有三部分:决策树生成算法、特征选择、剪枝。
决策树生成算法
决策树算法如下:

关键在于第8步,如何选择最优的划分属性。叶子节点的类别(即最终预测的类别值),都标记为叶子节点数据集中类别最多的一类。
特征选择
从众多特征中选择某个特征作为当前节点的标准。常用的选择标准:信息增益、信息增益率、Gini指数。采用不同的评估标准对应不同的决策树算法。
ID3:特征划分基于信息增益
C4.5:特征划分基于信息增益率
CART:特征划分基于基尼指数
相关基础概念
信息熵:描述不确定事件的不确定程度,度量随机变量不确定度。随机变量某个基本事件的概率越大,该随机变量的不确定度越低,信息熵越小。不确定度越高,包含的“信息量”越多,信息熵越高。
假定骰子A和B,掷A正反面的概率:(1/2,1/2),掷B正反面的概率:(4/5,1/5)。直观看,掷A的结果的不确定性更大,因此信息熵越高。而B的大部分可能都是正面,因此不确定性小,信息熵小。
信息熵公式:
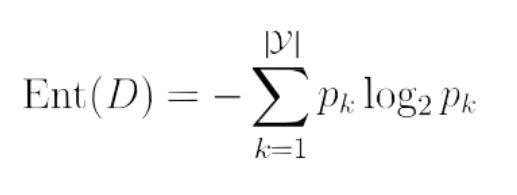
Pk表示的是:当前样本集合D中第k类样本所占的比例。|y|表示结果的种类。
纯度:描述数据集里数据的相似程度,数据集里信息大都是相同的,就是纯度高。数据集里包含的信息很多很杂,就是纯度低。

信息熵与纯度: 信息熵越低,纯度越高。如果样本的属性都是一样的,就会让人觉得这包含的信息很单一,没有差异化,即纯度高;相反样本的属性都不一样,那么包含的信息量就很多,即纯度低。
特征选择方法
信息增益法(ID3算法)
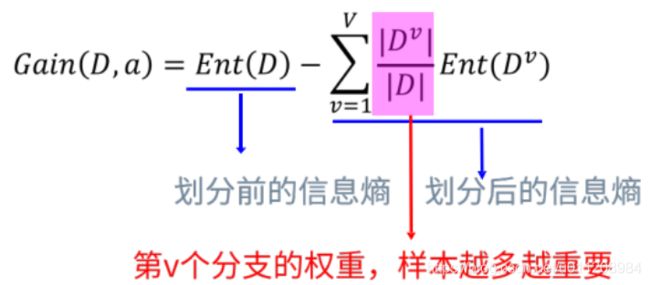
信息增益 = 数据集划分前的信息熵—划分后各子集的信息熵之和
Gain(D,a):以属性a划分数据集时的信息增益。
Ent(D):不划分时总数据集的信息熵。
Dv:属性a取不同值时的数据子集
Ent(Dv):不同数据子集的信息熵。
在进行特征选择时,选择信息增益最大的特征作为当前节点。
缺点:倾向于取值较多的属性。
例如西瓜数据集中的编号属性,一条数据一个取值,取值多,熵低。而总数据集的信息熵Ent(D)是固定的,若公式后面的各子集信息熵之和小的话,就会造成差值大,即信息增益大。若是用信息增益作为选择标准,则编号就会被作为划分节点。
信息增益率法(C4.5算法)
为了解决信息增益的问题,引入一个信息增益率:
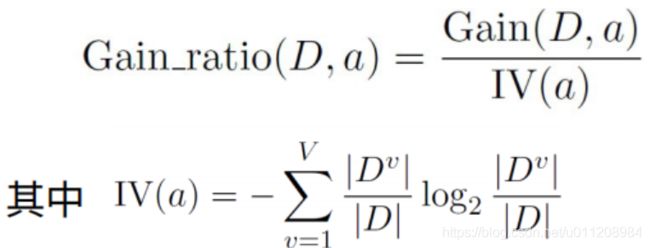
属性a的可能取值数目越多(即V越大),则IV(a)的值通常就越大。IV(a)相当于在计算以a为划分属性时的各取值的子集的熵的和。取值越多则熵越大,加上倒数之后,就会越小。因此取值多的特征乘以的系数小,取值少的特征乘以的系数大。这个系数相当于一个惩罚参数。
缺点:信息增益比偏向取值较少的特征。
基于以上缺点,C4.5算法并不是直接选择信息增益率最大的特征,而是先在候选特征中找出信息增益高于平均水平的特征,然后在这些特征中再选择信息增益率最高的特征。
基尼指数法( CART算法)
用基尼指数划分特征。数据集D的基尼值公式:

Gini(D)反映了从数据集D中随机抽取两个样本类别不一致的概率。Gini(D)越小,数据集D的纯度越高。
属性a的基尼指数公式:
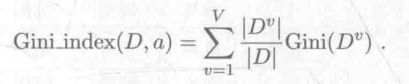
在选择最优划分属性时,选择那个使得划分后各数据子集基尼指数之和最小的属性。和最小,则各数据子集越纯。
三种不同的算法对比
ID3:取值多的属性,更容易使数据更纯,其信息增益更大。
训练得到的是一棵庞大且深度浅的树:不合理。
C4.5:采用信息增益率替代信息增益。
CART:以基尼系数替代熵,最小化不纯度,而不是最大化信息增益。
详见决策树中的ID3, C4.5, CART算法及其优缺点,写得很棒!
ID3算法详解
解释:在整体数据集上计算根节点处信息熵,然后依次计算各个属性划分的数据子集的信息熵,用根节点信息熵–某属性节点的信息熵=信息增益,根据信息增益进行降序排列,排在前面的就是第一个划分属性,其后依次类推,这就得到了决策树的形状,也就是怎么“长”了。
即:信息量大的节点先排在前面,各节点先后顺序根据信息增益排序。
详细计算示例如下:
1)先计算整体数据集根节点信息熵:
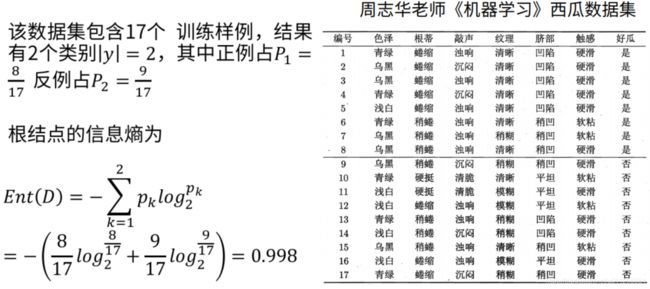
2)计算“色泽”属性的信息增益。

可以看到,D1集合里好瓜坏瓜的比例差不多,更不好确定,因此信息量越大,即信息熵越大。而D2集合里正例比反例多点,即偏向于大多数是正例,不确定性小,纯度越高,信息量越小,信息熵越低。D3集合更是大部分都是坏瓜,纯度更高,信息熵更低。
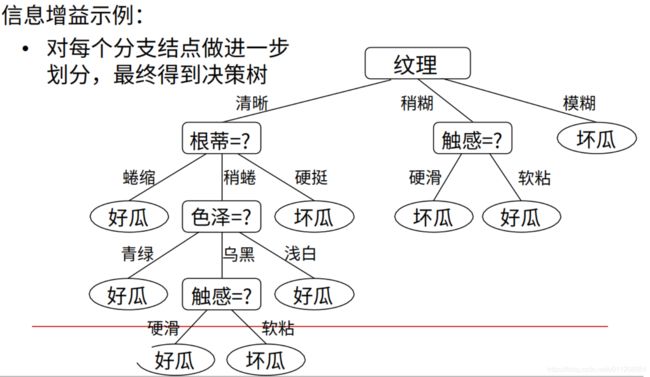
3)计算其他属性的信息增益。根据信息增益大小,确定决策树头节点为“纹理”。

4)生成其余节点。
在上一步,纹理节点将数据集划分成了三部分,在这些子数据集上做同样的操作:计算除纹理节点以外的属性的信息增益,选出信息增益最大的作为下一个节点。其他节点类推。
剪枝
解决过拟合问题。分为预剪枝和后剪枝。预剪枝常用。
参考:
周志华《机器学习》
机器学习算法(3)之决策树算法