常见查找和排序算法汇总
主要内容:
顺序查找、折半查找-------查找算法
冒泡排序、简单选择排序、直接插入排序、希尔排序、归并排序、快速排序、堆排序------排序算法
一、查找
1、顺序查找
从最后一个记录开始,逐个进行比较,若相等则查找成功,否则查找失败。
//顺序查找 a[1 - len]
int Sq_Search(int a[],int key,int len)
{
int i;
//哨兵,使内循环不用判断数组是否越界,提高程序运行效率,减少查找时间
a[0] = key;
for(i = len;a[i] != key;i--) ;
return i;
}
2、折半查找
在折半查找中,查找一个值相当于在一个满二叉树中查找,计算平均查找次数时可利用满二叉树性质。
//折半查找 a[0 - len-1]
int Bi_Search(int a[],int key,int len)
{
int i,low,mid,high;
low=0;high=len-1;
while(low<=high)
{
mid = (low+high)/2;
if(a[mid] == key)
return mid;
else if(a[mid] > key)
high = mid-1;
else
low = mid +1;
}
return -1; //查找失败返回-1
}
二、排序(升序)
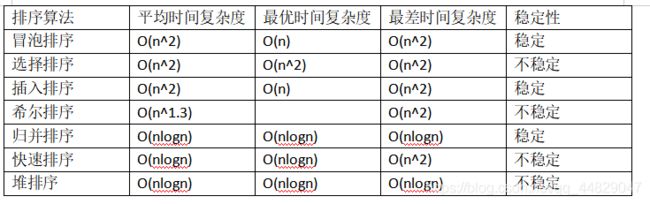
1、冒泡排序
排序思想:从前往后依次比较前后两个相邻元素,将大的置于右端,小的置于左端;如此,每轮可以将一个值置于其最终位置,n-1轮后数组有序。
稳定性:稳定,当元素相等时,并不会发生交换
空间效率:O(1)
平均情况:O(n^2)
最坏情况:O(n^2),序列逆序时
最优情况:O(n),序列有序时
代码:
#include运行结果:
排序思想:每轮从待排序序列中选择一个最小值放到该序列的最左端,经过n-1轮后,数组有序。
稳定性:不稳定,如 2 - 2 - 1
空间效率:O(1)
平均情况:O(n^2)
最坏情况:O(n^2)
最优情况:O(n^2),比较次数是固定的,所以最优最差没有数量级的差距,时间复杂度不受数据初始状态影响
代码:
//选择排序
void Select_Sort(int a[],int n)
{
int i,j,min; //min用于获取最小值的下标
//使用数组下标来记录最值所在位置有时非常方便
for(i = 0;i<n-1;i++)
{
min = i;
for(j = i+1;j < n;j++)
{
if(a[j]<a[min])
min = j;
}
swap(a[i],a[min]); //交换
}
}
3、直接插入排序
排序思想: 从后往前进行比较,依次将元素插入到前面已经排好序的子序列中。
稳定性:稳定,从后往前比较,不会出现相同元素相对位置的变化
空间效率:O(1)
平均情况:O(n^2)
最坏情况:O(n^2),表中元素顺序与结果相反
最优情况:O(n),表中元素已经有序
代码:
//插入排序
void Insert_Sort(int a[],int n)
{
//int B[11] = {0,1,7,5,3,9,8,2,3,0,6}; 0单元做哨兵
//n = 10
int i,j;
for(i = 2;i <= n;i++)
{
a[0] = a[i]; //哨兵,避免数组越界
for(j = i-1;a[j] > a[0];j--)
{
a[j+1] = a[j];
}
a[j+1] = a[0];
}
}
4、希尔排序
排序思想: 将排序序列中相隔某个增量的记录组成一个子表,对各个子表分别进行直接插入排序,当整体已经基本有序时,对整个序列再进行一次直接插入排序,此时增量为1。
增量的选择:用总长除以2,不断循环,直到步长为1
稳定性:不稳定,当相同元素被划分到不同的子表时,相对位置可能会变
空间效率:O(1)
平均情况:O(n^1.3) ,比较特殊
最坏情况:O(n^2)
最优情况:应该是O(n),和直接插入排序一样
代码:
//希尔排序
void Shell_Sort(int a[],int n)
{
int i,j,d;
for(d = n/2;d>=1;d=d/2) //步长,最后的步长为1
{
for(i = d+1;i <= n;i++) //对步长一致的序列进行插入排序
{
a[0] = a[i]; //插入排序中的哨兵
for(j=i-d;j>0&&a[j]>a[0];j=j-d)
a[j+d] = a[j];
a[j+d] = a[0];
}
}
}
待排序列:
49 - 38 - 65 - 97 - 76 - 13 - 27 - 49 - 55 - 04
第一趟排序结果:
13 - 27 - 49 - 55 - 04 - 49 - 38 - 65 - 97 - 76(d=5)
后面类似
5、归并排序
排序思想: 将两个或两个以上的有序表组合成一个新的有序表
稳定性:稳定
空间效率:O(n),合并操作需要n个额外的单元
平均情况:O(nlogn)
最坏情况:O(nlogn)
最优情况:O(nlogn),固定log2^n趟排序,每趟归并O(n),时间复杂度不受数据初始状态影响
代码:
//归并排序
int b[15];
void Merge_Sort(int a[],int low,int high)
{
int i,j,l,k,mid;
if(low < high)
{
mid = (low + high)/2;//将当前序列一分为二,看作2个序列进行归并
Merge_Sort(a,low,mid);//让左序列有序
Merge_Sort(a,mid+1,high);//让右序列有序
for(i=low;i<=high;i++) //复制整个序列,有=号
b[i]=a[i];
//开始归并左右2个序列
for(i=low,j=mid+1,k=low;i<=mid&&j<=high;k++)
{
if(b[i] <= b[j])//加=号是为了让算法具有稳定性
a[k] = b[i++];
else
a[k] = b[j++];
}
while(i<=mid) //左序列还要剩余
a[k++] = b[i++];
while(j<=high)//右序列还要剩余,2个while只会运行其中一个
a[k++] = b[j++];
}
}
6、快速排序
排序思想: 任取一个元素pivot(一般是首元素)作为枢轴,通过一趟排序将待排序记录分割成两个部分,一部分小于pivot,一部分大于等于pivot,然后对这两部分重复上述过程,直至整个序列有序。每部分只有一个元素或为空时就是结束条件。快速排序是所有内部排序算法中平均性能最好的算法。
稳定性:不稳定。若有相同两个元素在右端区间,且均小于基准值,交换后,相对位置会改变,如 3 1 1
空间效率:O(log2^n),与递归调用的最大深度一致
平均情况:O(nlogn)
最坏情况:序列基本有序或有序时,退化成冒泡排序->O(n^2)
最优情况:O(nlogn),均衡划分子区间,使子问题都不大于n/2
代码:
//快速排序
void Quick_Sort(int a[],int left,int right)
{
int i,j,k;
//先左后右检索
//递归终止条件,当只有一个数或者没有数排序时return
//一个数:left==right 没有数: left>right
if(left>=right)
return ;
k = i = left; //选第一个数为临界值
j = right;
while (i < j)
{
//必须加 i< j,不然会出现数组越界的问题
//不加 = 号,i 会一直停止在第一个数上
while (a[j] >= a[k] && i < j)
j--;
while (a[i] <= a[k] && i < j)
i++;
//加不加if都行
swap(a[i],a[j]);
}
// j 先动 a[j]一定会大于等于 a[k] ,可直接交换
swap(a[k],a[i]);
QuickSort(a,left,i-1); //递归排序剩余序列
QuickSort(a,i+1,right);
}
7、堆排序(大堆:父节点大于孩子节点的二叉树)
排序思想: 把n个元素建成大堆,堆顶是最大值。输出堆顶后将堆底元素放入堆顶,调整堆变回至大堆,重复该过程至元素有序。
关键:
1、如何将无序序列建成大堆。(自下向上逐步调整为大堆)
2、输出堆顶后,如何调整堆变回大堆。(从根节点开始向下调整为大堆)
稳定性:不稳定,调整时可能把相同关键字元素调整到前面,如1-2-2
平均情况:O(nlogn)
最坏情况:O(nlogn)
最好情况:O(nlogn),固定有n-1次向下调整操作,每次调整为O(h),所以没有数量级差距。
时间复杂度不受数据初始状态影响
代码一:
//堆排序
void HeadAdjust(int a[],int k,int len)
{
a[0] = a[k]; //0单元暂存根节点
for(int i = 2*k;i <= len;i*=2) //不是叶子节点时循环
{
if(i < len && a[i] < a[i+1])
i++; //取值较大节点的下标
if(a[0] >= a[i]) //根节点大于两个孩子,不用调整,结束
break;
else //将值更大的孩子节点调整到根节点上
{
a[k] = a[i];
k = i; //便于继续向下调整
}
}
a[k] = a[0]; //放入最终位置
}
void BuildMaxHeap(int a[],int len)
{
for(int i=len/2;i>0;i--) //从最后一个非叶节点向上调整 *********
HeadAdjust(a,i,len);
}
void HeadSort(int a[],int len)
{
BuildMaxHeap(a,len);
for(int i=len;i>1;i--) //0单元暂存值.。
{
swap(a[i],a[1]); //输出堆顶元素,与堆底交换
HeadAdjust(a,1,i-1); //调整剩余的i-1个元素为大堆
}
}
代码二:
void DownAdjust(int a[],int i,int n)
{
int t;
while(i*2<=n)//不是叶子节点,且不是一个大堆
{
if(a[i*2]>a[i]) //如果左孩子比节点大
t = i*2;
else
t = i;
if(i*2+1<=n) //如果右孩子存在 **********
{
if(a[i*2+1]>a[t]) //如果右孩子大于左孩子和节点
t = i*2+1;
}
if(t != i) //需要向下调整
{
Swap(a[t],a[i]);
i = t;
}
else //已经是大堆,结束调整
break;
}
Print(a,8);
}
void CreatMaxHeap(int a[],int n)
{
int i;
for(i=n/2;i>=1;i--) //从最后一个非叶节点向上调整 *********
DownAdjust(a,i,9);
}
void HeapSort(int a[],int n)
{
int i,j;
for(i=n;i>=2;i--) //i=2时,交换后排序就完成了
{
Swap(a[1],a[i]);
Print(a,8);
DownAdjust(a,1,i-1);
}
}
