【FCOS】FCOS理论知识讲解

1 FCOS是什么

FCOS发表于ICCV 2019，是常用的无需锚框(先验框、anchor)的目标检测算法之一。

1.1 核心思想

核心思想：将铺设锚框变为铺设锚点，进行物体检测。

所谓铺设锚框，又称为Anchor-Based，是指在输出特征图上的每个像素的位置，放置几个预先定义的anchor框，在网络训练过程中，对这些anchor框进行分类与回归。
通过GT框和这些anchor框计算IoU，依据设定的阈值条件来定义正负样本，典型的有YOLOv3。

所谓铺设锚点，又称为Anchor-free，如下图所示，将原有的 对锚框进行分类与回归，变为对锚点进行分类与回归，其中回归是预测锚点到检测(GT)框上下左右四条边界的距离，典型的有FCOS。

1.2 Anchor-Based缺点

• Anchor-Based方式，检测性能对于anchor的大小、数量、长宽比 都非常敏感，通过改变这些超参数Retinanet在COCO benchmark上面提升了4%的MAP。
• 固定size和aspect ratio的anchor损害了检测器的普适性，导致对于不同任务，anchor可能需要重新设置大小和长宽比。
• 为了达到更高的召回率(查全率)，需要生成大量的anchor(FPN约18万个)，但是大部分的anchor在训练时标记为负样本(negative)，造成了样本不均衡问题。
• 在训练中，需要计算所有anchor与真实框的IoU，这样会消耗大量内存和计算资源。
  

1.3 FCOS优点

• 检测问题被统一到 FCN-solvable 的问题，可以简单地重用其他任务的idea，如语义分割。
• anchor-free方式，不需要像anchor-based那样大量调整参数，使训练更为简单。
• 由于不需要计算IoU，节省了大量算力和内存。
• 提出了一些关于交叠区域的解决方法和思考。
• 模型部署会受到两种限制，一种是计算量的限制，一种是I/O 带宽的限制。anchor-free方式相比于anchor-based方式，对部署更友好一些。

2 FCOS 网络总解

2.1 初始版本网络结构

早期的FCOS网络结构如下图所示：

FCOS采用FPN结构，backbone的C3、C4、C5特征层作为FPN的输入，FPN生成P3,P4,P5,P6,P7特征图，送入后续的检测头Head。

每个Head包含3个分支：

• classification分支：预测类别，图中的C表示类别数，相当于C个二分类
• regression分支：回归位置，图中的4表示：l,t,r,b，预测锚点到检测框上下左右四条边界的距离
• center-ness：中心度，一个锚点对应一个中心度，用于锚点相对于检测框中心性的判断

在检测子网络Head中，分类分支和回归分支都先经过了4个卷积层进行了特征强化。

早期版本，在分类分支中，既包含 正、负样本锚点的 类别预测分支，又包含正、负样本锚点中心性判断的center-ness分支，用来强化检测结果；

回归分支 用来回归正样本锚点到检测框上、下、左、右四个边界的距离 。

2.2 分支改进后网络结构

center-ness分支，早期版本是和classification分支一起，如上图所示，后来大家发现center-ness分支和regression分支一起效果更好，如下图所示。

感谢 太阳花的小绿豆 画的更详细的网络结构图：

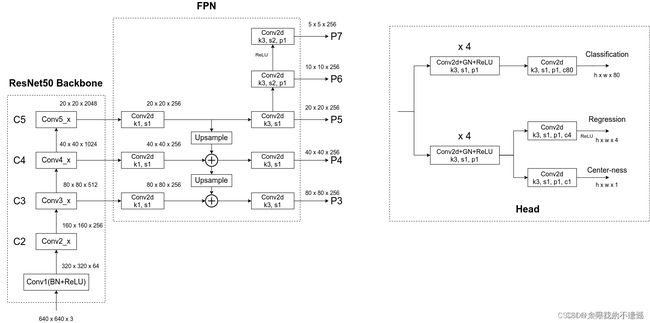
2.3 损失函数

以最新版本损失函数为例，Head总共有三个输出分支：Classification、Regression和Center-ness。故损失由分类损失$L_{cls}$、定位损失$L_{res}$以及center-ness损失$L_{ctrness}$三部分共同组成：

分类损失$L_{cls}$采用 BCELoss + Focal Loss ，计算损失时所有样本都会参与计算（正样本和负样本）。
定位损失$L_{res}$采用GIoU loss(早期采用 IoU loss），计算损失时只有正样本参与计算。
center-ness损失$L_{ctrness}$采用 BCELoss，计算损失时只有正样本参与计算。

更详细的centerness分支可在第7节中看到。

3 正样本、负样本、模糊样本的定义

使用候选框进行目标检测时，也就是anchor_based方式，候选框中是否包含目标就是判断正负样本的的准则。
有目标的就是正样本，没有目标的就是负样本。

对于使用anchor_free方式的FCOS，它是把特征图上的每个点作为一个样本，如果这个点落在任何一个GT框内，它就是正样本，否则它就是负样本。

在正样本中，存在一个点落在多个GT框中的情况，如下图所示，这个点称之为模糊样本(ambiguous)。

此时，有两个问题：

• 特征图上的点怎么知道它是在原图上的GT框内还是外呢？
  回答：见第4节分析。
• 一个点恰好只落在一个框内，此时它就去负责预测这个GT框，那模糊样本预测谁呢？怎么处理呢？
  回答：一个点落在多个GT框中，取最小的那个GT框作为回归目标，此外，利用FPN进行多尺度预测会极大程度上减少这种情况的发生。具体细节在第6节介绍。

下面分别回答。

4 特征图上的点映射回原图

对于特征图 $F_i\in R^{H\times W\times C}$，其相对于输入图片的stride定义为 $s$ (举个例子，特征图宽高是40x40，输入图片宽高是320x320，那么 s 等于8)。

另外记GT框的信息为 $B_i$，$B_i=\{x_0^{(i)},y_0^{(i)},x_1^{(i)},y_1^{(i)},c^{(i)}\}$，其中 $(x_0^{(i)},y_0^{(i)})$ 和 $(x_1^{(i)},y_1^{(i)})$ 分别表示GT框的左上角和右下角顶点坐标， $c^{(i)}$ 是GT框的类别。

对于特征图$F_i$上的每个点坐标$(x,y)$ ，可以用如下公式把它映射到原输入图像上：
$$(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys)$$

5 锚点回归目标值

注意： 锚点落在任何GT框的内部，就认为这个锚点是正样本，并负责预测这个GT框，在映射回原图后的该点直接回归目标框，而不是把这个点看成目标框的中心点进行回归。

锚点的回归目标值计算公式如下图所示，其中$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$是锚点距离物体真实标注框左、上、右、下边界的距离。
在regression分支中，每个锚点预测一个4维向量，即$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$。

网络能把每个锚点距离真实标准框的距离预测的越准，说明网络检测效果越好。

此处的$(x,y)$应该是特征图上的锚点映射到原图上的位置。
这里用stride (上图中的s) 进行缩放，使得不同尺度的物体，回归目标值都在一定范围内，避免训练过程中可能出现的梯度爆炸。
由于4个回归值要大于0，最后的输出采用ReLU来保证回归值的范围为(0, +∞)。

6 模糊样本的处理

锚点落在多个GT框的区域内，则称其为模糊样本（ambiguous）。

以一个像素落在两个GT框的情况为例，选择的原则是：选择面积最小的一个GT框作为它训练用的回归目标。
为什么选面积最小的GT框作为它的回归目标？我的理解是：回归小框的像素点本来就少，大的GT框肯定有更多的点去回归的！

思考： 有点草率了，应该先有点什么限制或减少这种情况出现！
回答： 模糊样本的出现，大部分是由于物体重叠造成的，但是重叠的物体多数大小是不同的，所以 FPN特征金字塔 闪亮登场。

启发于anchor-based方法，采用FPN时会将不同大小的anchor放置在不同大小的特征图上，特征图越小，感受野相应更大，用来检测更大的物体。同样地，这种设计理念可以用在FCOS模型上。

FCOS采用5个大小不同的特征图 $P_3,P_4,P_5,P_6,P_7$，其对应的stride分别是8,16,32,64,128。辅助理解：$2^i$。

为了减少尺度差异大的物体重叠，对于anchor-based方法，由于是根据anchor和GT框的IoU来进行匹配，所以很自然地将大小不同的GT框分配到不同的特征图。

而FCOS直接通过限制不同特征图上目标回归值来达到这一目的。
具体来说，每个特征图 $P_i$ 会设定一个回归值的下限值 $m_{i-1}$ 和上限值 $m_i$ ，作为其回归距离限制。

对于特征图$F_i$上的每个点坐标$(x,y)$ ，满足$max(l^{\ast },t^{\ast },r^{\ast },b^{\ast })>m_i$ 或 $min(l^{\ast },t^{\ast },r^{\ast },b^{\ast })<m_{i-1}$，那么在这个特征层就将其视为负样本，不再进行回归。论文中 $m_2,m_3,m_4,m_5,m_6,m_7$ 分别设定为0,64,128,256,512,+∞。
也就是特征图 $P_3$ 覆盖的是[0,64]之间的目标回归值，而 $P_7$ 则是负责512以上的目标回归值。

7 Center-ness分支

作者在使用了多尺度检测后发现仍然和anchor-based的检测器有很大差距，发现FCOS存在大量的低质量的检测框。这是由于把中心点的区域扩大到整个物体的边框，经过模型优化后可能有很多中心离GT box中心很远的预测框。

于是，FCOS在regression分支的末尾添加了一个额外的center-ness分支(早期放在classification分支，但是放在regression分支效果更好)来抑制一些检测框：由偏离目标中心的锚点 所预测的低质量检测框。

中心性预测分支center-ness，动机在于如果一个锚点距离物体标注框中心点越近，锚点的回归目标值（锚点距离标注框左、上、右、下四个边界的距离）就越一致，回归难度较低，回归效果会越好。

center-ness分支只预测一个值：当前位置与要预测的物体中心点之间的归一化距离，值在[0, 1]之间，距离物体中心点越近，得分越高。下图给出了可视化效果，其中红色和蓝色值分别1和0，其它颜色介于两者之间，从物体中心向外，center-ness从1递减为0。

给定回归的$target=(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$，center-ness的target label定义为$centernes{s}^{\ast }$：

由于$centernes{s}^{\ast }$值在0~1之间，训练过程中可以采用 BCE损失函数 进行优化。

可以看出，当loss越小时，centerness就越接近1，也就是说回归框的中心越接近真实框。

注意： 在测试阶段，最终的置信度为center-ness和分类概率的乘积

8 后续改进

8.1 center sampling

• 原始论文：GT bbox 内的点，分类时均作为正样本（下图上面小图的所有黄色区域）。
• 改进 trick：只有 GT bbox 中心附近的 radius * stride 内的小 bbox（可以叫 sub box）内的点，分类时才作为正样本（下图下面小图的黄色和绿色区域）。

也就是要落在：$(x-rs,y-rs,x+rs,y+rs)$这个框内，作者通过消融实验发现在coco数据集上 r 取1.5效果最好。

8.2 centerness 分支的 centerness计算

• 原始论文：利用 l，t，r，b 计算 centerness。小目标的 centerness 值比较小，最终 cls 分数很容易被阈值卡掉。
• 改进 trick：直接用 IoU

8.3 regression分支的loss

• 原始论文：IoU loss
• 改进 trick：GIoU loss

8.4 bbox loss weight

• 原始论文：平权
• 改进 trick：用 centerness 分支的 target，即离gt中心越近，权重越大。

8.5 norm on bbox

• 原始论文：reg分支最后使用exp操作
• 改进 trick：reg分支最后使用relu操作

8.6 开发板上部署时优化策略

• 使用轻量型网络，例如mobilenetv2，Efficientnet对backbone进行替换。
• 使用BiFPN替换FPN。BIFPN给各个层赋予了不同权重去进行融合，让网络更加关注重要的层。BIFPN还减少了一些不必要的 层的结点连接。
• 将Efficientnet中的swish激活函数替换成ReLu，去掉backbone中的sigmoid结构

9 感谢链接

https://zhuanlan.zhihu.com/p/468494402
https://zhuanlan.zhihu.com/p/156112318
https://zhuanlan.zhihu.com/p/443367551
https://zhuanlan.zhihu.com/p/104236411
https://zhuanlan.zhihu.com/p/62869137
https://blog.csdn.net/qq_37541097/article/details/124844726