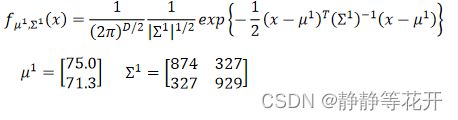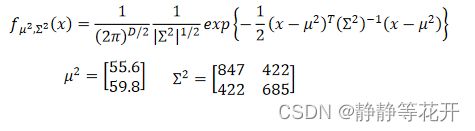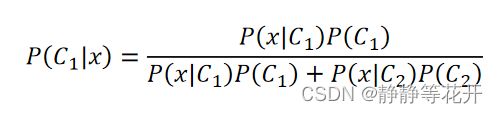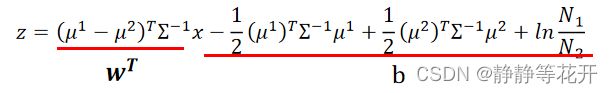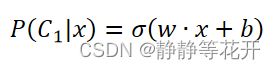机器学习笔记 Classification 分类
Classification 分类
- 分类问题的应用
- 能否用Regression去解决Classification?
- 理想的分类模型
- 取球例子
- 宝可梦的分类
- 分类function进一步处理
- 扩展:为什么统一∑后,分界线变成线性?
分类问题的应用
输入一只宝可梦,输出他对应的属性分类

如何把宝可梦当作input输入呢?我们需要将宝可梦数值化。
用一个vector矢量去表示一只宝可梦,vector可以包括HP血量、Attack攻击力、Defence防御力、Speed速度等。
所以接下来的问题就是找到一个function,输入一个vector,输出对应的属性值。
能否用Regression去解决Classification?
以某一个二分类问题作为例子:
训练model时,分类为Class one时我们的function输出目标为1;分类为Class two时我们的function输出目标为-1。(输出的目标不会正好是1或-1,所以将0为分界线)
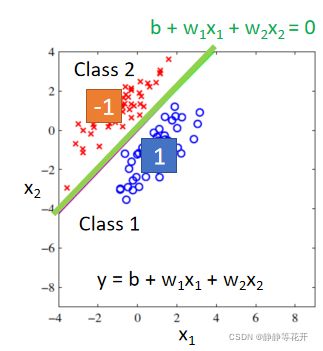
上图,绿色的线是函数值等于0的部分,在函数下面大于0归类为Class one,函数上面小于0归类为Class two。
在这种情况下,分类效果还不错,再看下图:
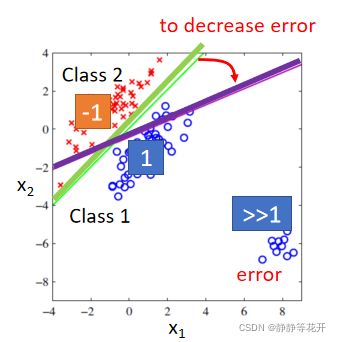
绿的的线可以很好的分类Class one和Class two,但我们在Regression的时候往往更倾向于得到紫色的线。因为存在右下角的点,他们是远大于1的点,Regression在train过程中,会倾向于减少他们带入function后输出的值(这些点是太过正确的点,但是对Regression来说是error,所以会惩罚这些点),所以会相对绿色的线往下偏一些,但是紫色并不能很好的分类Class one 和Class two。
另一个潜在的问题:
当你分类3个Class时,规定Class one输出1,Class two输出2,Class three输出3。这样其实潜在的定义了Class one和Class two会比较相似,Class one和Class three相差比较大,但是事实并非如此。
所以,不建议用Regression解决Classification问题。
理想的分类模型
三部曲:
(1)给出Model(函数function的集合)
(2)定义损失函数Loss Funtion(定义函数的好坏)
(3)从Model中寻找最佳function
理想的分类function输出应该是离散的。

如图,function中存在某一个函数g(x),当g(x)达到某一要求就输出Class 1,否则class 2。
function的样式确定了,接下来就是确定损失函数Loss Function

如上图,损失函数定义为分类样本正确的个数
接下来我们依靠损失函数去找best Function(最佳function)
取球例子
现已知
从Box 1抽取球的概率P(B1)=2/3
从Box 2抽取球的概率P(B1)=1/3
从Box 1抽取篮球的概率P(Blue|B1)=4/5
从Box 2抽取篮球的概率P(Blue|B2)=2/5
从Box 1抽取绿球的概率P(Green|B1)=1/5
从Box 2抽取绿球的概率P(Green|B2)=3/5
问:抽取到了篮球,它是来自B1的概率。
这可以用概率论的贝叶斯公式得出:
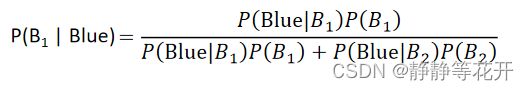
抽取到了篮球,它是来自B1的概率的问题,可以近似看为,我抽取到了一个样本,他是Class 1的概率。
宝可梦的分类
基于上述例子,我们把Box 1,Box 2看作是Water(水系)和Normal(一般系)

假设我们将140只宝可梦数据作为training data(训练集)。
training data中有79只Water,61只Normal
可以得到:
P(C1)=79/(79+61) = 0.56–Water系的占比
P(C2)=61/(79+61)=0.44–Normal系的占比
接下来提出问题:
我们现在拿到一个training data里不存在的样本x(一只海龟),如何判断它属于Water系得概率?

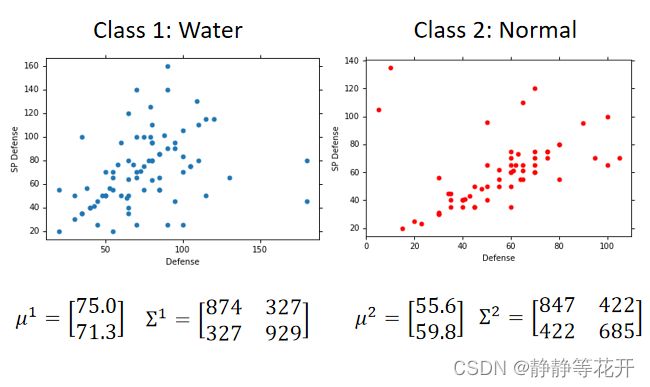
为了简化问题,我们只考虑宝可梦的Defense和SP Defense两个属性
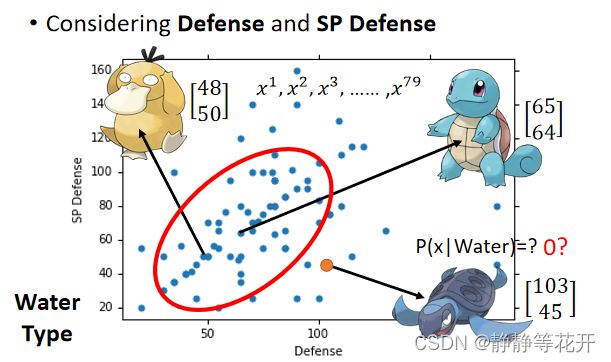
画出图像,海龟样本在图中是不存在的,是否概率就为0呢?
当然其概率不为0,只是training data中不存在。
接下来,我们假设上述图中的点遵从高斯分布(正太分布)
两个问题:
(1)假设为其他分布,如0-1分布也行。只是最后模型准确率不同。假设该模型服从什么分布是人脑去决定的,相当于调参。
(2)在假设为遵从高斯分布后,就可以从training data的数据去推出该高斯分布的概率密度函数f(x),从而将新样本点输入,得到的值就是Water系或者Normal的概率。
(3)概率密度函数f(x)的值就是该样本点x附近出现的概率,在本案例表现为是某一系的概率。
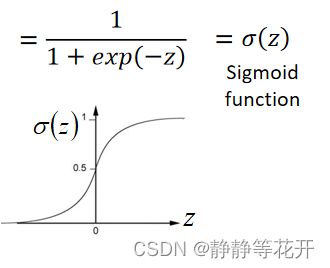
高斯分布概率密度函数:

这里表示u均值,∑表示协方差矩阵,两者都是矩阵matrix
对协方差矩阵含义不清楚可以看:
https://blog.csdn.net/qq_45351128/article/details/124526134
该高数分布概率函数图像由u和∑共同决定;u决定最大值在哪,∑决定陡峭程度(离散程度)。
如下图,不同的u和∑对应不同的图像
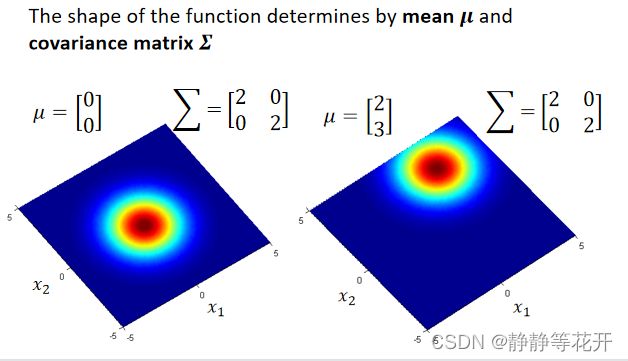
那么怎么通过training data去找到u和∑呢?
通过training data去确定高斯函数概率密度函数,另一角度就是高斯函数如何去生成这些点,靠近中心点(样本较多)时概率密度函数值大,远离中心点(样本较少或者没有)时概率密度函数值小。
为了实现上述功能,定义了Likelihood函数:

将所有training data样本点x1……xn的概率密度函数相乘,找到使得该函数取得最大值的u和∑。

最后求得:
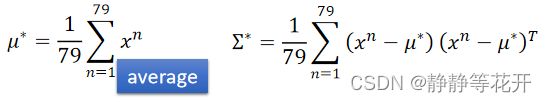
对于training data79只Water系样本,61只Normal系样本求得各自得u和∑。
fu,∑(x)表示个样本点的分布概率情况,所以具体的的概率值指的是,在Class i中抽到x的概率,可表示为:P(x|Ci)
所以我们得到了:

当P(Ci|x)>0.5就归为Water 系,否则为Normal系。
到此,分类宝可梦的function就找出来了
具体的高斯分布函数图如下图:

最后的结果准确率为0.47,不是很理想。
分类function进一步处理
对于例子中的两类各自的高斯概率密度函数都有不同的∑。
为了简化计算使用更少的参数,我们统一使用一样的∑。使用更少的参数,也一定程度上上减少了function过拟合的情况。
个人理解:
∑协方差矩阵另一方面也表示各输入feature(特征)之间的相关程度。对于不同的类别的feature,它们之间的相关性比较相似,所以没必要对各类都使用不同的∑;对不同的类使用不同的∑,这个∑也许会根据输入样本而造成不同,产生过拟合。
当使用同样的∑之后,linkehood发生了变化:

对于u和∑的确定:
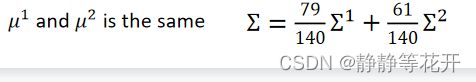
u1和u2不变,∑变为∑1和∑2的期望
统一∑之后,准确率变成了73%
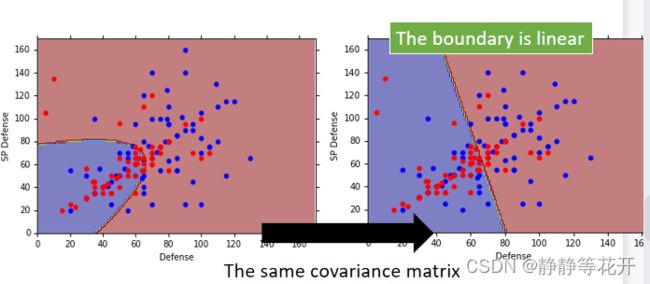
最终,function确定的三部曲为:

扩展:为什么统一∑后,分界线变成线性?
对于z,我们进一步推导:

z的前半部分进一步推导:
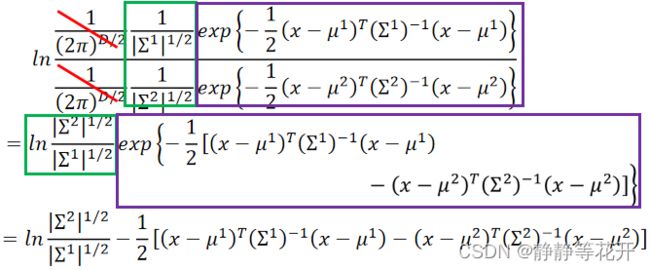

将推导后结果带入z:
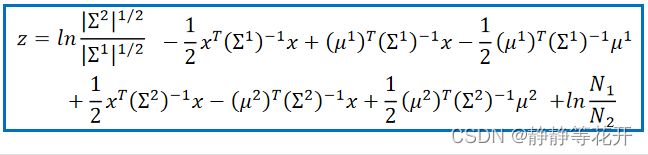
又因为∑都相同,所以:

wT部分得到的是一个矩阵;而b是多个二次型相乘得到的是一个数。
所以,
括号里面类似一个线性函数,所以统一∑后分界线是linear。
以后对于二分类问题,我们可以把问题简化为:如何找到w 和 b,以及u和∑