模型加速之INT8量化原理及实践（基于TensorRT）

一、模型量化：

1、量化的定义是将网络参数从Float-32量化到更低位数，如Float-16、INT8、1bit等。

2、量化的作用：更小的模型尺寸、更低的功耗、更快的计算速度。下图是不同数据结构比较及执行基本运算时的计算消耗。

3、浮点数均匀间隔映射的量化过程称为均匀量化，否则是非均匀量化，也可以叫作线性量化和非线性量化。

4、被映射区间关于0点对称分布称为对称量化，比如需要映射的数值范围[-10000,30000]，映射区间为[-127,127]，映射时选取被映射区间为[-30000,30000]，否则是非对称量化。

5、按量化过程发生的阶段可以分为训练时量化(quantization-aware training)、微调时量化(quantization-aware fine tune)和训练后量化(Post-training quantization)。

二、二值量化XNOR

        在介绍INT8的量化前，我们先看一个相对简单的二值量化，我们以经典算法XNOR为例。

        对于卷积网络，最基础的卷积计算可以表示成以下形式：

         其中w代表卷积核的权重，a代表上一个激活函数的输出值，代表一种非线性运算，z为输出结果。

        在二值量化过程中，需要将w和a转换成二值方式表示：

         其中bw和ba是二值表示下的权重和激活值，是尺度，是浮点数。

         经过转换后的卷积计算过程变成了如下形式：

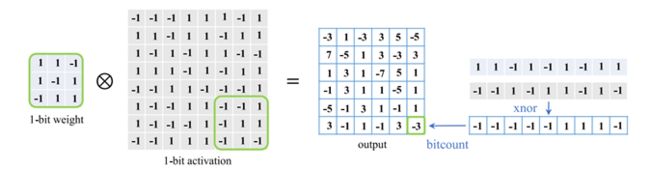
         其中过程可以由下图表示：

         对位运算熟悉的可以发现，这就是一个异或运算，远比32位浮点数的运算简单的多。

        得到的结果还需要经过下式进一步操作：

         这样就实现了前向传播的量化，但是如果需要反向传播这样还不够。

        反向传播需要逐层求导，显然sign的导数在大多数地方都为0或者不存在。为了解决这个问题，STE(Straight-throught estimator)技术出现了，通过一个以下函数将输出x直接映射成了梯度，并将梯度限制在[-1,1]之间：

         这样子有了梯度，结合原先的浮点数就可以实现反向传播（前向传播在量化参数的同时需要保存一份用于反向传播）。

三、TensorRT INT8原理

        清楚了二值量化的基本原理后，我们来看TensorRT是怎么实现INT8量化的，下图是INT8量化的基本流程。

         类似二值量化，INT8量化其实也是一个映射过程，最简单的方式是直接将tensor按照[-|max|,|max|]映射到[-127,127]。

        其中c表示tensor中最大值的绝对值，对于INT8映射，n=8。

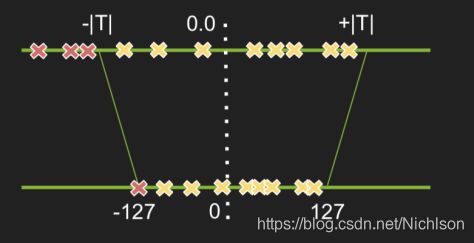
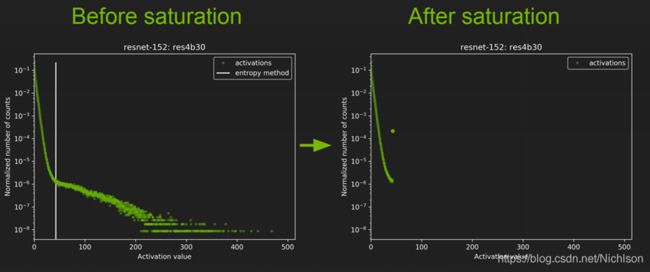
        但是这种方式容易放大噪声，为了降低噪音的影响，TensorRT的改进做法是从127和|max|之间选择好一个阈值T，把大于这个阈值T的部分截断。

        现在的问题是如何选取阈值T，我们先来看一下在同一批图片输入下不同网络结构的不同layer的激活值分布，有卷积层，有池化层，他们之间的分布很不一样，因此合理的量化方式应该适用于不同的激活值分布，并且减小信息损失。

        因此我们就需要一个衡量指标来衡量不同的 INT8 分布与原来的FP32分布之间的差异程度。这个衡量指标就是 相对熵（relative entropy），又称为KL散度（Kullback–Leibler divergence，简称KLD），又称相对熵。

1、相对熵

        我们先来解释以下相对熵的概念。

        相对熵表述的就是两个分布的差异程度，在我们的情境里就是量化前后两个分布的差异程度。差异越小越好，因此问题转换为求相对熵的最小值！

相对熵=交叉熵-信息熵

        其中p(i)表示一组数据的真实分布，q(i)表示另一组数据的理论分布、模型分布或p(i)的近似分布。

        回到我们的主题，我们要做的就是让q尽量接近p，也就是相对熵尽量小。

2、Calibration

        NVIDIA官方为了寻找最优T，是从验证集选取一个子集作为校准集，校准集应该具有代表性，多样性。

        NVIDIA官方的伪代码如下：

1、首先要做的是校准集上进行FP32推理，分别统计每一层的激活值并做直方图，分成几个组别（bins，官方推荐2048组）。

2、在[128,2048]范围内循环执行以下3-5步骤

3、将第i个bin后的所有数值累加到第i-1个bin上，并对前128个bins归一化，作为P分布（真实分布）

4、对P量化得到Q并归一化

5、计算P与Q的相对熵

6、得到最小相对熵的i，阈值T=（i+0.5）*bin的宽度

        这样就得到了阈值T，使用阈值T得到的截断效果如下：

         精确度比较如下：

四、用TensorRT实现Int8量化加速

         根据TensorRT的官网可以知道，整个过程分为以下四步：

         翻译过来就是：

1. 将预训练的pytorch模型转换位ONNX；
2. 将ONNX模型导入TensorRT；
3. 应用优化并生成引擎；
4. 在GPU上执行推理过程。

1、ONNX

        Open Neural Network Exchange（ONNX，开放神经网络交换）格式，是一个用于表示深度学习模型的标准，可使模型在不同框架之间进行转移。

维基百科：

         ONNX是一种针对机器学习所设计的开放式的文件格式，用于存储训练好的模型。它使得不同的人工智能框架（如Pytorch, MXNet）可以采用相同格式存储模型数据并交互。 ONNX的规范及代码主要由微软，亚马逊 ，Facebook 和 IBM 等公司共同开发，以开放源代码的方式托管在Github上。目前官方支持加载ONNX模型并进行推理的深度学习框架有： Caffe2, PyTorch, MXNet，ML.NET，TensorRT 和 Microsoft CNTK，并且 TensorFlow 也非官方的支持ONNX。

安装ONNX：

        本文基于anaconda3和pytorch，具体可以参考以下链接Anaconda及pytorch详细安装及使用教程。在anaconda prompt中依次输入以下指令即可。

# 安装指令
activate pytorch # 切换到anaconda中你创建的项目下，这里是pytorch
conda install -c conda-forge numpy protobuf==3.16.0 libprotobuf=3.16.0
conda install -c conda-forge onnx
pip install onnxruntime

# 测试是否安装成功
python
import onnx #此步后如果没有报错就说明安装成功

 将pytorch模型导出成onnx

        在Python中执行以下代码：

import torch
import torchvision

dummy_input = torch.randn(1, 3, 224, 224, device='cuda') # 仿真输入，其尺寸需要与模型匹配
model = torch.load("savepath.pth")

input_names = ["input_1"] # 输入的名字
output_names = ["output_1"] # 输出的名字
onnx_path = "H:\Lenet.proto" # ONNX模型的路径及名字

torch.onnx.export(model, dummy_input, onnx_path, verbose=True, input_names=input_names, output_names=output_names) # 使用verbose=True输出模型结构

         执行成功后在命令行会有类似如下的显示：

graph(%input_1 : Float(16:67500, 3:22500, 150:150, 150:1),
      %conv1.weight : Float(32:27, 3:9, 3:3, 3:1),
      %conv1.bias : Float(32:1),
      %conv2.weight : Float(64:288, 32:9, 3:3, 3:1),
      %conv2.bias : Float(64:1),
      %conv3.weight : Float(128:576, 64:9, 3:3, 3:1),
      %conv3.bias : Float(128:1),
      %fc1.weight : Float(512:36992, 36992:1),
      %fc1.bias : Float(512:1),
      %fc2.weight : Float(2:512, 512:1),
      %fc2.bias : Float(2:1)):
      %32 : Long(1:1)):
  %11 : Float(16:700928, 32:21904, 148:148, 148:1) = onnx::Conv[dilations=[1, 1], group=1, kernel_shape=[3, 3], pads=[0, 0, 0, 0], strides=[1, 1]](%input_1, %conv1.weight, %conv1.bias) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:415:0
  %12 : Float(16:700928, 32:21904, 148:148, 148:1) = onnx::Relu(%11) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:1119:0
  %13 : Float(16:175232, 32:5476, 74:74, 74:1) = onnx::MaxPool[kernel_shape=[2, 2], pads=[0, 0, 0, 0], strides=[2, 2]](%12) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:575:0
  %14 : Float(16:331776, 64:5184, 72:72, 72:1) = onnx::Conv[dilations=[1, 1], group=1, kernel_shape=[3, 3], pads=[0, 0, 0, 0], strides=[1, 1]](%13, %conv1.weight, %conv1.bias) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:415:0
  %15 : Float(16:331776, 64:5184, 72:72, 72:1) = onnx::Relu(%14) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:1119:0
  %16 : Float(16:82944, 64:1296, 36:36, 36:1) = onnx::MaxPool[kernel_shape=[2, 2], pads=[0, 0, 0, 0], strides=[2, 2]](%15) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:575:0
  %17 : Float(16:147968, 128:1156, 34:34, 34:1) = onnx::Conv[dilations=[1, 1], group=1, kernel_shape=[3, 3], pads=[0, 0, 0, 0], strides=[1, 1]](%16, %conv1.weight, %conv1.bias) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:415:0
  %18 : Float(16:147968, 128:1156, 34:34, 34:1) = onnx::Relu(%17) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:1119:0
  %19 : Float(16:36992, 128:289, 17:17, 17:1) = onnx::MaxPool[kernel_shape=[2, 2], pads=[0, 0, 0, 0], strides=[2, 2]](%18) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:575:0
  %20 : Tensor = onnx::Shape(%19)
  %21 : Tensor = onnx::Constant[value={0}]()
  %22 : Long() = onnx::Gather[axis=0](%20, %21) # L:\CaDModel\model\cadmodel.py:37:0
  %24 : Tensor = onnx::Unsqueeze[axes=[0]](%22)
  %26 : Tensor = onnx::Concat[axis=0](%24, %32)
  %27 : Float(16:36992, 36992:1) = onnx::Reshape(%19, %26) # L:\CaDModel\model\cadmodel.py:37:0
  %28 : Float(16:512, 521:1) = onnx::Gemm[alpha=1, beta=1, transB=1](%27, %fc1.weight, %fc1.bias) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:1674:0
  %29 : Float(16:512, 512:1) = onnx::Relu(%28) # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:1119:0
  %30 : Float(16:2, 2:1) = onnx::Gemm[alpha=1, beta=1, transB=1](%29, %fc2.weight, %fc2.bias), # C:\Users\xxx\AppData\Local\conda\conda\envs\pytorch\lib\site-packages\torch\nn\modules\conv.py:1674:0
  %output_1 : Float(16:2, 2:1) = onnx::Sigmoid(%30) # L:\CaDModel\model\cadmodel.py:43:0
  return (%output_1)

参考资料：Binary neural networks A survey

 8-bit inference with TensorRT

从TensorRT看INT8量化原理