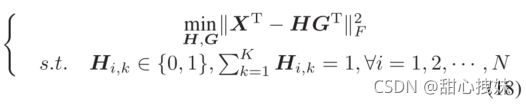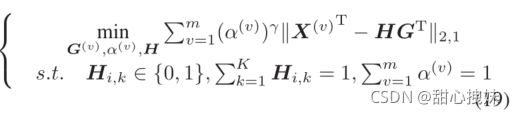多视图聚类综述

多视图聚类方法分类：

区分方法（基于相似性）的方法： 

MVC的目的是将N个主体分成K个类别，最终我们会得到一个成员矩阵H∈（N×K),它会指示哪一个主题是在同一个簇而其他主体是在其他簇。H的每一行的元素之和应该是1，这样可以确保每一行的等可能性。

A.公共向量矩阵（多视图谱聚类）

       谱聚类的关键在于图的拉普拉斯构造，得到的特征向量反映了数据的分组结构，这组MVC方法通过假设所有视图共享相同或相似的特征向量矩阵来保证得到共同的聚类结果。有两种代表性的方法：联合训练谱聚类（co-training approach for multi-view spectral clustering）和联合正则化谱聚类（“Co-regularized multi-view spectral clustering）。

1）谱聚类：利用图的拉普拉斯性质，其中图的边表示数据点之间的相似性，并解决图上归一化最小割的松弛问题。与其他广泛使用的方法（如仅适用于球形聚类的kmeans)相比，谱聚类可以应用于任意形状的聚类，并表现出良好的性能。目标函数如下：

矩阵U的行是数据点的嵌入，可以被用来当作kmeans的输入。 

关于谱聚类的具体操作可以去搜其他博客，这里只做简要介绍。

2）协同训练多视图谱聚类：对于半监督学习，当标记和未标记的数据都可用时，两个视图的联合训练是一种广泛认可的想法。它假设在两个视图中构建的预测模型将很可能导致同一样本的相同标签。有两个主要假设可以保证共同训练的成功：（1）充分性：每个视图本身足以进行样本分类，（2）条件独立性：给定类标签，视图是条件独立的。在原始联合训练算法（Combining labeled and unlabeled data with co-training）中，使用标记数据在每个视图中训练两个初始预测函数F1和F2，然后重复执行以下步骤：将F1预测的最有把握的示例添加到标记集TrainF2，反之亦然，然后在放大的标记数据集上重新训练F1和F2。可以看出，经过多次迭代后，F1和F2将在标签上彼此一致。

3）共正则化多视角谱聚类：共正则化是半监督多视图学习中的一种有效技术。协同正则化的核心思想是最小化作为目标函数一部分的两个视图的预测函数之间的差异。然而，在无监督学习类聚类中不存在预测函数，那么如何在聚类问题中实现协同正则化思想呢？联合正则化多视图谱聚类（Co-regularized multi-view spectral clustering）采用了图拉普拉斯算子的特征向量，在半监督模式下扮演类似于预测函数的角色。

     第一种共正则化方法：

这个方法在不完整多视图聚类中有用到，这篇论文：《 Incomplete Multiview Spectral Clustering With Adaptive Graph Learning》

        第二种称为基于质心的联合正则化，通过将每个视图的特征向量矩阵正则化为一个共同一致的特征向量矩阵，从而使每个视图的特征向量相似。提出了相应的优化问题：

与两两正则化算法相比，基于质心的多视图聚类算法不需要将得到的所有视图的特征向量矩阵进行组合，就可以运行kmeans算法，然而，基于质心的方法有一个潜在的缺点：噪声视图可能会影响最佳特征向量，因为它取决于所有视图。 

Cai等人（Heterogeneous image feature integration via multi-modal spectral clustering）在视图中使用公共指示矩阵来执行多视图谱聚类，并推导出类似于基于质心的共正则化方法的公式。在每一个视图的特征向量矩阵和公共特征向量矩阵之间的不一致性判别为：

优化问题定义如下：

与一般的谱聚类不同，一般谱聚类先得到特征向量矩阵，然后再运行聚类（如对初始化条件敏感的k均值）来分配聚类，cai等人直接求解最终的聚类指示矩阵，因此对初始条件更具有鲁棒性。 

4）其他： 除了上述两种具有代表性的多视图谱聚类方法外，wang等人（Multi-objective multi-view spectral clustering via pareto optimization）在视图间强制执行一个公共特征向量矩阵，并制定一个multi-objective问题，然后使用Pareto优化。

---

B.公共系数矩阵（主要是多视图子空间聚类）

在许多实际应用中，即使给定的数据是高维的，问题的内在维数往往很低。例如，给定图像中的像素数可能很大，但仅使用少数参数来描述场景的外观、几何体和动力学。这推动了寻找底层低维子空间的发展。实际上，数据可以从多个子空间中采样。子空间聚类（A tutorial on subspace clustering）是找到底层子空间，然后根据已识别的子空间正确聚类数据点的技术。

1）子空间聚类：子空间聚类使用数据样本的自表达特性[Sparse subspace clustering: Algorithm, theory, and applications,]，即，每个样本都可以由少数其他数据样本的线性组合表示。经典的子空间聚类公式如下所示：

      Z即是子空间系数矩阵（表示矩阵），可以写作以下优化问题：

在得到子空间表示Z后，可以构造出相似矩阵W，然后进一步构造出拉普拉斯矩阵，接着执行谱聚类得到最终的聚类结果。

2）多视图子空间聚类： 当有多视图信息的时候，每个视图的子空间表示Z（v)可以从每个视图中获得，Yin等人（Multi-view clustering via pairwise sparse subspace representation）通过强制每对视图的系数矩阵尽可能相似来共享公共系数矩阵，优化问题如下：

 其中是基于成对共正则化约束的l1范数，能够减轻噪声影响。

---

C.公共指示矩阵（主要是多视图非负矩阵分解） 

1）非负矩阵分解（NMF）：目的是找到两个非负的矩阵U和V，它们的积能很好地近似于X，由于非负约束，NMF的一个特性是可以学习part-based的表示。

2）基于NMF的多视图聚类：为了在NMF框架中组合多视图信息，Akata等人（Non-negative matrix factorization in multimodality data for segmentation and label prediction）在不同视图之间的NMF中强制执行一个公共指示矩阵，以执行多视图聚类。然而，指示矩阵V（v)在相同规模上可能没有可比性。为了使不同视图中的聚类解决方案保持有意义和可比性，Liu等人（Multi-view clustering via joint nonnegative matrix factorization）实施了一个约束，将每个视图相关的指示矩阵推向一个共同的指示矩阵，这导致了另一个受NMF和概率潜在语义分析之间联系启发的规范化约束，最终优化问题的公式为：

 即是保证比较的合理性约束，在获得了共识矩阵V*之后，每一个数据点的簇标签都可以通过计算出来。

3）多视图k-means：通过引入指示矩阵H，可以使用NMF来制定k-均值聚类方法。k-means聚类的NMF公式是：

 其中G∈R（d×K)的列给出簇的质心。为了处理大规模多视图数据，Cai等人（Multi-view k-means clustering on big data）提出了一种多视图kmeans聚类方法，通过在不同视图之间采用公共指示矩阵，优化问题如下：

通过学习不同视图的权重α，在多视图聚类过程中，重要视图将获得较大的权重

4）其他 ：如前所述，在子空间聚类中通常有两个步骤：找到子空间表示，然后在根据子空间表示计算出的图Laplacian上运行谱聚类。为了从不同的视图中识别一致的聚类，Gao等人[Multi-view subspace clustering]将这两个步骤合并到子空间聚类中，并在不同的视图中实施了一个通用的指标矩阵。公式如下所示：

 H是公共指示矩阵，该矩阵指示所有视图的唯一群集分配。尽管这种多视图子空间聚类方法基于子空间聚类，但它不强制使用公共系数矩阵Z，而是为不同的视图使用公共指示矩阵。因此，我们将其归类为这一类。

 Wang等人[Multi-view clustering and feature learning via structured sparsity]通过一个公共指标矩阵集成多视图信息，并通过以下公式为不同的数据集群同时选择特征：

 在[Double constrained nmf for partial multi-view clustering]中，采用了矩阵分解方法来协调各个视图产生的聚类。具体地说，创建一个包含每个单独视图的分区指示的矩阵，然后将其分解为两个矩阵：一个显示单个groupings对最终多视图集群的贡献，称为元集群，另一个显示实例对元集群的分配。Tang等人[Clustering with multiple graphs]将多视图聚类视为具有多个图的聚类，每个图通过两个因子的矩阵分解进行近似：一个特定于图的因子和一个所有图共有的因子。Qian等人[Double constrained nmf for partial multi-view clustering]要求每个视图的指示矩阵尽可能接近公共指示矩阵，并采用拉普拉斯正则化来同时保持视图的潜在几何结构。

除了使用通用指示矩阵外，[Multiple incomplete views clustering via weighted nonnegative matrix factorization with l21 regularization]、[Weighted multi-view clustering with feature selection]、[Online multi-view clustering with incomplete views]还引入了一个权重矩阵来指示是否存在缺失条目，以便它能够解决缺失值问题。多视图自定步长聚类方法[Multi-view self-paced learning for clustering]考虑了样本和视图的复杂性，以缓解局部极小值问题。Tao等人[From ensemble clustering to multi-view clustering]实施了一个公共指标矩阵，并以集成的方式在所有视图中寻求共识聚类。另一种利用公共指标矩阵组合多个视图的方法[Discriminatively embedded k-means for multi-view clustering]采用了线性判别分析思想，并自动对不同视图进行加权。对于基于图形的聚类方法，首先获得每个视图的相似性矩阵，Nie等人[Self-weighted multiview clustering with multiple graphs]假设一个公共指标矩阵，然后通过最小化公共指标矩阵和每个相似性矩阵之间的差异来解决问题。

D.直接组合（主要是基于多内核的多视图聚类）：除了在不同视图之间共享某些结构的方法外，通过内核进行直接视图组合是执行多视图聚类的另一种常见方法。一种自然的方法是为每个视图定义一个内核，然后将这些内核组合成凸组合[Composite kernels for hypertext categorisation][Linear prediction models with graph regularization for web-page categorization][Multi-kernel maximum entropy discrimination for multi-view learning]

因为我对这块不是很感兴趣，所以只做列举

1）核函数和核组合方法：

组合多个内核的方法：

2）核kmeans和谱聚类： 

 3）基于多核的多视图聚类

4）其他：除了基于多内核的多视图聚类外，还有一些其他方法使用特征的直接组合来执行多视图聚类，如[Discriminatively embedded k-means for multi-view clustering]，[Fusion of similarity data in clustering]。在[Tw-k-means: Automated two-level variable weighting clustering algorithm for multiview data]中，为多视图数据的聚类算法分配了两级权重：视图权重和变量权重，以确定相应视图和变量的重要性。为了将模糊聚类方法扩展到多视图聚类，在[Cofkm: a centralized method for multiple-view clustering]和[Optimized data fusion for kernel k-means clustering]中分别对每个视图进行加权，并获得模糊c-均值和模糊k-均值的多视图版本。

---

 E.投影后的组合（主要是基于CCA的多视图聚类）：

 对于所有视图都具有相同数据类型（如“分类”或“连续”）的多视图数据，直接将它们组合在一起是合理的。然而，在实际应用中，多个表示可能具有不同的数据类型，很难直接比较它们。例如，在生物信息学中，基因信息可以是一个视图，而临床症状可以是患者聚类分析的另一个视图[Multi-view sparse co-clustering via proximal alternating linearized minimization]。显然，这些信息不能直接组合。此外，高维度和噪声也很难处理。为了解决上述问题，介绍了最后一种重要的组合方式：投影后组合。最常用的技术是典型相关分析（CCA）和核心版本的CCA（KCCA）。

1）CCA和KCCA

2）基于CCA的多视图聚类

 对于至少有一个完整视图的多视图数据（该视图的特征可用于所有数据点），Anusua等人[Muliview clusterting with incomplete views]借用了拉普拉斯正则化的思想来完成不完整的核矩阵，然后应用KCCA进行多视图聚类。在多视图聚类的另一种方法中，多模式矩阵A（v）∈R（N×Kv），v=1,2，···，其中每一个K对应于一个视图，然后应学习一致模式矩阵以尽可能逼近每个视图的模式矩阵。然而，由于无监督的特性，模式矩阵通常不能直接进行比较。使用CCA公式（29），Long等人[A general model for multiple view unsupervised learning]首先投影一个视图的模式矩阵，然后再与另一个视图的模式矩阵进行比较。

 同样的想法也可以用来解决不完整视图问题（即，没有完整视图）。例如，如果只有两个视图，[Partial multi-view clustering]、[Incomplete multi-view clustering via subspace learning]中的方法将数据分成两个视图的数据部分和只有一个视图的数据部分，然后投影每个视图的数据矩阵，使其接近最终指示矩阵。多视图信息由公共指示矩阵连接，该矩阵对应于两个视图的投影数据。Wang等人[Multi-view clustering with extreme learning machine]提供了一种使用极限学习机的多视图聚类方法，该方法将归一化特征空间映射到更高维的特征空间。