【面经专栏】自己整理的数据结构与算法面经

1、排序算法的稳定性

堆排序、快速排序是不稳定的排序算法，而冒泡排序、插入排序、归并排序是稳定的排序算法。

​ 【总结排序算法实现与稳定性】https://www.cnblogs.com/lqminn/p/3642027.html

​ 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原 序列中，ri=rj，且ri在rj之前，而在排序后的序列中，ri仍在rj之前，则称这种排序算法是稳定的；否则称为不稳定的。

2、红黑树和AVL树的区别

AVL树是带有平衡条件的二叉查找树，一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡，左右子树树高不超过1，和红黑树相比，AVL树是严格的平衡二叉树，平衡条件必须满足（所有节点的左右子树高度差的绝对值不超过1）。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的，由此我们可以知道AVL树适合用于插入与删除次数比较少，但查找多的情况

一种二叉查找树，在每个节点增加一个存储位表示节点的颜色，可以是红或黑（非红即黑）。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制，红黑树确保没有一条路径会比其它路径长出两倍，因此，红黑树是一种弱平衡二叉树（由于是弱平衡，可以看到，在相同的节点情况下，AVL树的高度低于红黑树），相对于要求严格的AVL树来说，它的旋转次数少，所以对于搜索，插入，删除操作较多的情况下，我们就用红黑树。

红黑树有如下特征：

1. 每个节点非红即黑
2. 根节点是黑的
3. 每个叶节点（叶节点即树尾端NULL指针或NULL节点）都是黑的
4. 如果一个节点是红的，那么它的两儿子都是黑的
5. 对于任意节点而言，其到叶子点树NULL指针的每条路径都包含相同数目的黑节点

红黑树的应用：

1. STL的map和set
2. IO多路复用的epoll的的的实现采用红黑树组织管理的的的sockfd，以支持快速的增删改查
3. Linux用红黑树管理进程控制块，进程的虚拟内存区域都存储在一颗红黑树上，每个虚拟地址区域都对应红黑树的一个节点

3、最快的排序算法

在平均情况下，快速排序最快；
在最好情况下，插入排序和冒泡排序最快；
在最坏情况下，堆排序和归并排序最快

4、hash表排序，对应的优化

#include 
#include 

int main(int argc, char const *argv[])
{
    int random[10] = {999, 1, 444, 7, 20, 9, 1, 3, 7, 7};
    int hash_map[1000] = {0};//这里规定为1000足以容得下所有数据范围，一般取random数组中出现的数值范围
    // 开始排序
    for(int i = 0; i < 10; i++) {
        hash_map[random[i]]++;
    }
    // 打印排序结果
    for(int i = 0; i < 1000; i++) {
        /* code */
        for(int j = 0; j < hash_map[i]; j++) {
            printf("%d\n", i);
        }
    }
    
    return 0;
}

将待排序数组nums中的数存放到哈希表中，nums[i]存到下标为哈希表hash_map的下标nums[i]处，hash_map[nums[i]]的值即nums[i]在nums中的出现次数

最后，从前向后遍历hash_map，输出不为0的值（若hash_map[nums[i]]>1，则在该位置上循环输出所有的nums[i]）

时间复杂度 O(m*n)，m为nums数组长度，n为nums[i]的重复次数

5、二叉树的前序遍历、层序遍历时间复杂度

前中后序遍历采用递归与迭代的方式，每个节点均访问一次，时间复杂度是O(n)

递归的方式要是用栈空间，空间复杂度也是O(n)

6、快速排序、归并排序的时间复杂度怎么计算的

快排：最好O(nlogn)，平均O(nlogn)，最坏O(n²)

每次分成两段，那么分的次数就是logn了，每一次处理需要n次计算，那么时间复杂度就是nlogn。注意这是平均时间复杂度，但是在分的时候可能并不均匀。最坏是O(n^2)，这种情况就是数组刚好是有序，然后每次取pivot的时候都是取最大或者最小

最优的情况下空间复杂度为：O(logn) ；每一次都平分数组的情况

最差的情况下空间复杂度为：O( n ) ；退化为冒泡排序的情况

归并：最好O(nlogn)，平均O(nlogn)，最差O(nlogn)

因为采用分治，先分成最小的两段，在“治”的过程中再merge，这样不管什么情况，始终是O(nlogn)

7、对于一个排序算法，哪方面是最重要的

一个排序算法的好坏，取决于时间复杂度、空间复杂度、使用场景和稳定性

稳定性是一个特别重要的评估标准。稳定的算法在排序的过程中不会改变元素彼此的位置的相对次序，反之不稳定的排序算法经常会改变这个次序。我们在使用排序算法或者选择排序算法时，更希望这个次序不会改变，更加稳定，所以排序算法的稳定性，是一个特别重要的参数衡量指标依据。

8、完全二叉树、二叉搜索树、平衡二叉树、红黑树、B树、B+树

完全二叉树：

若设二叉树的深度为k，除第 k 层外，其它各层 (1～k-1) 的结点数都达到最大个数，第k 层所有的结点都连续集中在最左边，这就是完全二叉树。

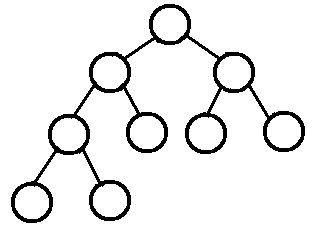
二叉查找树：

左子树的节点都小于根节点，右子树的节点都大于根节点

**平衡二叉树：**时间复杂度：查找O(logn)、插入删除O(logn)，在每一偶次增删节点后，可能会出现旋转操作

是二叉查找树的一个进化体，又叫AVL树。平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态

这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

红黑树就是一种弱平衡二叉树，时间复杂度：查找O(logn)、插入删除O(logn)

由于红黑树的弱平衡，它查询的时间复杂度在同等级别上略高于平衡二叉树，适用于增删频繁的场景

B树：

B 树相对于平衡二叉树，每个节点存储了更多的键值（key）和数据（data），并且每个节点拥有更多的子节点。基于这个特性，B 树查找数据读取磁盘的次数将会很少，数据的查找效率也会比平衡二叉树高很多。

B+树：

B+ 树是对 B 树的进一步优化。

1. B+ 树非叶子节点上是不存储数据的，仅存储键值，而 B 树节点中不仅存储键值，也会存储数据

   如果不存储数据，那么就会存储更多的键值，相应的树的阶数（节点的子节点树）就会更大，树就会更矮更胖，如此一来我们查找数据进行磁盘的 IO 次数又会再次减少，数据查询的效率也会更快。

2. B+树所有数据均存放于叶子节点，查找任意一个数据均需要从根节点走到叶子节点，使得查询效率更加稳定

3. B+树叶子节点连接成链表，支持范围查询，B树只能使用中序遍历按序扫库

9、红黑树怎么确定节点颜色

根据红黑树的性质：

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的 ( 此处的叶子结点指的是空结点 )

插入红色节点树的性质可能不会改变，而插入黑色节点每次都会违反性质4.

通过性质发现： 将节点设置为红色在插入时对红黑树造成的影响是小的，而黑色是最大的

将红黑树的节点默认颜色设置为红色，是为尽可能减少在插入新节点对红黑树造成的影响

10、冒泡排序的优化

1. 优化1：在交换的地方加一个标记，如果那一趟排序没有交换元素，说明这组数据已经有序，不用再继续下去。
2. 优化2：记下最后一次交换的位置，后边没有交换，必然是有序的，然后下一次排序从第一个比较到上次记录的位置结束即可
3. 优化3：一次排序可以确定两个值，正向扫描找到最大值交换到最后，反向扫描找到最小值交换到最前面

https://blog.csdn.net/hansionz/article/details/80822494?utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control

12、哈希是无序的，怎样保证插入删除的顺序

LRU

双向链表、插入删除查看的时候将目标节点移动到链表头部

13、M个苹果放在N个盘子里，有多少种不同的放法

https://blog.csdn.net/wengyupeng/article/details/84753175?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.essearch_pc_relevant&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.essearch_pc_relevant

14.冒泡排序、快速排序的适用场景

冒泡：适用于数据量很小的排序场景，因为冒泡原理简单

快排：适用于数据杂乱无章的场景，而且越乱，快速排序的效率越体现的淋漓尽致

15、从两个文件（50亿记录）中找到共同的记录

给定a、b两个文件，各存放50亿个url，每个url各占用64字节，内存限制是4G，如何找出a、b文件共同的url？

• 可以估计每个文件的大小为5G*64=300G，远大于4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。
  1. 遍历文件a，对每个url求取hash(url)%1000，然后根据所得值将url分别存储到1000个小文件（设为a0,a1,…a999）当中。这样每个小文件的大小约为300M。遍历文件b，采取和a相同的方法将url分别存储到1000个小文件(b0,b1….b999)中。这样处理后，所有可能相同的url都在对应的小文件(a0 vs b0, a1 vs b1….a999 vs b999)当中，不对应的小文件（比如a0 vs b99）不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。
  2. 比如对于a0 vs b0，我们可以遍历a0，将其中的url存储到hash_map当中。然后遍历b0，如果url在hash_map中，则说明此url在a和b中同时存在，保存到文件中即可。
  3. 如果分成的小文件不均匀，导致有些小文件太大（比如大于2G），可以考虑将这些太大的小文件再按类似的方法分成小小文件即可。

16、从1亿个数里面找出前100个最大的

先hash去重，如果文件还是很大就分成小文件，对每一个小文件采用最小堆排序，最后所有小文件的堆中元素来排序

17、有23枚硬币在桌上，10枚正面朝上。蒙住你的眼睛，如何让左右两摞硬币正面朝上的一样多

https://blog.csdn.net/leingz/article/details/17171037

18、如何用5L和6L的杯子，得到3L的水

https://zhidao.baidu.com/question/653421752315561725.html

19、从100亿条记录的文本文件中取出重复数最多的前10条

https://blog.csdn.net/qq_26498709/article/details/78432054

1. 先设计一个哈希函数，把100个G的文件分成10000份，每份大约是 10MB，可以加载进内存了
2. 10MB 的小文件加进内存，统计出现次数最多的那个ip（10MB 的小文件里面存着很多 ip，他们虽然是乱序的，但是相同的 ip 会映射到同一个文件中）
3. 用map存（ip, count），排序规则为count降序
4. 读每个小文件的map中前10个ip，比较所有小文件的前10个ip

20、LRU的优缺点

https://www.jianshu.com/p/213ea9000e1a

1.**命中率,**当存在热点数据时,LRU的效率很好,但偶发性的,周期性的批量操作会导致LRU命中率急剧下降,缓存污染情况比较严重

2,实现相对简单

3,命中时需要遍历链表,找到命中的数据块索引,然后需要将数据移到头部

21、判断一棵树是否为完全二叉树

https://blog.csdn.net/qq_37236745/article/details/107077078