SVM(一):SVM入门
SVM简介
支持向量机SVM(support vector machines)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器。间隔最大使它有别于感知机。SVM还包括核技巧,这使它成为实际上的非线性分类器。SVM的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。
SVM的的学习算法就是求解凸二次规划的最优化算法。
SVM相关定义
1、分离超平面
w ⋅ x + b = 0 w·x+b=0 w⋅x+b=0
分离超平面由法向量w和截距b决定,可用(w,b)表示。分离超平面将特征空间划分为正类、负类两部分。法向量指向的一侧为正类,另一侧为负类。
2、分离决策函数
f ( x ) = s i g n ( w ∗ ⋅ x + b ∗ ) f(x)=sign(w^*·x+b^*) f(x)=sign(w∗⋅x+b∗)
式中sign又叫sgn,是符号函数,用来提取一个数字的符号。此处用来提取出来1或者-1,分别对应正例和反例。
3、函数间隔
对于给定的训练数据集T和超平面(w,b),定义超平面(w,b)关于样本点(xi,yi)的函数间隔为:
γ ^ i = y i ( w ⋅ x i + b ) \hatγ_i=y_i(w·x_i+b) γ^i=yi(w⋅xi+b)
y(w·x+b)来表示分类的正确性及确信度,这就是函数间隔(function margin)。
定义超平面(w,b)关于训练数据集T的函数间隔为超平面(w,b)关于T中所有样本点(xi,yi)的函数间隔之最小值,即:
γ ^ = min i = 1 , ⋅ ⋅ ⋅ , N γ ^ i \hatγ=\min\limits_{i=1,···,N}\ \hatγ_i γ^=i=1,⋅⋅⋅,Nmin γ^i
4、几何间隔
函数间隔可以表示分类预测的正确性及确信度。但是选择分离超平面时,只有函数间隔还不够,因为只要成比例地改变w和b,例如将它们改为2w和2b,超平面并没有改变,但函数间隔却成为原来的2倍。
因此我们需要对超平面的法向量加以约束,如令||w||=1,使得间隔是确定的。此时函数间隔成为几何间隔(geometric margin)。
给出超平面(w,b)和其法向量w。点A表示某一实例xi,其类标记为yi=±1。点A与超平面(w,b)的距离由线段AB给出,记作γi。
(1)如果A在超平面正的一侧,即yi=+1,点与超平面的距离:
γ i = w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ γ_i = \frac{w}{||w||}·x_i + \frac{b}{||w||} γi=∣∣w∣∣w⋅xi+∣∣w∣∣b
(2)如果A在超平面负的一侧,因为距离是正的,而括号内得出的结果是负的。yi=-1,点与超平面的距离:
γ i = − ( w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ ) γ_i =-( \frac{w}{||w||}·x_i + \frac{b}{||w||} ) γi=−(∣∣w∣∣w⋅xi+∣∣w∣∣b)
(3)一般地,当样本点(xi,yi)与超平面(w,b)正确分类时,点xi与超平面(w,b)的距离:
γ i = y i ( w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ ) γ_i =y_i( \frac{w}{||w||}·x_i + \frac{b}{||w||} ) γi=yi(∣∣w∣∣w⋅xi+∣∣w∣∣b)
与函数间隔类似,训练数据集T与超平面(w,b)的间隔为所有点到超平面的几何间隔的最小值,即:
γ = min i = 1 , ⋅ ⋅ ⋅ , N γ i γ=\min\limits_{i=1,···,N}\ γ_i γ=i=1,⋅⋅⋅,Nmin γi网页链接:函数间隔到几何间隔的推导过程
从上面可以看出函数间隔和几何间隔有下面的关系:
γ = γ ^ ∣ ∣ w ∣ ∣ γ = \frac{\hat γ}{||w||} γ=∣∣w∣∣γ^
从上面的高亮字体中我们了解到w和b同比例变化时导致的函数间隔的改变对超平面是没有影响的,因此我们令 γ ^ = 1 \hat γ=1 γ^=1,带入上式得到 γ = 1 ∣ ∣ w ∣ ∣ γ=\frac{1}{||w||} γ=∣∣w∣∣1。又因 γ ^ = 1 ∣ ∣ w ∣ ∣ \hat γ=\frac{1}{||w||} γ^=∣∣w∣∣1的最大化和 γ = 1 2 ∣ ∣ w ∣ ∣ 2 γ=\frac{1}{2}||w||^2 γ=21∣∣w∣∣2的最小化是相同的,因此就得到了下面线性可分支持向量机学习的最优化问题:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min\limits_{w,b} \frac{1}{2}||w||^2 w,bmin21∣∣w∣∣2
s . t . y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , 2 , … , N s.t. \ \ \ \ y_i(w·x_i+b)-1≥0,i=1,2,…,N s.t. yi(w⋅xi+b)−1≥0,i=1,2,…,N
5、支持向量和间隔边界
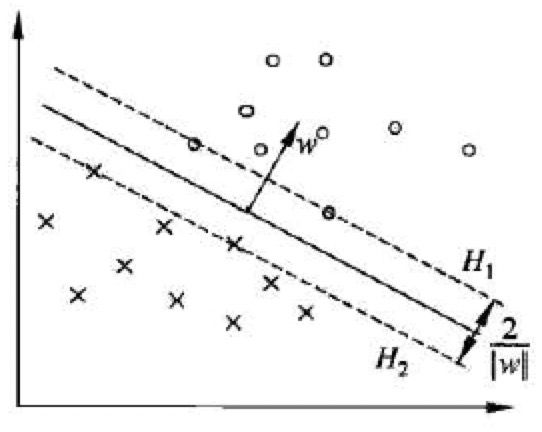
(1)在线性可分的情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例成为支持向量(support vector),支持向量是使上面约束条件式等号成立的点。在上图中,落在H1和H2上面的点即为支持向量。
(2)我们可以看到H1和H2是平行的,没有实例点落在他们中间。H1和H2之间的距离称为间隔(margin),间隔依赖于分离超平面的法向量w,等于 2 ∣ ∣ w ∣ ∣ \frac{2}{||w||} ∣∣w∣∣2,H1和H2称为间隔边界。
6、支持向量机
由于支持向量在确定分离超平面中起着决定性作用,所以将这种分类模型称为支持向量机。支持向量的个数一般很少,所以支持向量机由很少的“重要的”训练样本确定。
支持向量机由简至繁包括三种:
(1)线性可分支持向量机Linear support vector machine in linearly separable case
(2)线性支持向量机Linear support vector machine
(3)非线性支持向量机Non-Linear support vector machine
上面我们介绍的就是第一种最简单的情况。
线性可分支持向量机举例
如下图所示的训练数据集,其正例点是x1=(3,3)T,x2=(4,3)T,x3=(1,1)T,试求最大间隔分离超平面。
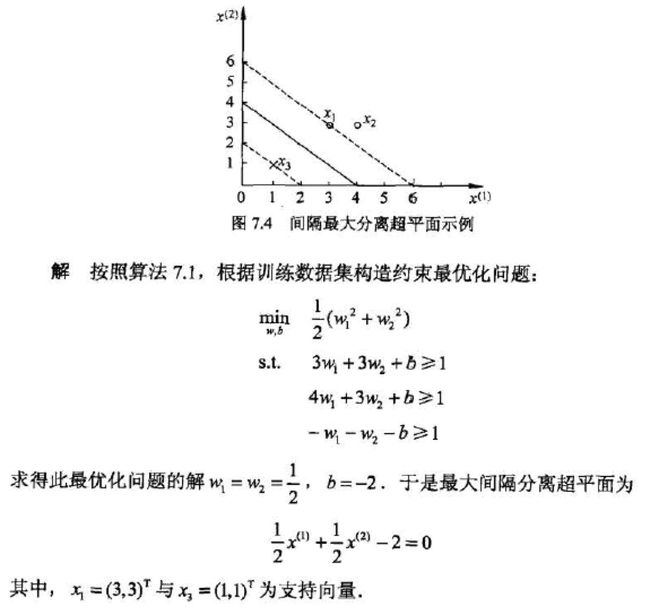
可能刚看到答案有点懵,公式是 m i n 1 2 ∣ ∣ w ∣ ∣ 2 min \frac{1}{2}||w||^2 min21∣∣w∣∣2为什么会有w1和w2两个w。注意看坐标系,横坐标为x(1),纵坐标为x(2),每个x对应一个w,因此构造出的公式为 min w , b 1 2 ( w 1 2 + w 2 2 ) \min \limits_{w,b}\ \frac{1}{2}(w_1^2+w_2^2) w,bmin 21(w12+w22)。至于这个最优化问题的解是怎么求的,画个图就很清晰了。
SVM(二):对偶算法、SMO算法
函数间隔到几何间隔的推导过程