K-近邻算法全面解析
1 K-近邻算法简介
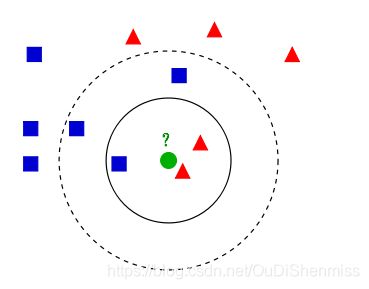
K-近邻(K-Nearest Neighbor,KNN),采用的是测量不同特征值之间距离的方法进行分类。对当前待分类样本的分类,需要大量已知分类的样本的支持,因此KNN是一种有监督学习算法。

2 K-近邻算法的三要素
2.1 样本间距离的计算方法:
既然要找到待分类样本在当前样本数据集中与自己距离最近的K个邻居,必然就要确定样本间的距离计算方法。样本间距离的计算方法的构建,与样本的向量表示方法有关,当建立样本的向量表示方法时,必须考虑其是否便于样本间距离的计算。
设特征空间 X \mathcal{X} X 是 n n n 维实数向量空间 R n , x i , x j ∈ X , x i = ( x i ( 1 ) , x i ( 2 ) , ⋯ , x i ( n ) ) T , \mathbf{R}^{n}, x_{i}, x_{j} \in \mathcal{X}, \quad x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \cdots, x_{i}^{(n)}\right)^{\mathrm{T}}, Rn,xi,xj∈X,xi=(xi(1),xi(2),⋯,xi(n))T,
x j = ( x j ( 1 ) , x j ( 2 ) , ⋯ , x j ( n ) ) T , x i , x j x_{j}=\left(x_{j}^{(1)}, x_{j}^{(2)}, \cdots, x_{j}^{(n)}\right)^{\mathrm{T}}, \quad x_{i}, x_{j} xj=(xj(1),xj(2),⋯,xj(n))T,xi,xj 的 L p L_{p} Lp 距离定义为
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( i ) − x j ( l ) ∣ p ) 1 p L_{p}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(i)}-x_{j}^{(l)}\right|^{p}\right)^{\frac{1}{p}} Lp(xi,xj)=(l=1∑n∣∣∣xi(i)−xj(l)∣∣∣p)p1
这里 p ⩾ 1. p \geqslant 1 . p⩾1. 当 p = 2 p=2 p=2 时,称为欧氏距离(Euclidean distance),即
L 2 ( x i , x j ) = ( ∑ i = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_{2}\left(x_{i}, x_{j}\right)=\left(\sum_{i=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{2}\right)^{\frac{1}{2}} L2(xi,xj)=(i=1∑n∣∣∣xi(l)−xj(l)∣∣∣2)21
当 p = 1 p=1 p=1 时,称为曼哈顿距离(Manhattan distance), 即
L 1 ( x i , x j ) = ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ L_{1}\left(x_{i}, x_{j}\right)=\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right| L1(xi,xj)=l=1∑n∣∣∣xi(l)−xj(l)∣∣∣
当 p = ∞ p=\infty p=∞ 时,它是各个坐标距离的最大值, 为切比雪夫距离“chebyshev”,即
L ∞ ( x i , x j ) = max l ∣ x i ( l ) − x j ( t ) ∣ L_{\infty}\left(x_{i}, x_{j}\right)=\max _{l}\left|x_{i}^{(l)}-x_{j}^{(t)}\right| L∞(xi,xj)=lmax∣∣∣xi(l)−xj(t)∣∣∣
K近邻算法默认的是欧式距离(即p=2的闵可夫斯基距离),我们也一般都用欧式距离来衡量高维空间中俩点的距离。
带权重闵可夫斯基距离 “wminkowski”
L p ( x i , x j ) = ( ∑ l = 1 n ( w ∗ ∣ x i ( i ) − x j ( l ) ∣ ) p ) 1 p L_{p}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}(w*\left|x_{i}^{(i)}-x_{j}^{(l)}\right|)^{p}\right)^{\frac{1}{p}} Lp(xi,xj)=(l=1∑n(w∗∣∣∣xi(i)−xj(l)∣∣∣)p)p1
汉明距离 "Hamming Distance"
在信息理论中,Hamming Distance 表示两个等长字符串在对应位置上不同字符的数目,我们以d(x, y)表示字符串x和y之间的汉明距离。从另外一个方面看,汉明距离度量了通过替换字符的方式将字符串x变成y所需要的最小的替换次数。
“karolin” and “kerstin” is 3.
1011101 and 1001001 is 2.
2.2 K值的选取
- 如果我们选取较小的k值,那么就会意味着我们的整体模型会变得复杂,容易发生过拟合。所谓的过拟合就是在训练集上准确率非常高,而在测试集上准确率低。K太小会导致过拟合,很容易将一些噪声学习到模型中,而忽略了数据真实的分布!
- 如果我们选取较大的K值,就相当于用较大邻域中的训练数据进行预测,这时与输入实例较远的(不相似)训练实例也会对预测起作用,使预测发生错误,K值的增大意味着整体模型变得简单。
- K值既不能过大,也不能过小。那么我们一般怎么选取呢?李航博士的书上讲到,我们一般选取一个较小的数值,通常采取交叉验证法来选取最优的K值。
2.3 特征归一化的重要性
首先举例如下,用一个人身高(cm)与脚码(尺码)大小来作为特征值,类别为男性或者女性。我们现在如果有5个训练样本,分布如下:
A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]
通过上述训练样本,看出问题了吗?
很容易看到第一维身高特征是第二维脚码特征的4倍左右,那么在进行距离度量的时候,我们就会偏向于第一维特征。这样造成俩个特征并不是等价重要的,最终可能会导致距离计算错误,从而导致预测错误。
归一化和标准化的区别:
归一化:缩放仅仅跟最大、最小值的差别有关,输出范围在0-1之间。
标准化:缩放和每个点都有关系,通过方差(variance)体现出来。与归一化对比,标准化中所有数据点都有贡献(通过均值和标准差造成影响)。输出范围是负无穷到正无穷。

什么时候用归一化?什么时候用标准化
- 如果对输出结果范围有要求,用归一化
- 如果数据较为稳定,不存在极端的最大最小值,用归一化
- 如果数据存在异常值和较多噪音,用标准化,可以间接通过中心化避免异常值和极端值的影响
2.4 分类决策规则
K近邻算法的分类决策规则通俗来说就是K近邻法中的分类决策规则往往是多数表决决定,背后的数学思维是什么?
K近邻法中的分类决策规则往往是多数表决,即由输入实例的K个近邻的训练实例中的多数类决定输入实例的类。多数表决规则,等价于经验风险最小化。
3 K-近邻算法优缺点分析
-
优点
(1)K-近邻算法是分类数据最简单最有效的算法,它是一种lazy-learning算法;
(2)分类器不需要使用训练集进行训练,训练时间复杂度为0;
(3)对异常值不敏感(个别噪音数据对结果的影响不是很大);
(4)适合于多分类问题(multi-modal,对象具有多个类别标签),KNN要比SVM表现要好。 -
缺点
(1)计算复杂度高、空间复杂度高:KNN分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为n,那么KNN的分类时间复杂度为O(n);
(2)耗内存:必须保存全部的数据集,如果训练数据集很大,必须使用大量的存储空间;
(3)耗时间:必须对数据集中的每一个数据计算距离值,实际使用时可能非常耗时;
(4)无法给出任何数据的基础结构信息(数据的内在含义),这是k-近邻算法最大的缺点。可解释性差,无法告诉你哪个变量更重要,无法给出决策树那样的规则。
4 K-近邻算法的问题及解决方案
问题1:当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的k个邻居中大容量类的样本占多数。
解决:不同样本给予不同的权重项
问题2:数字差值最大的属性对计算结果的影响最大
解决:在处理不同取值范围的特征值时,通常采用的方法是将数值归一化,如将取值范围处理为0到1或者-1到1之间。
5 K-近邻算法的代码实现
5.1 scikit-learn 中KNN相关的类库概述
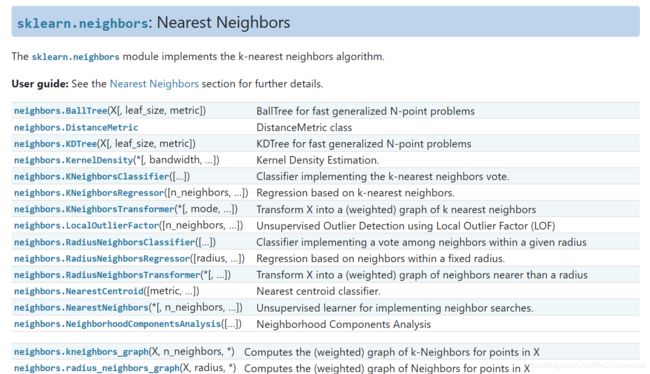
在scikit-learn 中,与近邻法这一大类相关的类库都在sklearn.neighbors包之中。KNN分类树的类是KNeighborsClassifier,KNN回归树的类是KNeighborsRegressor。除此之外,还有KNN的扩展,即限定半径最近邻分类树的类RadiusNeighborsClassifier和限定半径最近邻回归树的类RadiusNeighborsRegressor, 以及最近质心分类算法NearestCentroid。
在这些算法中,KNN分类和回归的类参数完全一样。限定半径最近邻法分类和回归的类的主要参数也和KNN基本一样。
比较特别是的最近质心分类算法,由于它是直接选择最近质心来分类,所以仅有两个参数,距离度量和特征选择距离阈值,比较简单,因此后面就不再专门讲述最近质心分类算法的参数。
另外几个在sklearn.neighbors包中但不是做分类回归预测的类也值得关注。kneighbors_graph类返回用KNN时和每个样本最近的K个训练集样本的位置。radius_neighbors_graph返回用限定半径最近邻法时和每个样本在限定半径内的训练集样本的位置。NearestNeighbors是个大杂烩,它即可以返回用KNN时和每个样本最近的K个训练集样本的位置,也可以返回用限定半径最近邻法时和每个样本最近的训练集样本的位置,常常用在聚类模型中。
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights=‘uniform’, algorithm=‘auto’, leaf_size=30, p=2, metric=‘minkowski’, metric_params=None, n_jobs=None, **kwargs)
参数说明:
n_neighbors: 选择最邻近点的数目k,默认为5。
weights: 邻近点的计算权重值,uniform代表各个点权重值相等;‘distance’表示与距离成反比;还可以自定义权重函数。
algorithm: 寻找最邻近点使用的算法,‘auto’,‘ball_tree’, ‘kd_tree’, ‘brute’可选,默认为‘auto。
leaf_size: 传递给BallTree或kdTree的叶子大小,这会影响构造和查询的速度,以及存储树所需的内存。
p: Minkowski度量的指数参数。p = 1 代表使用曼哈顿距离 (l1),p = 2 代表使用欧几里得距离(l2),
metric: 距离度量,点之间距离的计算方法,默认为‘minkowski’。
metric_params: 额外的关键字度量函数。
n_jobs: 为邻近点搜索运行的并行作业数。
5.2 KNN实现鸢尾花分类
Iris Data Set(鸢尾属植物数据集)是历史比较悠久的数据集,它首次出现在著名的英国统计学家和生物学家Ronald Fisher 1936年的论文《The use of multiple measurements in taxonomic problems》中,被用来介绍线性判别式分析。在这个数据集中,包括了三类不同的鸢尾属植物:Iris Setosa,Iris Versicolour,Iris Virginica。每类收集了50个样本,因此这个数据集一共包含了150个样本。
该数据集测量了所有150个样本的4个特征,分别是:sepal length(花萼长度)、sepal width(花萼宽度)、petal length(花瓣长度)、petal width(花瓣宽度),以上四个特征的单位都是厘米。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
import numpy as np
# load data
data = load_iris()
X = data['data']
Y = data['target']
# split arrays or matrices into random train and test subsets
X_train, X_test, Y_train, Y_test= train_test_split(X, Y, test_size=0.2, random_state=0)
# model train
model = KNeighborsClassifier(n_neighbors=2)
model.fit(X_train, Y_train)
# model predict
Y_pred= model.predict(X_test)
# model evaluation
correct_pred = np.count_nonzero(Y_pred==Y_test)
accuracy = correct_pred / len(Y_test)
print("model accuracy is " + str(accuracy))
# print(accuracy_score(Y_test, Y_pred))参考资料
k-近邻算法的原理和代码实现
一文搞懂k近邻(k-NN)算法