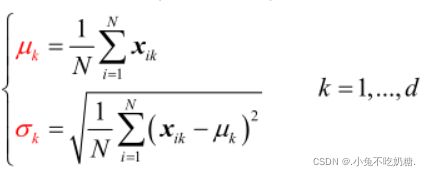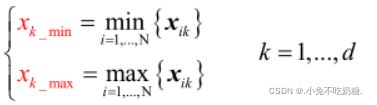大数据与人工智能方向基础 ----- K近邻分类模型

目录

前言

一、分类问题的一般描述

二、K近邻分类算法的描述

三、K近邻分类的三个基本要素

3.1 距离向量

        3.1.1 典型的距离向量方式

         3.1.2 用于距离向量的样本的标准化预处理

3.2 超参数K值

3.2.1 对超参数K值进行选择的意义

 3.2.2 基于m-fold cross validation的K值选择

3.3 决策规则

3.3.1  多数表决（胜者为王）

3.3.2  基于距离的加权投票

四、K近邻算法的实现 ---- kd树

4.1  kd树的构建(CreateKDTree)

4.2 kd树的搜索

---

前言

有很多新手刚刚接触大数据与人工智能方向学习，如果不知道怎么着手的，跟我一起慢慢进步叭~

---

提示：以下是本篇文章正文内容，下面案例可供参考

关键词：分类问题的定义，KNN分类模型，距离度量，超参数，交叉验证，性能评价

一、分类问题的一般描述

基于上述样本集，设计分类模型 ---- 分类模型的监督式学习，对特征空间的任意观测x进行类别决策 ----- 模型的使用。

二、K近邻分类算法的描述

K近邻算法没有训练过程，懒惰算法。

输入：①训练样本集D，

 ②观测样本x

输出：观测样本x所属的类别y

STEP0.训练集D的输入部分预处理，并记录预处理的使用参数

STEP1.指定距离向量，并选择K值

STEP2.训练集D内找到预处理的样本x的前k个近邻，记为

             

 STEP3.结合指定的分类规则，对x的类别y进行预测：

             其中，

在给定训练集的前提下，样本是否预处理、不同距离向量方式、不同K值、不同的决策规则，均会导致不同的分类结果。

三、K近邻分类的三个基本要素

K近邻分类的三个基本要素：距离向量，超参数K值，决策规则

3.1 距离向量

        3.1.1 典型的距离向量方式

         3.1.2 用于距离向量的样本的标准化预处理

方式一：0均值、1方差的标准化预处理（推荐使用）

首先，利用训练集估计

 然后，任意观测样本的预处理

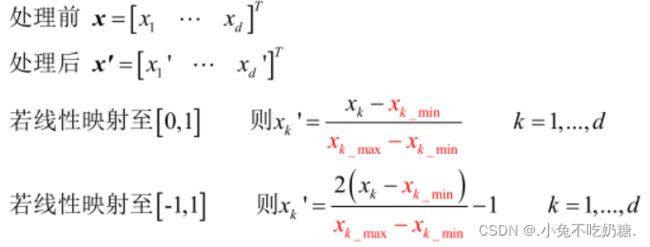
 方式二：将原始样本特征取值进行线性映射

首先，利用训练集确定

 然后，任意观测样本x的预处理

3.2 超参数K值

3.2.1 对超参数K值进行选择的意义

任意观测X的类别预测：（1）若使用较小的K值，则利用x较小邻域训练样本进行类别预测，只有更接近x的训练样本才对预测结果有作用，预测结果对近邻的训练样本类别更为敏感。若数据分布复杂或噪声影响严重，易导致高的预测错误率。最小K=1，为最近邻分类。（2）若使用较大的K值，则需要利用x较大邻域的训练样本进行类别预测，使得远离x的训练样本对预测结果也有作用，使预测结果发生错误。最大K=n，每个位置的预测结果为具有最大训练样本数目的类别。

 3.2.2 基于m-fold cross validation的K值选择

以单轮m次交叉验证为例：

STEP1  将训练集随机打乱，均分成m等份，每一份的训练样本数目为N/m

STEP2  对于每个备选K值，如果i在1和m之间，拿出第 i 份作为验证集，其余 m-1 份构成估计集，利用估计集，对验证集的每个样本进行类别预测，得到验证集的预测错误率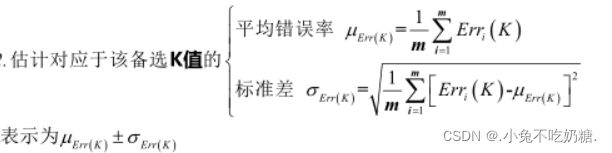

STEP3  取最小的μ对应的K值为最终选择结果。若同时有多个K值有最小μ，则取其中之间最小的μ对应的K值。

3.3 决策规则

3.3.1  多数表决（胜者为王）

 特殊情况的处理：在x的K个近邻N(x)中，多个类别训练样本数目同时最大时，即：存在多个 l∈{1，…，C}，同时满足

 则可以采取如下方式之一，进行x的最终类别预测：①随机选择其中一个类别；②将x分到其最近邻的那个类别；③针对这些类别k个近邻，分别计算相应均值向量，将x分到与其最近的均值向量的那个类别。

3.3.2  基于距离的加权投票

四、K近邻算法的实现 ---- kd树

K近邻法省略了监督式学习阶段，其对任意观测样本x的类别决策从，均依赖于训练集的“记忆”。

两个问题：①如何有效记忆训练集？②如何在记住的训练集内搜索x的K近邻？

训练集的有效记忆 ----- kd树的构建：构建递归二叉树，将d维特征空间的训练集按层划分，形成若干子集，每个子集对应特征空间的一个子区域

x的近邻搜索 ---- 分枝定界法（Branch and Bound,B&B）近邻搜索：对于任意x，将分枝定界法用于kd树，快速搜索测试样本x的近邻

4.1  kd树的构建(CreateKDTree)

kd树是一个以划分方式存储k维空间数量有限的观测点集的数据结构（二叉树）

输入：（1）样本集D = {(xi,yi),i=1,…,N}其所在空间超矩形体Range，其中：

（2）结点分裂的终止条件m0：到达该结点的训练样本数 ≤ m0

输出：kd树结构

STEP1  构造根节点。①确定切分特征split：l = j mod d + 1，选择以x轴切分

②确定切分点：将D内所有样本按照切分特征split取值升序排列，称split取值的中位数为切分点s（not数值，而是下标）；采用垂直于split坐标轴并经过切分点的超平面为切分面

③确定数据集D内经过切分面的样本点，并保存在根结点处；

④切分超矩形区域Range，得到左右子区域：

⑤数据集D的左右子集的生成：

⑥由根节点生成深度为1的左右子节点：

STEP2  左子树的生成：递归调用

STEP3  右子树的生成：递归调用

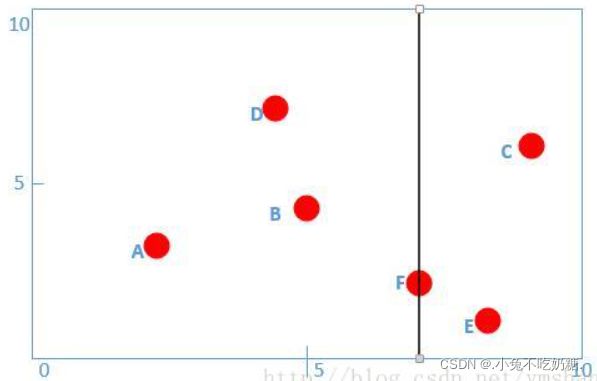
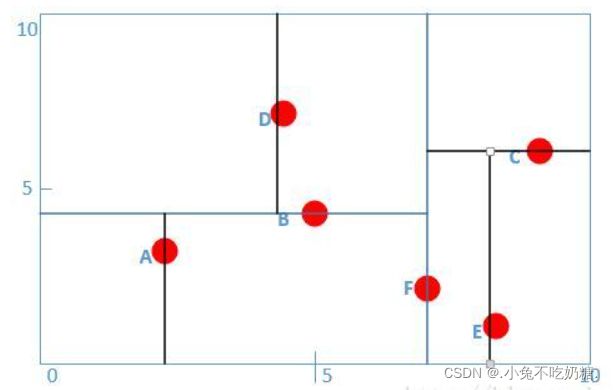
例：给定一个二维空间的数据集：
T = {（2,3），（5,4），（9,6）,（4,7），（8,1），（7,2）}， 构造一个平衡kd树。

为了方便，给各个数据进行编号：A(2，3)、B（5,4）、C（9,6）、D（4,7）、E（8,1）、F（7,2）

可视化数据点如下：

沿x轴进行切分，选出x坐标的中位点，获取根节点的坐标，对数据点按x坐标进行排序得：A(2，3)、D（4,7）、B（5,4）、F（7,2）、E（8,1）、C（9,6）

我们得到中位点为B或F，这里选择F作为根节点，并进行切分，得到左右子树：

对应的树结构为：

此时，B的左孩子为A，右孩子为D，C的左孩子为E，均满足|S|=1，此时r = （r+1）mod 2 = 0，又满足x轴排序，对x轴划分得：

对应树结构为：

4.2 kd树的搜索

算法：基于分枝定界法的kd树搜索

输入：（1）已经构造的kd树

（2）任意观测样本x

输出：x的近邻

STEP1  二叉树搜索，找到含样本x的叶节点

从根节点出发，沿树自上向下，将样本x的切分特征split取值与当前结点切分点s比较

逐级进入生成结点，直到找到kd树中含样本x的叶节点

STEP2  在该叶节点对应的样本子集内搜索，找到初始近邻

将其初始化为样本x的当前最近邻x0，得到二者的距离

STEP3  从该叶节点开始，递归向上回溯

对每个结点重复操作如下：①记当前结点的父节点为q；②以样本x为中心，以当前最近距离d0为半径，构建kd树，则x的真正最近邻x0*一定在该kd树内；③检查kd树是否与当前结点的兄弟结点对应的超矩形体相交，若相交：该兄弟节点所对应的超矩形区域内，可能存在关于x更近的样本，移动至该兄弟节点，递归进行近邻搜索，若存在更近的近邻，则更新近邻及kd树；若不相交：则向上回退，更新当前结点及父节点

STEP4  若回退至根节点，则搜索结束，输出最终的近邻x0*