线性回归练习————线性回归、Anscombe四重奏以及【SVM线性分类】鸢尾花Iris数据集分析

一、线性回练习

1. 一元线性回归练习

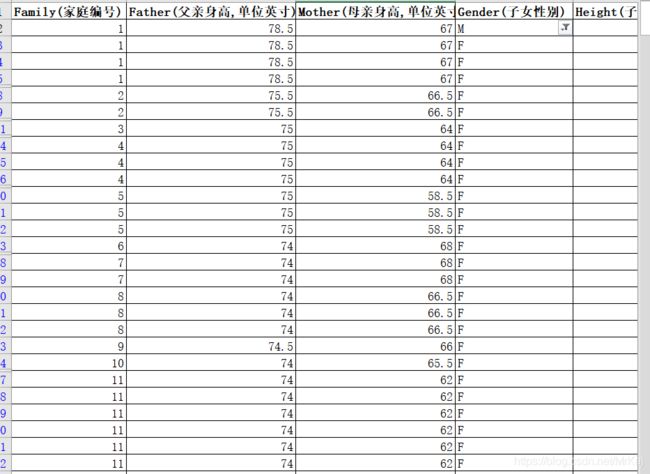
高尔顿数据集进行线性回归分析
父母身高平均值和其中一个子女身高进行回归分析

1. 数据整理，一般获得的数据都会比较多，必须先分析整理数据，以下图为例。
   
   每个家庭中父亲母亲身高肯定一定，所以不用去求平均值，针对每个家庭中子女性别的不同，我分为了两个表
   子表
   

女表

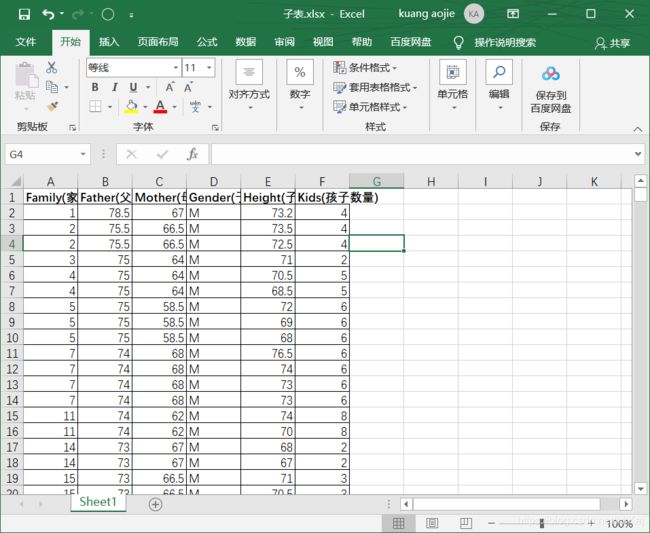
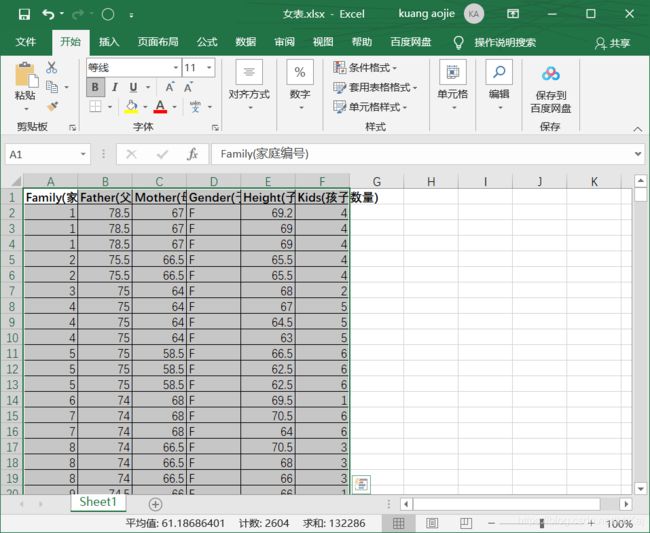
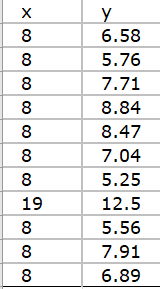
2.因为这两个表中或多或少都会存在家庭编号重复的问题
所以分别对两个表的子女身高求平均值可得新表

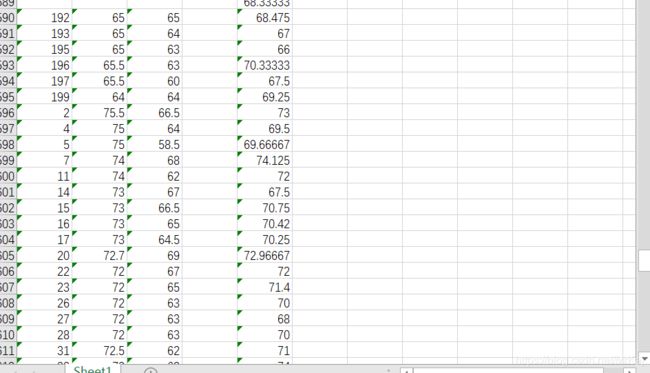
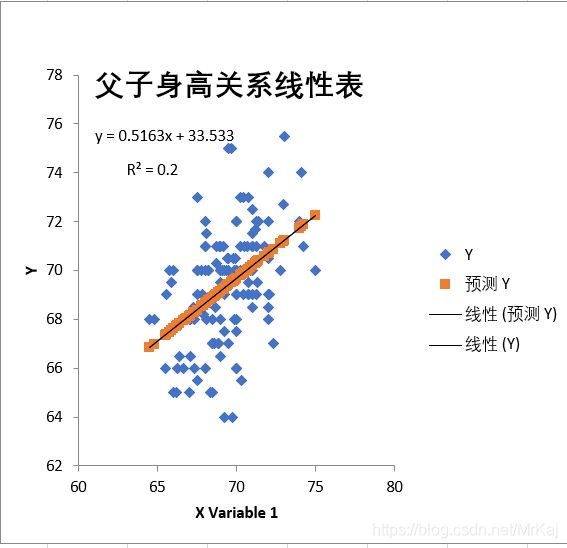
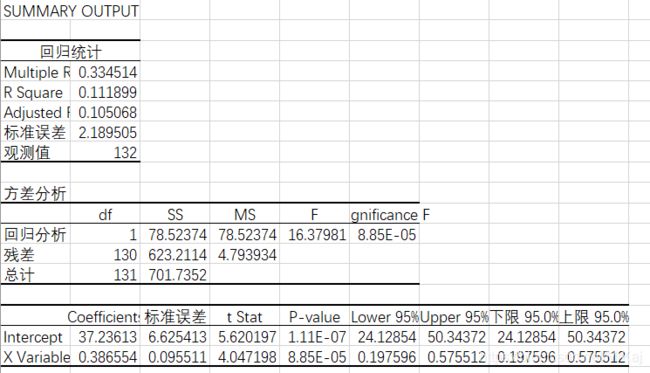
对上述数据分析之后得出结果

父子身高线性表

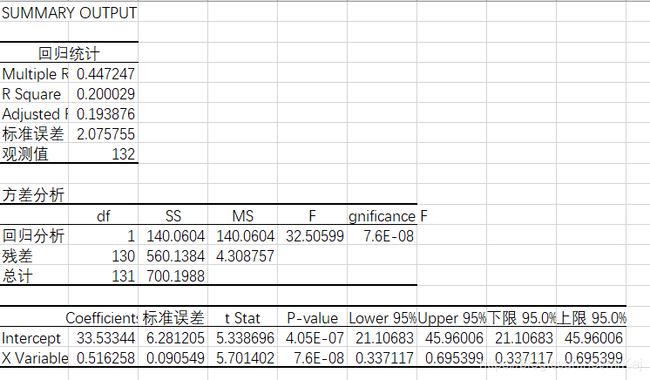
母子身高线性表

二、四重奏数据集分析

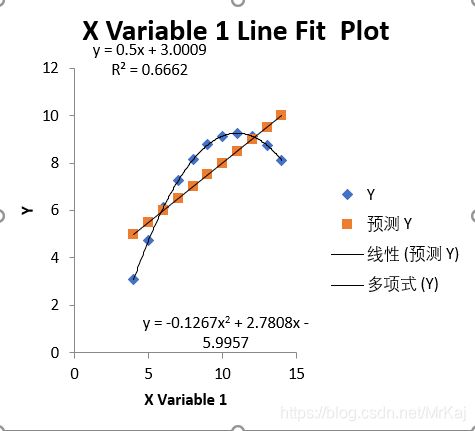
2.1 表一
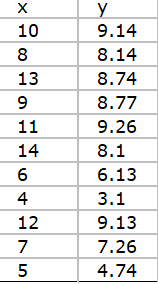
有图看出线性并不是很能够表现原始数据的一个变化趋势，所有该线性回归方程不成立。通过采用其他的回归曲线来测试，发现对于6次的多项式的回归方程来说，会比线性回归方程更好表现数据的变化趋势。

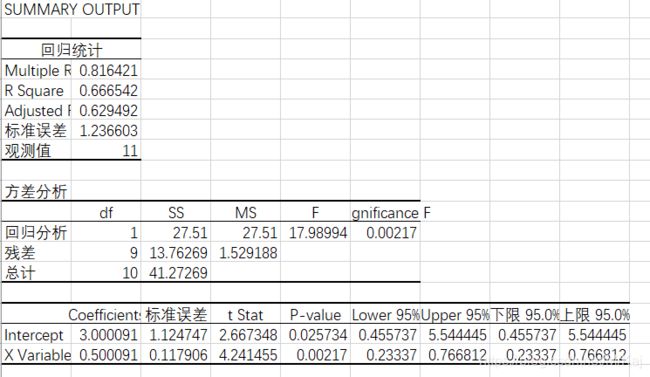
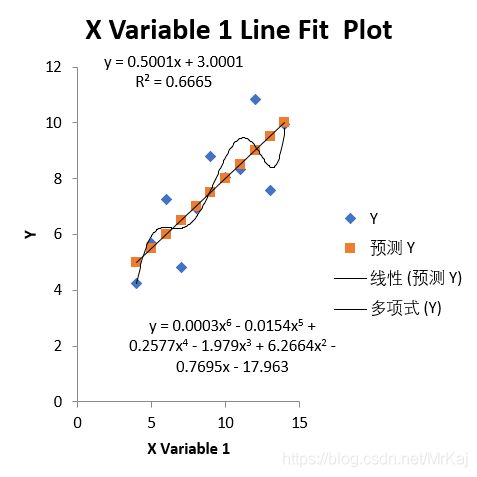
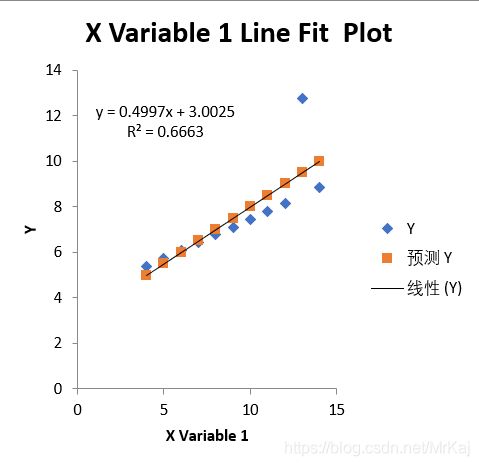
2.2 表二
图中可以看出线性并不是很能够表现原始数据的一个变化趋势，所有该线性回归方程不成立。通过采用其他的回归曲线来测试，发现对于2次的多项式的回归方程来说，会比线性回归方程更好表现数据的变化趋势。

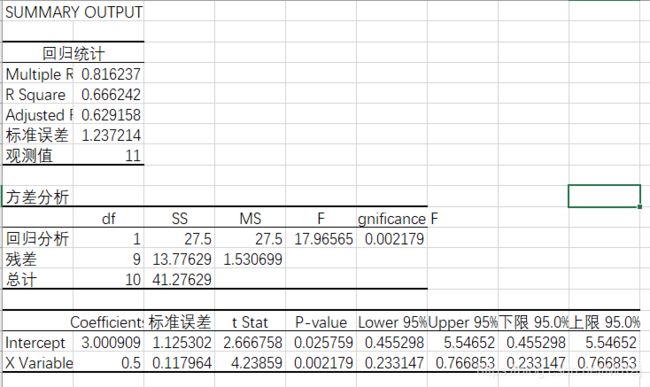
2.3 表三
从图中可以看出线性基本能够表现原始数据的一个变化趋势，只存在极少的极端数据，所有该线性回归方程基本能够体现该数据集的一个变化情况。

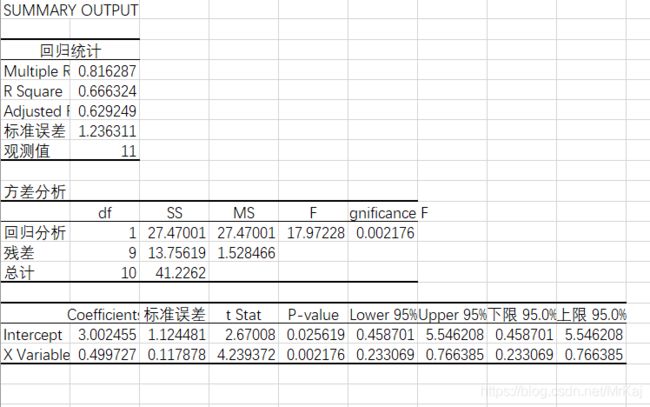
2.4 表四
从图中可以看出线性并不能表现原始数据的一个变化趋势，所有该线性回归方程不成立。可以发现数据基本上不能够用线性来描述，应该将数据自变量和因变量交换位置来进行分析，可能能够用回归数据进行分析。

三【SVM线性分类】鸢尾花Iris数据集实例

3.1.环境搭建

3.1.1 安装Anaconda+python3.7+Jupyter Notebook
3.1.2 创建虚拟环境
运行Anaconda创建虚拟环境XXX,安装自己所需要的工具


3.1.3 也可以使用命令行创建

conda create -n sklearn python=3.7
tf1是自己为创建虚拟环境取的名字，后面python的版本可以根据自己需求进行选择。

至于安装包

pip install 包名 直接这样安装可以由于网络的原因，安装失败或者安装很慢 解决方式：
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple包名此处安装的包包括numpy、pandas、sklearn、matplotlib

2 SVM(支持向量机)

3.2.1 SVM简介

Svm（support Vector Mac）又称为支持向量机，是一种二分类的模型。支持向量机可以分为线性和非线性两大类。其主要思想是找到空间中的一个更够将所有数据样本划开的直线（平面或者超平面），并且使得数据集中所有数据到这个超平面的距离最短。

3.2.2 鸢尾花数据集使用SVM线性分类
LinearSVC（Linear Support Vector Classification）线性支持向量机，核函数是 linear
相关参数说明：

• C:目标函数的惩罚系数C，默认C=10；
• loss：指定损失函数. squared_hinge(默认), squared_hinge；
• penalty ： 惩罚方式，str类型，l1, l2；
• dual ：选择算法来解决对偶或原始优化问题。当nsamples>nfeatures时dual=false；
• tol ：svm结束标准的精度， 默认是 1e - 3；
• multi_class：如果y输出类别包含多类，用来确定多类策略， ovr表示一对多，“crammer_singer”优化所有类别的一个共同的目标 。如果选择“crammer_singer”，损失、惩罚和优化将会被被忽略。；
• max_iter : 要运行的最大迭代次数。int，默认1000。

3.3 源码

导入包

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

获取数据

iris=datasets.load_iris()

X=iris.data

Y=iris.target

数据处理

X=X[:,:2]
Y1=Y[Y<2]
y1=len(Y1)
Y2=Y[Y<1]
y2=len(Y2)
X=X[:y1,:2]

原图

数据归一图
源码：

standardScaler=StandardScaler()
standardScaler.fit(X)
X_standard=standardScaler.transform(X)
svc=LinearSVC(C=1e9)
svc.fit(X_standard,Y1)

画出决策边界：
相关函数说明

• meshgrid() 返回了有两个向量定义的方形空间中的所有点的集合。x0是x值，x1是y的值
• ravel() 将向量拉成一行
• c_[] 将向量排列在一起
• contourf() 等高线

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),# 600个，影响列数
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),# 600个，影响行数
    )
    # x0 和 x1 被拉成一列，然后拼接成360000行2列的矩阵，表示所有点
    X_new = np.c_[x0.ravel(), x1.ravel()]    # 变成 600 * 600行， 2列的矩阵

    y_predict = model.predict(X_new)   # 二维点集才可以用来预测
    zz = y_predict.reshape(x0.shape)   # (600, 600)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
        #print(X_new)
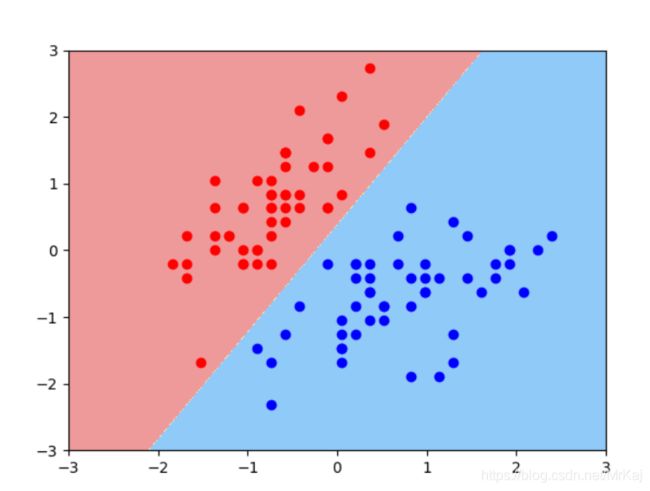
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[0:y2,0], X_standard[0:y2,1],color='red')
plt.scatter(X_standard[y2:y1,0], X_standard[y2:y1,1],color='blue')
plt.show()

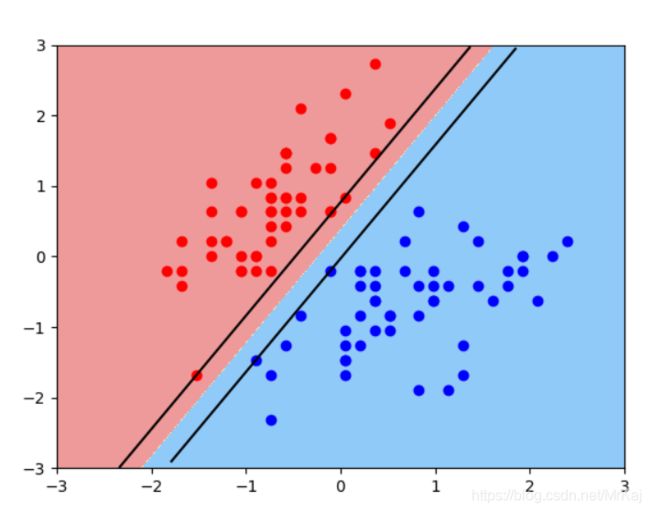
3.4 分类后添加上下边界

def plot_svc_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),# 600个，影响列数
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),# 600个，影响行数
    )
    # x0 和 x1 被拉成一列，然后拼接成360000行2列的矩阵，表示所有点
    X_new = np.c_[x0.ravel(), x1.ravel()]    # 变成 600 * 600行， 2列的矩阵

    y_predict = model.predict(X_new)   # 二维点集才可以用来预测
    zz = y_predict.reshape(x0.shape)   # (600, 600)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
   
    w = model.coef_[0]
    b = model.intercept_[0]
    
    index_x = np.linspace(axis[0], axis[1], 100)
#     f(x,y) = w[0]x1 + w[1]x2 + b
#     1 = w[0]x1 + w[1]x2 + b    上边界
#     -1 = w[0]x1 + w[1]x2 + b   下边界
    y_up = (1-w[0]*index_x - b) / w[1]
    y_down = (-1-w[0]*index_x - b) / w[1]
    
    x_index_up = index_x[(y_up<=axis[3])  & (y_up>=axis[2])]
    x_index_down = index_x[(y_down<=axis[3]) & (y_down>=axis[2])]
    
    y_up = y_up[(y_up<=axis[3])  & (y_up>=axis[2])]
    y_down = y_down[(y_down<=axis[3]) & (y_down>=axis[2])]
    
    plt.plot(x_index_up, y_up, color="black")
    plt.plot(x_index_down, y_down, color="black")

plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[0:y2,0], X_standard[0:y2,1],color='red')
plt.scatter(X_standard[y2:y1,0], X_standard[y2:y1,1],color='blue')
plt.show()

修改C值：C=0.01

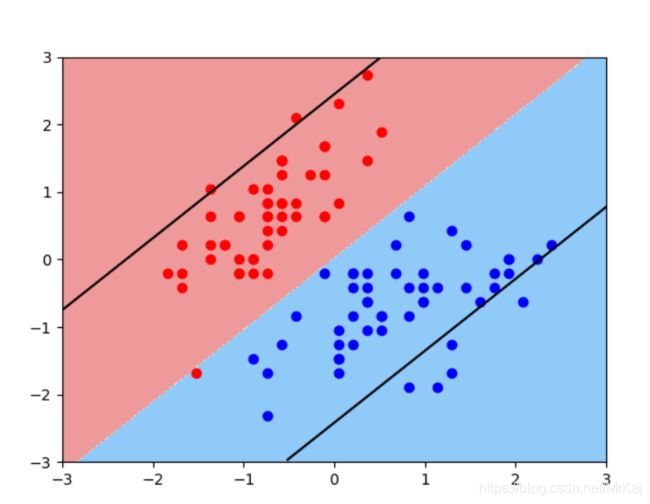
svc = LinearSVC(C=0.01)
svc.fit(X_standard, y)
plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0], X_standard[y==0,1],color='red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1],color='blue')
plt.show()

四、小结

熟悉Excel得使用会使得数据处理变得很简单，我这里得R^2一直等于1有问题，我还在找问题原因。

五、资料引用

SVM线性分类——鸢尾花Iris数据集