深入理解 Batch-Normalization 前向传播 forward /反向传播 backward 以及 代码实现

深入理解 Batch-Normalization

BN 能显著提升神经网络模型的训练速度(论文)，自2015年被推出以来，已经成为神经网络模型的标准层。

现代深度学习框架（如 TF、Pytorch 等）均内置了 BN 层，使得我们在搭建网络轻而易举。但这也间接造成很多人对于 BN 的理解只停留在 概念 层面，而没有深入公式，详细推导其行为 （前向传播+反向传播）。

本文的主旨则是从数学公式层面，详细推导 BN，并通过代码手动实现BN 层。

---

一、BN 的 前向传播

让我们从原论文中最出名的一张图开始吧：

（图1： BN 的前向传播）

BN的前向传播过程分别在不同阶段的行为可以概述如下：

训练阶段：

• 对每个批次的输入 x，[ ‼️重要：在batch 方向上‼️]，计算 均值 ${\mu }_B$ 和 方差 ${\sigma }_B^2$:
  • ${\mu }_B=\frac{1}{m}{\sum }_i^m{x}_i$
  • ${\sigma }_B^2=\frac{1}{m}{\sum }_i^m{(x_i-{\mu }_B)}^2$
• 利用 ${\mu }_B$ 和 ${\sigma }_B^2$ 对输入 x 进行标准化：
  • $\widehat{x_i}=\frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$
• 引入可学习参数 $\gamma$ 和 $\beta$, 对标准化后的 $\widehat{x_i}$ 进行 缩放 和 平移，作为 BN 层的最终输出值：
  • $y_i=\gamma \widehat{x_i}+\beta$

注意：
训练过程 中会以指数平均的方式计算整个训练集的 平均均值(running mean) 和 平均方差(running_var)，这两个值将在 测试阶段 代替 ${\mu }_B$ 和 ${\sigma }_B^2$ 对 x 进行归一化：

• $running\_mean=momentum\ast running\_mean+(1-momentum)\ast {\mu }_B$
• $running\_var=momenutm\ast running\_var+(1-momentum)\ast {\sigma }_B^2$

测试阶段
在这个阶段的计算流程大体与训练阶段相同，但不会计算${\mu }_B$ 和 ${\sigma }_B^2$，而是分别以 running_mean 和 running_var 代替。

说明：

• 对于 Linear 层，设 x 的维度为 [N, D]；那么上面那些公式中的值都是什么维度？
  • ${\mu }_B$ 和 ${\sigma }_B^2$： [D]
  • $\widehat{x_i}$ 和 $y_i$: [N,D]
  • running_mean 和 running_var: [D]
  • $\gamma$ 和 $\beta$: [D]
• 如果是Conv 层，设 x 的维度为 [N, C, H, W]; 那么上面那些公式中的值都是什么维度？
  • 这种情况要特别注意⚠️，对于卷基层，BN 计算均值和方差将会考虑 H 和 W 的维度，在 Pytorch 中称为 BatchNorm2D，如下图所示：
    
    （图2： BatchNorm2D）

---

二、BN 的 反向传播

反向传播的要点是找到 Loss 对当前节点中所有参数的梯度以及对节点的输入张量 x 的梯度，即$\frac{\partial L}{\partial \gamma }$、$\frac{\partial L}{\partial \beta }$ 以及 $\frac{\partial L}{\partial x}$。

由 链式法则可知，这些梯度均等于 上游梯度 * 局部梯度：

• $\frac{\partial L}{\partial \gamma }=\frac{\partial L}{\partial out}\ast \frac{\partial out}{\partial \gamma }$
• $\frac{\partial L}{\partial \beta }=\frac{\partial L}{\partial out}\ast \frac{\partial out}{\partial \beta }$
• $\frac{\partial L}{\partial x}=\frac{\partial L}{\partial out}\ast \frac{\partial out}{\partial x}$

注意：在这些公式中，上游梯度( $\frac{\partial L}{\partial out}$) 是已知的，因此我们只需要求 局部梯度 即可。

方法一：根据计算图求梯度

思路：

为了求得 局部梯度，我们可以把 BN 中每一个计算步骤均绘制成计算图，然后按照计算图反向传播，那么问题就迎刃而解了。

这种方法实现起来特别简单，因为每个步骤的计算公式都是独立的，此时计算局部梯度几乎是轻而易举的事，只需要牢记 链式法则(YYDS)，那么SO EASY！！！

这部分网上有一篇特别棒的文章，非常清晰的讲解了这种方法，搭配了Numpy代码讲解，强烈建议阅读！！ 具体的步骤我就不赘述了，这里只给出我按照种方式实现的 Pytorch 版本。

注： 代码段来源于 密西根大学的计算机视觉课程: EECS 498-007 / 598-005
Deep Learning for Computer Vision 的 Assignment-3 作业.

def backward(dout, cache):

	xhat, gamma, xmu, ivar, sqrtvar = cache
	N = dout.shape[0]
	
	# Step9:
    dbeta = torch.sum(dout, dim=0)
    dgammaxhat = dout
    
    # Step8:
    dgamma = torch.sum(dgammaxhat * xhat, dim=0)
    dxhat = dgammaxhat * gamma
    
    # Step7:
    divar = torch.sum(dxhat * xmu, dim=0)
    dxmu = dxhat * ivar
    
    # Step6:
    dsqrtvar = divar * (-1. / sqrtvar ** 2)
    
    # Step5:
    dvar = dsqrtvar * (0.5 / sqrtvar)
    
    # Step4:
    dsq = dvar * (1. / N)
    
    # Step3:
    dxmu += dsq * 2. * xmu
    
    # Step2:
    dmu = -1. * torch.sum(dxmu, dim=0)
    dx = dxmu
    
    # Step1:
    dx += dmu * (1. / N)

	return dx, dgamma, dbeta

我不会解释这种方法，因为文章中把该解释的都解释了。但我想说的是这种方法不是最优的，因为每一步计算都明确给出了梯度。

事实上，我们可以做的更聪明些，把很多没必要的计算进行“融合”，就像我们计算 sigmoid 的梯度不会精确到每一步计算一样，而是直接写出梯度。下一小节讲重点介绍这种方法。

方法二： BN 的梯度计算 - Analitical Solution

最好的方式是我们首先在纸上计算好梯度，然后直接应用公式得出结果！！

这部分在网上也有几篇博客，推荐大家看下，不过在我尝试了几次后，我发现根据他们的结果我的程序无法得出正确结果！！

• Deriving the Gradient for the Backward Pass of Batch Normalization
• Back Propagation in Batch Normalization Layer

这促使我自己推导公式，下面是完整的步骤。


首先，让我们来回顾一下 BN 中符号，了解中间变量，这可以使我们不会在众多的计算中迷失方向：

• $\mu$ : 等同于上文中的 ${\mu }_B$，表示当前batch的均值（或期望）；
• $v$: 等同于上文中的 ${\sigma }_B^2$，表示当前batch的方差；
• $\sigma$: 等同于上文中的$\sqrt{{\sigma }^2+ϵ}$，表示当前batch的标准差；
• $\gamma$ 和 $\beta$: 缩放 和 平移 参数；
• $y$: 等同于上文中的 $\hat{x}$，表示标准化后的中间张量；
• $z$: BN 的输出张量。
  
  

其次，我们再看看 BN 的简要版计算图，这将帮助我们知道哪些变量会对梯度有贡献：

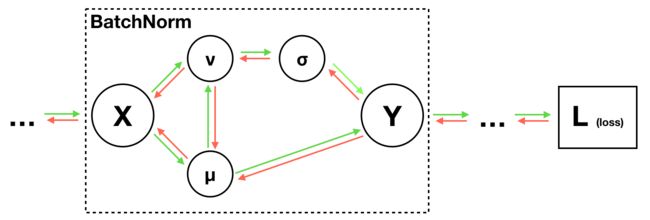
(图3： BN简要计算图）

计算公式如下：

• 1⃣️ $\mu =\frac{1}{N}{\sum }_{j=1}^N{x}_j$
• 2⃣️ $v=\frac{1}{N}{\sum }_{j=1}^N(x_j-\mu {)}^2$ ，
• 3⃣️ $\sigma =\sqrt{v+ϵ}$
• 4⃣️ $y_i=\frac{x_i-\mu }{\sigma }$
• 5⃣️ $z_i=\gamma \ast y_i+\beta$

我们的目的是要计算：

• $\frac{\partial L}{\partial \gamma }$、 $\frac{\partial L}{\partial \beta }$、$\frac{\partial L}{\partial x}$
  
  

1. $\frac{\partial L}{\partial \gamma }$ 的计算

由 链式法则 可知: $\frac{\partial L}{\partial \gamma }=\frac{\partial L}{\partial z}\ast \frac{\partial z}{\partial \gamma }$

注意：

• 上式中 z 是矩阵，直接计算矩阵的梯度比较难，那么我们不妨先对某一个单独的输入$x_i$计算梯度，然后应用到整个矩阵。
• 不要忘了，$\frac{\partial L}{\partial z}$ 是 上游梯度，在当前节点这是已知值，我们只需要计算 局部梯度。

对于某一个单独的输入$z_i$，我们计算梯度： $\frac{\partial z_i}{\partial \gamma }=y_i$

显然所有 $\frac{\partial z_i}{\partial \gamma }$ 都会对 $\frac{\partial L}{\partial \gamma }$ 有贡献，因此不难得出结论1⃣️：

• 1⃣️ $\frac{\partial L}{\partial \gamma }={\sum }_{j=1}^N\frac{\partial L}{\partial z_j}\ast y_j$

2. $\frac{\partial L}{\partial \beta }$ 的计算

同 $\frac{\partial L}{\partial \gamma }$ 计算原理相同，我们很容易就能得出结论2⃣️：

• 2⃣️ $\frac{\partial L}{\partial \beta }={\sum }_{j=1}^N\frac{\partial L}{\partial z_j}\ast 1={\sum }_{j=1}^N\frac{\partial L}{\partial z_j}$

3. $\frac{\partial L}{\partial x}$ 的计算

这部分最难，中间变量众多，我们得非常小心。查看计算图可知，x 对三个变量有直接贡献：$\mu$、$v$ 和 $Y$ 。

其中 X -> $Y$ 这条连接在图3中没有画出来，但我们从公式4⃣️知道，这确实存在！由此可知：

• $\frac{\partial L}{\partial x_i}=\frac{\partial L}{\partial y_i}\ast \frac{\partial y_i}{\partial x_i}+\frac{\partial L}{\partial v}\ast \frac{\partial v}{\partial x_i}+\frac{\partial L}{\partial u}\ast \frac{\partial u}{\partial x_i}$

我们一项一项来。

第一项：$\frac{\partial L}{\partial y_i}\ast \frac{\partial y_i}{\partial x_i}$:

• $\frac{\partial L}{\partial y_i}$:
  由于 $y_i$ 只对 $z_i$ 有贡献，因此：$\frac{\partial L}{\partial y_i}=\frac{\partial L}{\partial z_i}\ast \frac{\partial z_i}{\partial y_i}=\frac{\partial L}{\partial z_i}\ast \gamma$
• $\frac{\partial y_i}{\partial x_i}$:
  这一项是指 $x_i$ 对$y_i$ 的直接贡献，由公式4⃣️可知：$\frac{\partial y_i}{\partial x_i}=\frac{1}{\sigma }$

综上可得： $\frac{\partial L}{\partial y_i}\ast \frac{\partial y_i}{\partial x_i}=\frac{\partial L}{\partial y_i}\ast \frac{1}{\sigma }$

第二项：$\frac{\partial L}{\partial v}\ast \frac{\partial v}{\partial x_i}$

• $\frac{\partial v}{\partial x_i}$:
  • 由公式2⃣️，$\frac{\partial v}{\partial x_i}=\frac{1}{N}\ast 2\ast (x_i-\mu )$
• $\frac{\partial L}{\partial v}={\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{\partial y_j}{\partial v}={\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{\partial y_j}{\partial \sigma }\frac{\partial \sigma }{\partial v}$
  • 由公式3⃣️，$\frac{\partial \sigma }{\partial v}=\frac{1}{2\sigma }$
  • 由公式4⃣️，$\frac{\partial y_j}{\partial \sigma }=-\frac{x_j-\mu }{{\sigma }^2}$

综上可得：

• $\frac{\partial L}{\partial v}\ast \frac{\partial v}{\partial x_i}={\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{-(x_j-\mu )}{{\sigma }^2}\frac{1}{2\sigma }\ast \frac{2(x_i-\mu )}{N}$
• 注意到 $\frac{x_j-\mu }{\sigma }=y_j$，则上式化简为：
  • $\frac{\partial L}{\partial v}\frac{\partial v}{\partial x_i}=\frac{x_i-\mu }{\sigma }\frac{-1}{\sigma N}{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{x_j-\mu }{\sigma }=\frac{y_i}{\sigma }\frac{-1}{N}{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}{y}_j$

第三项：$\frac{\partial L}{\partial u}\ast \frac{\partial u}{\partial x_i}$

• $\frac{\partial u}{\partial x_i}=\frac{1}{N}$
• $\frac{\partial L}{\partial u}$:
  • 因为$v$ 是 $\mu$的函数，因此:
    $\frac{\partial L}{\partial u}={\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{\partial y_i}{\partial u}+{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{\partial y_j}{\partial v}\frac{\partial v}{\partial u}$
  • 由于 $\frac{\partial v}{\partial u}=\frac{1}{N}{\sum }_{j=1}^N(x_j-\mu )(-2)=0$, 因此上式第二项为 0。
  • 由公式4⃣️， $\frac{\partial y_j}{\partial u}=\frac{-1}{\sigma }$
  • 因此， $\frac{\partial L}{\partial u}={\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{\partial y_j}{\partial u}={\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{-1}{\sigma }$

综上可得：$\frac{\partial L}{\partial u}\ast \frac{\partial u}{\partial x_i}={\sum }_{j=1}^N\frac{\partial L}{\partial y_j}\frac{\partial y_i}{\partial u}\frac{\partial u}{\partial x_i}=\frac{-1}{N\sigma }{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}$

综合所有上述三项结果，最终:

$\frac{\partial L}{\partial x_i}=\frac{1}{\sigma }\frac{\partial L}{\partial y_i}-\frac{y_i}{N\sigma }{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}{y}_j-\frac{1}{\sigma }\frac{1}{N}{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}$

稍作整理：

$\frac{\partial L}{\partial x_i}=\frac{1}{\sigma }(\frac{\partial L}{\partial y_i}-\frac{1}{N}{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}-\frac{y_i}{N}{\sum }_{j=1}^N\frac{\partial L}{\partial y_j}{y}_j)$

向量化结果：

$\frac{\partial L}{\partial X}=\frac{1}{\sigma }(\frac{\partial L}{\partial Y}-E[\frac{\partial L}{\partial Y}]-Y\ast E[\frac{\partial L}{\partial Y}\ast Y])$

使用 Pytorch 编写代码如下：

def backward(dout, cache):

	xhat, gamma, ivar = cache
        
    dbeta = torch.sum(dout, dim=0)
    dgamma = torch.sum(dout * xhat, dim=0)
    
    dy = dout * gamma
    dx = ivar * (dy - torch.mean(dy, dim=0) - xhat * torch.mean(dy * xhat, dim=0))

---

结语

最后让我们测试下两种计算方法的结果，并看看计算速度的对比:

from convolutional_networks import BatchNorm

reset_seed(0)
N, D = 128, 2048
x = 5 * torch.randn(N, D, dtype=torch.float64, device='cuda') + 12
gamma = torch.randn(D, dtype=torch.float64, device='cuda')
beta = torch.randn(D, dtype=torch.float64, device='cuda')
dout = torch.randn(N, D, dtype=torch.float64, device='cuda')

bn_param = {'mode': 'train'}
out, cache = BatchNorm.forward(x, gamma, beta, bn_param)

t1 = time.time()
dx1, dgamma1, dbeta1 = BatchNorm.backward(dout, cache)
t2 = time.time()
dx2, dgamma2, dbeta2 = BatchNorm.backward_alt(dout, cache)
t3 = time.time()

print('dx difference: ', eecs598.grad.rel_error(dx1, dx2))
print('dgamma difference: ', eecs598.grad.rel_error(dgamma1, dgamma2))
print('dbeta difference: ', eecs598.grad.rel_error(dbeta1, dbeta2))
print('speedup: %.2fx' % ((t2 - t1) / (t3 - t2)))

代码运行结果如下：

dx difference:  1.1126357877489443e-16
dgamma difference:  0.0
dbeta difference:  0.0
speedup: 1.58x

由此可见，我们通过公式计算得到的梯度与通过计算图反向传播得到的梯度没有差别，但前者的计算速度是后者的 1.58 倍。