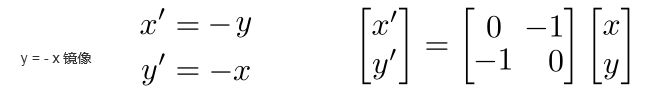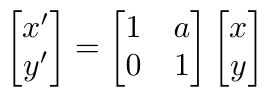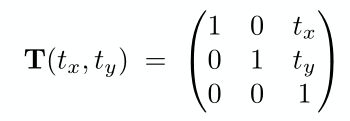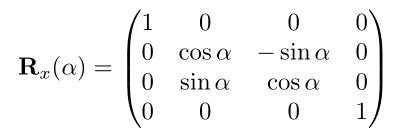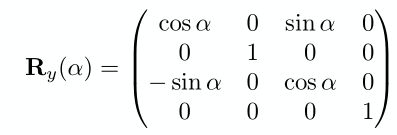计算机图形学(三)-图形学中的基本变换(缩放、平移、旋转、剪切、镜像)
图形学中的基本变换
- 1. 二维变换
-
- 1.1 缩放变换
- 1.2.镜像变换
- 1.3 剪切变换
- 1.4 旋转变换
- 1.5 平移变换
-
- 1.5.1 什么是线性变换
- 1.5.2 平移变换(仿射变换)
- 1.5.3 平移变换齐次坐标表示(线性)
- 1.6 逆变换
- 1.7 组合变换
- 1.8 非原点的旋转变换
- 1.9 刚体变换
- 1.10 二维主要变换总结
- 2 三维变换
-
- 2.1 三维平移变换
- 2.2 三维缩放矩阵
- 2.3 三维旋转矩阵
-
- 2.3.1 绕z轴旋转矩阵
- 2.3.2 绕x轴旋转矩阵
- 2.3.3 绕y轴旋转矩阵
- 2.3.4 绕任意轴旋转矩阵
1. 二维变换
1.1 缩放变换
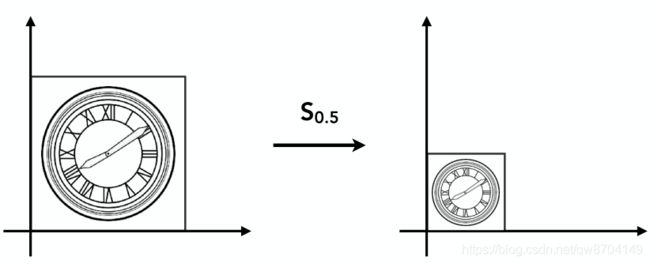
如上图,如果想把一个图形缩小为原来的0.5倍,那么就需要x坐标变为0.5倍,y坐标也变为0.5倍,可以用以下表达式表示
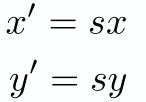
前面两节已经学了一些矩阵方面的知识,那么这两个表达式可以用矩阵的形式表示如下
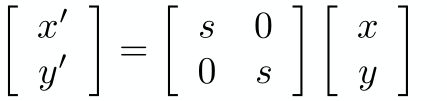
上面的矩阵表达式针对x轴和y轴进行相同比例的缩放,实际中两个方向上的缩放可能不尽相同,例如x轴缩放为0.5倍与轴不缩放,这时只需要把矩阵表达式稍作修改即可
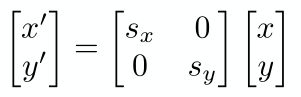
Sx表示在x轴方向上缩放的倍数,Sy表示在y轴方向上缩放的倍数
1.2.镜像变换
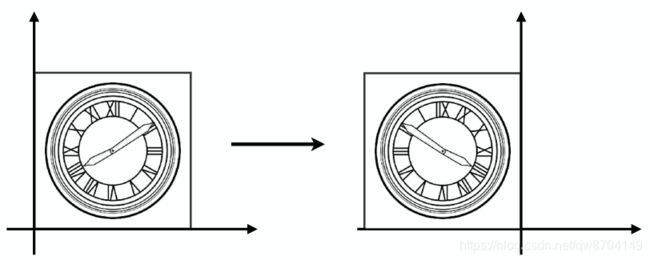
如上图需要将物体以y轴进行镜像,那么可以用以下表达式表达
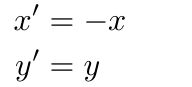
也可以用矩阵形式的表达

一些其他镜像矩阵
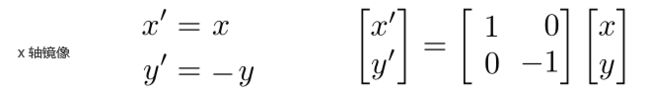
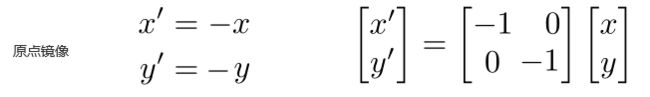
1.3 剪切变换
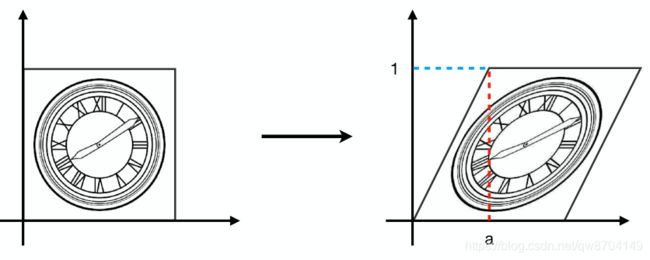
如上图这个变换好像是拽着图形的右上角沿着x轴向右拉了一段距离,称为剪切变换。
剪切变换有以下特点
- 变换后物体的y坐标保持不变
- x坐标在最高的点平移了a,最低点没有移动
- 其它的点移动距离a * Y (Y表示物体上点的y坐标值)
1.4 旋转变换
说旋转,默认指的是 绕原点(0,0)逆时针旋转,下图是物体绕原点逆时针旋转θ角的示意图
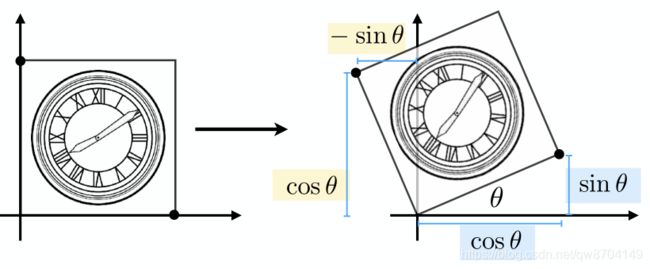
以上变换同样可以写成矩阵的形式
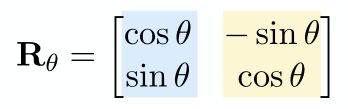
1.5 平移变换
1.5.1 什么是线性变换
什么是线性变换,前面提到的变换都可以使用以下表达式表示
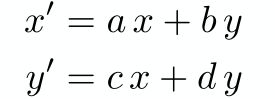
都可以使用矩阵形式表示为

继而表示为:输出坐标 = 变换矩阵 × 输入坐标 的形式
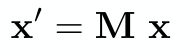
满足以上条件的变换称为 线性变换
1.5.2 平移变换(仿射变换)

如上图需要把一个图形沿x轴平移tx,沿y轴平移ty,可以用以下表达式表示

你会发现,它 无法用前面熟悉的线性变换矩阵的形式表示,也就是说平移变换是非线性变换
只能用以下矩阵形式表示,上面把这种变换称为非线性变换,其实它有专门的名字叫仿射变换
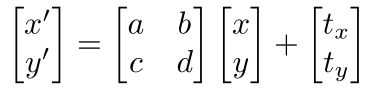
人们总是希望能有一个统一的方法来表示同类事物,希望平移变换也能够像其他变换一样用同样的形式表示,使用起来更加便捷统一。
前辈大牛们经过各种尝试,想出了一个办法,就是引入齐次坐标
1.5.3 平移变换齐次坐标表示(线性)
什么是齐次坐标
齐次坐标与笛卡尔坐标系相比,会比笛卡尔坐标系多出一维,例如原来的坐标系是二维,转为齐次坐标系后就会变成三维,如果在卡尔坐标系上有点(x,y);当转换为齐次坐标后这个点变为(wx,wy,w);反过来同样适用,如果在其次坐标系中有一个点(x,y,w),转换到笛卡尔坐标系下,这个点应该表示为(x/w,y/w),一个点在齐次坐标下有无数的表示法,例如笛卡尔坐标系下有点(1,2),在其次坐标系下它可以表示为(1,2,1)、(2,4,2)、(3,6,3) …
点和向量转为齐次坐标表示
向量(x,y)转为齐次坐标表示为
![]()
这里解释一下在转为齐次坐标的过程中,点在末尾添加1,而向量添加0。
向量具有平移不变形,任何一个向量平移后表示原来的向量,在向量转为齐次坐标形式的时候,在末尾添加0,就是为了保护这个向量在平移过程中不发生变化。
平移变换齐次坐标表示
平移变换原本是仿射变换,通过引入齐次坐标后,可以使用线性变换的形式表示

这样我们的目的就达到了,把平移变换也表示为一个矩阵乘以一个坐标的线性变换的形式
1.6 逆变换
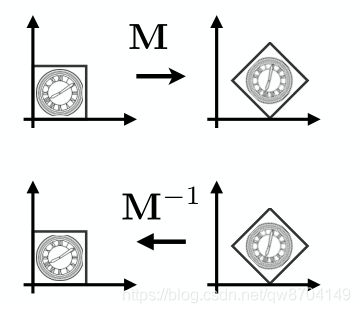
一个物体做一个变换,变换完以后要恢复到原来的位置,变换回原来的位置的过程称为逆变换,逆变换在数学上的实现是乘以变换矩阵的 逆矩阵
1.7 组合变换
组合变换就是对一个物体进行多个变换,例如同时进行平移和旋转变换
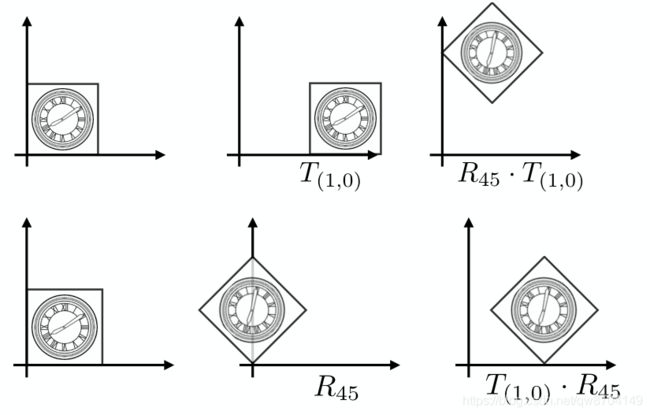
上图中有两套组合变换
- 先平移(1,0),再旋转45度
- 先旋转45度,再平移(1,0)
你会发现虽然都作了相同的变换,但是变换的顺序不同最终的结果也不同,是因为矩阵A乘矩阵B与矩阵B乘矩阵A的结果不同(上一节学习的矩阵相乘性质)
组合变换矩阵相乘应用的顺序

上图中A1,A2一直到An表示变换矩阵,一个点进行组合变换时,应用在该点的矩阵是从右到左。即矩阵An乘An-1一直乘到A1,实际应用到点的顺序是A1,A2一直到An
矩阵乘法结合律使用
之前的学习中我们知道矩阵相乘交换律不适用,但是适用结合律,既然适用有什么妙用,接下来看看
一个点做多个变换即多个矩阵相乘再乘以这个点,根据矩阵乘法结合律,可以先把这些矩阵相乘,乘完在与这个点相乘,只要保证矩阵相乘的顺序不变即可
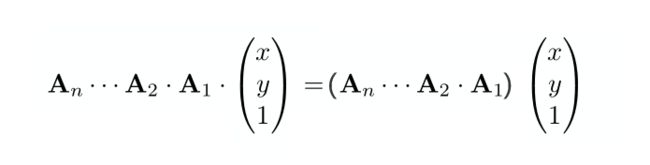
1.8 非原点的旋转变换
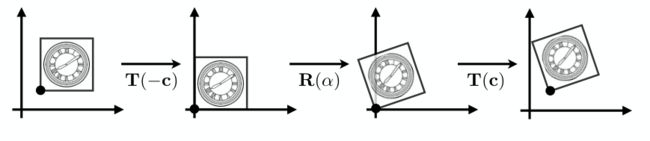
我们学会了物体绕原点旋转,对于一个不是绕原点旋转的变换需要换个思维实现,实现过程分三步
- 将物体旋转要绕的点移动到原点,
- 移到原点后做旋转变换
- 旋转变换完成后平移回原来的位置
这个过程用一个表达式表示
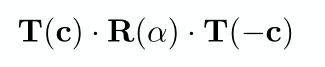
矩阵变换作用在物体上的顺序是从右到左,所以上面表达式表示,先平移T(-c)到原点,然后旋转R(α),最后平移到原来位置T(c),一定要注意先后顺序
1.9 刚体变换
只有平移和旋转组成的变换称为刚体变换,例如一个物体先旋转45度在x轴方向上平移一个单位,这样的变换称为刚体变换,刚体变换的本质是一个物体的位置和角度发生了变换,物体本身的形状并不发生任何变化
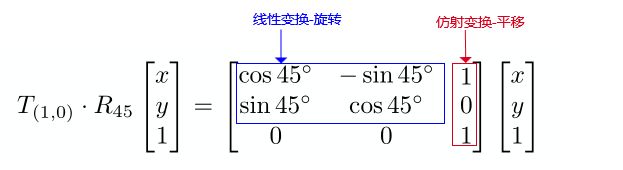
假如有一个刚体变换先逆时针旋转45度,在沿x轴平移1个单位,那么这个变换可以用下面的矩阵表示

上面的变换是先进行线性变换-旋转,在进行仿射变换-平移,这时可以把两个变换的矩阵合并为一个矩阵,之所以可以合并因为在同一个矩阵同时表示两种变换时,会先进行线性变换再进行仿射变换,这与我们提到的变换顺序是一致的,两种变换合并为一个矩阵用来表示刚体变换,这个矩阵称为刚体变换矩阵
刚体变换的逆变换
二维刚体变换的逆变换矩阵,只需要把原变换矩阵左上角2×2矩阵(上图蓝色框部分)转置,右侧最后一列(上图红色框部分)的平移分量符号取反。就可以得到刚体变换的逆变换矩阵
1.10 二维主要变换总结
图形变换中的三大变换为缩放、旋转、平移。下面把这三类变换的变换矩阵罗列一下,方便日后使用
缩放矩阵

![]()
旋转矩阵
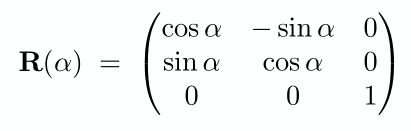
上述旋转矩阵是绕原点逆时针旋转的变换矩阵,当需要得到顺时针旋转的变换矩阵时,可以通过顺时针旋转的变换矩阵进行逆变换得到逆时针旋转的变换矩阵,即
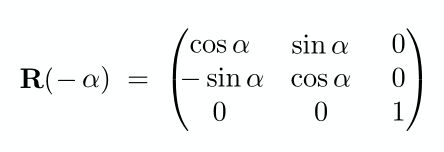
你会发现这个矩阵不就是逆时针旋转变换矩阵的转置矩阵,没错就是这样的,旋转变换矩阵的逆矩阵与转置矩阵就是同一个矩阵。像这样一个矩阵的转置等于这个矩阵的逆,我们称这个矩阵是 正交矩阵
2 三维变换
2.1 三维平移变换
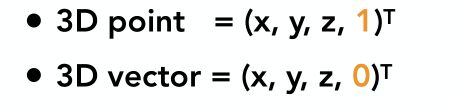
三维坐标系转为齐次坐标,与二维坐标系转为齐次坐标类似,一个点在末尾添加1,一个向量添加0。
二维平移矩阵是仿射变换,可以转换到齐次坐标下使用线性变换的形式表示,三维平移矩阵也是仿射变换,同样的道理也可以转换到齐次坐标下用线性变换矩阵的形式表示,下图就是齐次坐标下三维平移变换矩阵
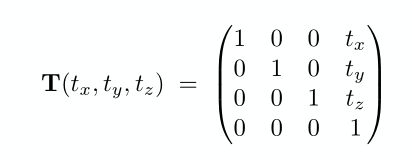
2.2 三维缩放矩阵
我们知道了而是缩放矩阵了,那么推理三维缩放矩阵非常简单,就是在矩阵中增加一维z分量即可,三维缩放矩阵就可以表示如下
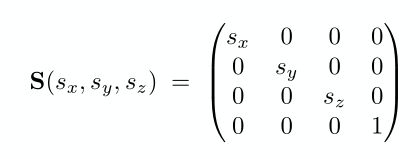
2.3 三维旋转矩阵
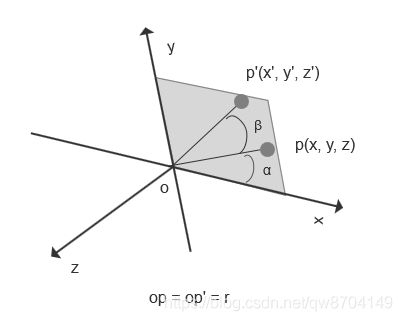
2.3.1 绕z轴旋转矩阵
如上图,若有一点p在x轴和y轴所在平面上,p到到原点o的距离为r,即op=op’=r;p点到原点o的连线与x轴的夹角是α,p点绕z轴旋转β角,p点旋转到p’点的位置,则可以得到以下关系
x = cos(α)*r
y = sin(α)*r
x' = cos(α+β)*r
y' = sin(α+β)*r
三角函数两角求和公式
cos(α+β) = cos(α)*cos(β) - sin(α)*sin(β)
sin(α+β) = sin(α)*cos(β) + cos(α)*sin(β)
使用上面的关系和三角函数求和公式得到
x' = cos(α+β)*r
= (cos(α)*cos(β) - sin(α)*sin(β))*r
= (cos(α)*r)*cos(β) - (sin(α)*r)*sin(β) //将x1 = cos(α)*r 和 y1 = sin(α)*r 带入
= x*cos(β) - y*sin(β)
y' = sin(α+β)*r
= (sin(α)*cos(β) + cos(α)*sin(β))*r
= (sin(α)*r)*cos(β) + (cos(α)*r)*sin(β) //将x1 = cos(α)*r 和 y1 = sin(α)*r 带入
= y*cos(β) + x*sin(β)
= x*sin(β) + y*cos(β)
z' = z
上面得到的结果是绕z轴旋转β角的结果,把β替换为α则有
2.3.2 绕x轴旋转矩阵
2.3.3 绕y轴旋转矩阵
2.3.4 绕任意轴旋转矩阵
绕任意轴旋转可分解为绕x轴旋转α角,绕y轴旋转β角,绕z轴旋转γ角,用以下形式表示
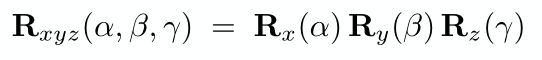
将绕绕三轴旋转转化为绕一个单位向量n旋转α角,向量n默认穿过原点,用下面的矩阵表示
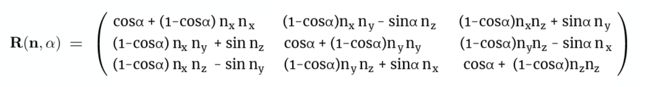
上面这个公式只适用于绕穿过原点的向量旋转变换,如果遇到绕任意轴时怎么办?
在二维空间中旋转若不是绕原点旋转,需要先平移到原点,再作旋转,最后要平移回原来的位置,三维空间中绕未穿原点的向量旋转,可以先将旋转轴平移至穿过原点,进行旋转,旋转完成后再进行平移的逆变换,将物体移回原来位置