神经网络与深度学习-chapter2 反向传播算法
英语原文:Neural Networks and Deep Learning(Michael Nielsen)
中文译文:神经网络与深度学习(Michael Nielsen)
第2章 反向传播算法如何工作
1、一种基于矩阵的快速计算神经网络输出的方法
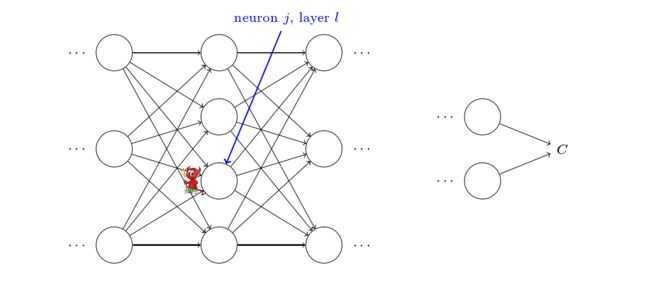
从符号开始,用 w j k l w_{j k}^{l} wjkl来表示第 ( l − 1 ) (l-1) (l−1)层的第 k k k个神经元连接到第 l l l层的第 j j j个神经元的权重
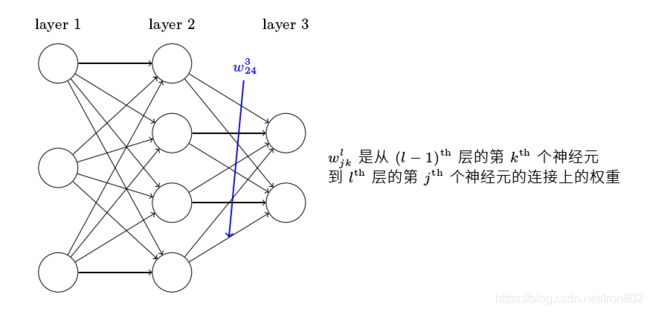
用相似的方法,我们可以表示偏值 b b b 和激活值 a a a
- 用 b j l b_{j}^{l} bjl来表示(第 l l l层的第 j j j个神经元)的偏值;
- 用 a j l a_{j}^{l} ajl来表示(第 l l l层的第 j j j个神经元)的激活值;
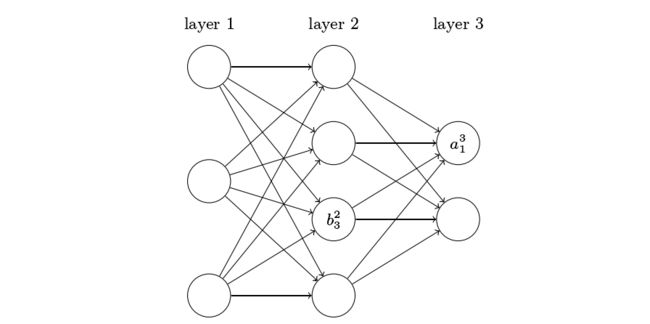
由此,第 l l l层第 j j j个神经元的激活 a j l a_{j}^{l} ajl可由第 ( l − 1 ) (l-1) (l−1)层的各激活值 a k l − 1 a_{k}^{l-1} akl−1加权 w j k l w_{jk}^{l} wjkl并加上该神经元的阈值 b j l b_{j}^{l} bjl后代入激活函数 σ ( ⋅ ) \sigma(·) σ(⋅)求得,其中求和是在( l − 1 l-1 l−1)层的所有k个神经元上进行的。 a j l = σ ( ∑ k w j k l a k l − 1 + b j l ) \color{red}{a_{j}^{l}=\sigma\left(\sum_{k} w_{j k}^{l} a_{k}^{l-1}+b_{j}^{l}\right)} ajl=σ(k∑wjklakl−1+bjl) 为用矩阵形式表达上式,定义一个权值矩阵 w l w^l wl用于表示第 ( l − 1 ) (l-1) (l−1)层到第 l l l层的权重,在这个矩阵中的第 j j j行第 k k k列的元素即为 w j k l w_{jk}^l wjkl。用同样的方法,我们可以定义偏值向量 b l b^l bl和激活值向量 a l a^l al。
最后我们需要引入向量化函数 σ \sigma σ,函数具有以下特性: σ ( v ) j = σ ( v j ) \sigma(v)_{j}=\sigma\left(v_{j}\right) σ(v)j=σ(vj)如当激活函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2时,应具有下列特性:
f ( [ 2 3 ] ) = [ f ( 2 ) f ( 3 ) ] = [ 4 9 ] f\left(\left[\begin{array}{l}2 \\ 3\end{array}\right]\right)=\left[\begin{array}{l}f(2) \\ f(3)\end{array}\right]=\left[\begin{array}{l}4 \\ 9\end{array}\right] f([23])=[f(2)f(3)]=[49]最后对照(第 l l l层的第 j j j个神经元)的激活值 a j l a_j^l ajl的表达式,我们可以得到第 l l l层激活函数 a l a^l al的矩阵求解方式:
a l = σ ( w l a l − 1 + b l ) \color{red}{a^{l}=\sigma\left(w^{l} a^{l-1}+b^{l}\right)} al=σ(wlal−1+bl)为进一步简化,我们定义了加权输入向量 z l z^l zl:
z l ≡ w l a l − 1 + b l \color{red}{z^{l} \equiv w^{l} a^{l-1}+b^{l}} zl≡wlal−1+bl则 a l = σ ( z l ) \color{red}{a^{l}=\sigma\left(z^{l}\right)} al=σ(zl)它是由第 l l l层各神经元的加权输入组成的,其中第 l l l层的第 j j j个神经元的加权输入 z j l z_j^l zjl可以表示为: z j l = ∑ k w j k l a k l − 1 + b j l \color{red}{z_{j}^{l}=\sum_{k} w_{j k}^{l} a_{k}^{l-1}+b_{j}^{l}} zjl=k∑wjklakl−1+bjl
2、关于代价函数的两个假设
二次代价函数:
C = 1 2 n ∑ x ∥ y ( x ) − a L ( x ) ∥ 2 \color{red}{C=\frac{1}{2 n} \sum_{x}\left\|y(x)-a^{L}(x)\right\|^{2}} C=2n1x∑∥∥y(x)−aL(x)∥∥2其中 n 是训练样本的总数;求和运算遍历了每个训练样本 x;y = y(x) 是对应的目标输出;aL(x) 是当网络输入为x时最后一层的激活值。
① 假设1:代价函数可以用每一个样本的代价函数 C x C_x Cx的平均值表示,即
C = 1 n ∑ x C x C x = 1 2 ∥ y − a L ∥ 2 \begin{gathered}C=\frac{1}{n} \sum_{x} C_{x} \\C_{x}=\frac{1}{2}\left\|y -a^{L}\right\|^{2}\end{gathered} C=n1x∑CxCx=21∥∥y−aL∥∥2因为,当用反向传播算法计算的时候是针对单个样本的,即计算每个样本的 ∂ C x ∂ w \frac{\partial C_{x}}{\partial w} ∂w∂Cx和 ∂ C x ∂ b \frac{\partial C_{x}}{\partial b} ∂b∂Cx,最后再取均值求整个样本集的 ∂ C ∂ w \frac{\partial C}{\partial w} ∂w∂C和 ∂ C ∂ b \frac{\partial C}{\partial b} ∂b∂C。
② 假设2:损失函数只与神经网络的输出值 a l a^l al有关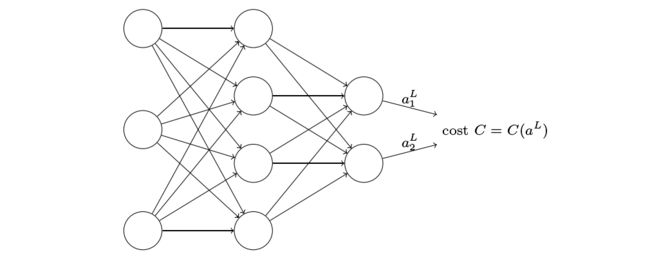
二次代价函数MSE满足该条件,因为对于⼀个单独的训练样本 x 其⼆次代价函数可以写作: C = 1 2 ∥ y − a L ∥ 2 = 1 2 ∑ j ( y j − a j L ) 2 \color{red}{C=\frac{1}{2}\left\|y-a^{L}\right\|^{2}=\frac{1}{2} \sum_{j}\left(y_{j}-a_{j}^{L}\right)^{2}} C=21∥∥y−aL∥∥2=21j∑(yj−ajL)2其中样本 x x x矩阵的行 i i i代表样本的数量,矩阵的列 j j j代表一个样本中的特征数,该式即是将一个样本按特征数 j j j展开得到的式子,可以看到这是一个关于输出激活值的函数,对最后一层所有激活值带入运算得到了 C C C。
注:二次代价函数并不依赖于y,因为当输⼊的训练样本 x 是固定的,y就是一个固定的。
3、Hadamard乘积, s ⊙ t \mathbf{s} \odot \mathbf{t} s⊙t
s ⊙ t \mathbf{s} \odot \mathbf{t} s⊙t表示矩阵按元素的乘积,其中 s 、 t s、t s、t是两个相同维度的向量,有 ( s ⊙ t ) j = s j t j (\mathbf{s} \odot \mathbf{t})_j = s_jt_j (s⊙t)j=sjtj,被称为哈达玛积,如:
[ 1 2 ] ⊙ [ 3 4 ] = [ 1 ∗ 3 2 ∗ 4 ] = [ 3 8 ] \left[\begin{array}{l}1 \\ 2\end{array}\right] \odot\left[\begin{array}{l}3 \\ 4\end{array}\right]=\left[\begin{array}{l}1 * 3 \\ 2 * 4\end{array}\right]=\left[\begin{array}{l}3 \\ 8\end{array}\right] [12]⊙[34]=[1∗32∗4]=[38]
4、反向传播的四个基本方程
反向传播阐述了怎样改变权值和偏值从而改变网络输出值。
首先我们介绍一个中间量 δ j l \delta_{j}^{l} δjl,我们称它为第 l l l层的第 j j j个神经元的误差,反向传播算法讲述了如何计算 δ j l \delta_{j}^{l} δjl,以及通过 δ j l \delta_{j}^{l} δjl如何计算 ∂ C ∂ w j k l \frac{\partial C}{\partial w_{j k}^{l}} ∂wjkl∂C及 ∂ C ∂ b j l \frac{\partial C}{\partial b_{j}^{l}} ∂bjl∂C。
- 这个恶魔在第 l l l层的第 j j j个神经元上,当有输入将要进入这个神经元时,恶魔可以通过在将流入该神经元的加权输入 z j l z_j^l zjl中增加任意的 Δ z j l \Delta z_j^l Δzjl,让这个神经元的激活值由 σ ( z j l ) \sigma\left(z_{j}^{l}\right) σ(zjl)变为 σ ( z j l + Δ z j l ) \sigma\left(z_{j}^{l} + \Delta z_j^l\right) σ(zjl+Δzjl)。
- 该增量产生的差值会在网络的后续层中传播,最终使得网络的损失函数 C C C增加 ∂ C ∂ z j l Δ z j l \frac{\partial C}{\partial z_{j}^{l}} \Delta z_{j}^{l} ∂zjl∂CΔzjl。
现在,这个恶魔是个好恶魔,他愿意帮助你调整 Δ z j l \Delta z_j^l Δzjl的值来减小损失函数的值。
假设 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^{l}} ∂zjl∂C是一个很大的数(无论正负), Δ z j l \Delta z_{j}^{l} Δzjl可以取与 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^{l}} ∂zjl∂C相反的值使得 C C C的增量 ∂ C ∂ z j l Δ z j l \frac{\partial C}{\partial z_{j}^{l}} \Delta z_{j}^{l} ∂zjl∂CΔzjl为负,从而减小 C C C。
相反,当 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^{l}} ∂zjl∂C接近于0时,那么恶魔也难以通过扰乱加权输入来改善损失函数的值,因为就恶魔而言,神经元已经非常接近最佳了。由此,我们得到一个启发:损失函数 C C C对于神经元加权输入 z j l z^l_j zjl的变化率 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^{l}} ∂zjl∂C可以作为神经元偏离最佳状态的量度,即神经元的误差(error) δ j l \delta_{j}^{l} δjl。
δ j l ≡ ∂ C ∂ z j l \color{red}{\delta_{j}^{l} \equiv \frac{\partial C}{\partial z_{j}^{l}}} δjl≡∂zjl∂C(理解为什么用 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^{l}} ∂zjl∂C作为误差来衡量:上面提到当输入 z j l z_j^l zjl增加任意的 Δ z j l \Delta z_j^l Δzjl时, C C C会增加 ∂ C ∂ z j l Δ z j l \frac{\partial C}{\partial z_{j}^{l}} \Delta z_{j}^{l} ∂zjl∂CΔzjl,故计算出 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^{l}} ∂zjl∂C,就可以使 Δ z j l \Delta z_j^l Δzjl取反,即函数 C C C的增量=(- δ j l \delta_{j}^{l} δjl)^2, C C C减小,导致 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^{l}} ∂zjl∂C减小,如此反复,直至网络达到最佳状态)
由此,我们可以由误差推出反向传播的四个基本方程。
①:输出层的误差向量 δ l \delta^{l} δl
δ j L = ∂ C ∂ a j L σ ′ ( z j L ) \color{red}{\delta_{j}^{L}=\frac{\partial C}{\partial a_{j}^{L}} \sigma^{\prime}\left(z_{j}^{L}\right)} δjL=∂ajL∂Cσ′(zjL)在右侧的第一项 ∂ C ∂ a j L \frac{\partial C}{\partial a_{j}^{L}} ∂ajL∂C表示代价 C C C随神经元的激活输出 a j L a^L_j ajL的变化速率,第二项则表示激活函数 σ \sigma σ对于加权输入 z j L z^L_j zjL的变化速率。
下面把输出层各神经元的误差统写成矩阵形式:
δ L = ∇ a C ⊙ σ ′ ( z L ) \color{red}{\delta^{L}=\nabla_{a} C \odot \sigma^{\prime}\left(z^{L}\right)} δL=∇aC⊙σ′(zL)其中 ∇ a C \nabla_{a} C ∇aC 是一个包含 ∂ C ∂ a j L \frac{\partial C}{\partial a_{j}^{L}} ∂ajL∂C 的向量,当 C C C 为⼆次代价函数时,有 ∇ a C = ( a L − y ) \color{red}{\nabla_{a} C = (a^L -y)} ∇aC=(aL−y) C = 1 2 ∑ j ( y j − a j L ) 2 ∂ C / ∂ a j L = ( a j L − y j ) \begin{aligned} &C=\frac{1}{2} \sum_{j}\left(y_{j}-a_{j}^{L}\right)^{2} \\ &\partial C / \partial a_{j}^{L}=\left(a_{j}^{L}-y_{j}\right) \end{aligned} C=21j∑(yj−ajL)2∂C/∂ajL=(ajL−yj) ② :采用下一层的误差向量 δ l + 1 \delta^{l+1} δl+1表示当前层的误差向量 δ l \delta^l δl
δ l = ( ( w l + 1 ) T δ l + 1 ) ⊙ σ ′ ( z l ) \color{red}{\delta^{l}=\left(\left(w^{l+1}\right)^{T} \delta^{l+1}\right) \odot \sigma^{\prime}\left(z^{l}\right)} δl=((wl+1)Tδl+1)⊙σ′(zl)其中, ( w l + 1 ) T (w^{l+1})^T (wl+1)T 是第 l + 1 l+1 l+1 层权重矩阵的转置
上式旨在用下一层(正向)的误差通过权重矩阵反向(backward )传播到当前层,给出一种通过下层误差计算本层误差的方法。
有了方程①、②,我们可以计算任何层的误差向量,即先计算输出层的误差 δ l \delta^l δl,再递推到前面各层的误差 δ l − 1 \delta^{l-1} δl−1, δ l − 2 \delta^{l-2} δl−2,…。
③ :代价函数对于网络中任一处偏值的变化率
∂ C ∂ b j l = δ j l \color{red}{\frac{\partial C}{\partial b_{j}^{l}} = \delta^l_j} ∂bjl∂C=δjl这是个不错的性质,我们就可以把上式简写成: ∂ C ∂ b = δ \frac{\partial C}{\partial b} = \delta ∂b∂C=δ ④:代价函数对于网络中任一处权重的变化率
∂ C ∂ w j k l = a k l − 1 δ j l \color{red}{\quad \frac{\partial C}{\partial w_{j k}^{l}}=a_{k}^{l-1} \delta_{j}^{l}} ∂wjkl∂C=akl−1δjl可以简记为这种形式: ∂ C ∂ w = a i n δ o u t \quad \frac{\partial C}{\partial w}=a_{in} \delta_{out} ∂w∂C=ainδout这个式子告诉我们,当输入神经元的激活值很低时,会导致权重学习放缓。因为当 a i n a_{in} ain 趋于0时, ∂ C ∂ w \frac{\partial C}{\partial w} ∂w∂C 也会变得很小。
我们还可以从方程①得到一些信息,回忆一下S型(sigmoid)函数的图像,当 σ ( z j L ) \sigma(z^L_j) σ(zjL) 近似为0或1的时候, σ \sigma σ 函数变得很平,这时 σ ′ ( z j L ) ≈ 0 \sigma^{\prime}(z^L_j) ≈ 0 σ′(zjL)≈0 导致 δ j L ≈ 0 \delta^L_j ≈ 0 δjL≈0 。
故对于激活函数为S型函数的输出层神经元,当它处于高激活值或低激活值时,其权重学习缓慢,我们称它已经饱和(saturated)了,类似的结果对于输出层神经元的偏值也是成⽴的。这个性质可以由方程二推广到各层输出神经元。
总结⼀下,我们已经学习到:当输入神经元的激活值很低,或者输出神经元已经达到饱和(激活值过高或过低)时,涉及这些神经元的权重和偏值学习会很缓慢。

5、证明四个基本方程(可选)
我们现在证明这四个基本的⽅程 (BP1)–(BP4)。所有这些都是多元微积分的链式法则的推论。
证明方程①: δ j L = ∂ C ∂ a j L ∂ a j L ∂ z j L a j L = σ ( z j L ) δ j L = ∂ C ∂ a j L σ ′ ( z j L ) \begin{gathered} \delta_{j}^{L}=\frac{\partial C}{\partial a_{j}^{L}} \frac{\partial a_{j}^{L}}{\partial z_{j}^{L}} \\ a_{j}^{L}=\sigma\left(z_{j}^{L}\right) \\ \delta_{j}^{L}=\frac{\partial C}{\partial a_{j}^{L}} \sigma^{\prime}\left(z_{j}^{L}\right) \end{gathered} δjL=∂ajL∂C∂zjL∂ajLajL=σ(zjL)δjL=∂ajL∂Cσ′(zjL)证明方程②:误差通过反向传播,上一层的各神经元的误差都会传入到本层该神经元
δ j l = ∂ C ∂ z j l = ∑ k ∂ C ∂ z k l + 1 ∂ z k l + 1 ∂ z j l = ∑ k ∂ z k l + 1 ∂ z j l δ k l + 1 \begin{aligned} \delta_{j}^{l} &=\frac{\partial C}{\partial z_{j}^{l}} \\ &=\sum_{k} \frac{\partial C}{\partial z_{k}^{l+1}} \frac{\partial z_{k}^{l+1}}{\partial z_{j}^{l}} \\ &=\sum_{k} \frac{\partial z_{k}^{l+1}}{\partial z_{j}^{l}} \delta_{k}^{l+1} \end{aligned} δjl=∂zjl∂C=k∑∂zkl+1∂C∂zjl∂zkl+1=k∑∂zjl∂zkl+1δkl+1
z k l + 1 = ∑ j w k j l + 1 a j l + b k l + 1 = ∑ j w k j l + 1 σ ( z j l ) + b k l + 1 ∂ z k l + 1 ∂ z j l = w k j l + 1 σ ′ ( z j l ) δ j l = ∑ k w k j l + 1 δ k l + 1 σ ′ ( z j l ) \begin{aligned} z_{k}^{l+1}=\sum_{j} w_{k j}^{l+1} a_{j}^{l}+b_{k}^{l+1}=\sum_{j} w_{k j}^{l+1} \sigma\left(z_{j}^{l}\right)+b_{k}^{l+1} \\ \frac{\partial z_{k}^{l+1}}{\partial z_{j}^{l}}=w_{k j}^{l+1} \sigma^{\prime}\left(z_{j}^{l}\right) \\ \delta_{j}^{l}=\sum_{k} w_{k j}^{l+1} \delta_{k}^{l+1} \sigma^{\prime}\left(z_{j}^{l}\right) \end{aligned} zkl+1=j∑wkjl+1ajl+bkl+1=j∑wkjl+1σ(zjl)+bkl+1∂zjl∂zkl+1=wkjl+1σ′(zjl)δjl=k∑wkjl+1δkl+1σ′(zjl)证明方程③: z j l = ∑ k w j k l ⋅ a l − 1 + b j l ∂ C ∂ b j l = ∂ C ∂ z j l ⋅ ∂ z j l ∂ b j l = δ j l \begin{gathered} z_{j}^{l}=\sum_{k} w_{j k}^{l} \cdot a^{l-1}+b_{j}^{l} \\ \frac{\partial C}{\partial b_{j}^{l}}=\frac{\partial C}{\partial z_{j}^{l}} \cdot \frac{\partial z_{j}^{l}}{\partial b_{j}^{l}}=\delta_{j}^{l} \\ \end{gathered} zjl=k∑wjkl⋅al−1+bjl∂bjl∂C=∂zjl∂C⋅∂bjl∂zjl=δjl 证明方程④: z j l = ∑ k w j k l ⋅ a l − 1 + b j l ∂ C ∂ w j k l = ∂ C ∂ z j l ⋅ ∂ z j l ∂ w j k l = δ j l ⋅ a l − 1 \qquad z_{j}^{l}=\sum_{k} w_{j k}^{l} \cdot a^{l-1}+b_{j}^{l} \\ \frac{\partial C}{\partial w_{j k}^{l}}=\frac{\partial C}{\partial z_{j}^{l}} \cdot \frac{\partial z_{j}^{l}}{\partial w_{j k}^{l}}=\delta_{j}^{l} \cdot a^{l-1} zjl=k∑wjkl⋅al−1+bjl∂wjkl∂C=∂zjl∂C⋅∂wjkl∂zjl=δjl⋅al−1
6、反向传播算法
1.输入x:并为输入层设置激活值 a 1 = x a^1 = x a1=x
2.正向传递:对每个层 l = 2 , 3 , . . . , L l = 2,3,...,L l=2,3,...,L计算各层的层输入向量 z l = w l ⋅ a l − 1 + b l z^l = w^l · a^{l-1} + b^l zl=wl⋅al−1+bl和各层输出向量 a l = δ ( z l ) a^l = \delta(z^l) al=δ(zl)
3.输出层误差 δ L \delta^L δL:计算向量 δ L = ∇ a C ⊙ σ ′ ( z L ) \delta^{L}=\nabla_{a} C \odot \sigma^{\prime}\left(z^{L}\right) δL=∇aC⊙σ′(zL)
4.反向传播误差:对每一 l = L − 1 , L − 2 , . . . , 2 l = L-1,L-2,...,2 l=L−1,L−2,...,2,计算 δ l = ( ( w l + 1 ) T δ l + 1 ) ⊙ σ ′ ( z l ) \delta^{l}=\left(\left(w^{l+1}\right)^{T} \delta^{l+1}\right) \odot \sigma^{\prime}\left(z^{l}\right) δl=((wl+1)Tδl+1)⊙σ′(zl)
5.输出代价函数梯度:由误差及方程三和方程四计算代价函数梯度 ∂ C ∂ w j k l = a k l − 1 δ j l \frac{\partial C}{\partial w_{j k}^{l}} = a^{l-1}_k\delta^l_j ∂wjkl∂C=akl−1δjl和 ∂ C ∂ b j l = δ j l \frac{\partial C}{\partial b_{j}^{l}} = \delta^l_j ∂bjl∂C=δjl
在实际中,使用的是最小堆(mini-batch)随机梯度下降法 SGD,每次选定m个训练样本,对每一样本求导数,然后再平均,再应用到梯度下降的表达式中。