- 内网安全攻防:渗透测试实战指南之内网信息搜集
网络安全进阶
渗透测试网络安全渗透测试web安全信息安全
《内网安全攻防:渗透测试实战指南》第2章:内网信息搜集内网渗透测试的核心是信息搜集。本章主要介绍了当前主机信息搜集、域内存活主机探测、域内端口扫描、域内用户和管理员权限的获取、如何获取域内网段划分信息和拓扑架构分析等,并介绍了域分析工具BloodHound的使用。搜集本机信息网络配置信息、操作系统及软件的信息、本机服务信息、进程列表、启动程序信息、计划任务、主机开机时间、用户列表、连接会话、端口列
- 2021年 江南大学研究生考试 算法与程序设计 题目
Bears9
算法数据结构
(2021年江南大学851真题)回忆版,免费供大家学习参考。如有雷同,那人是我室友(室友让我发的)。1、什么是线型结构(8分)删除一个链表的头结点,关键处给出注释(12分)2、题目描述:关于像素点,周围有边界像素,中间是内容像素。从某个内容像素开始上色,依次按右、上、左、下顺时针顺序进行上色。直到将所有的内容像素上色完成什么是栈?(8分)如何用栈的思想完成上色过程?画出图解(12分)3、如何用冒泡
- 华为OD机试E卷 --游戏分组--24年OD统一考试(Java & JS & Python & C & C++)
飞码创造者
最新华为OD机试题库2024华为od游戏javajavascriptc++cpython
文章目录题目描述输入描述输出描述用例题目解析Js算法源码python算法源码java算法源码c++算法源码c算法源码题目描述部门准备举办一场王者荣耀表演赛,有10名游戏爱好者参与,分为两队,每队5人。每位参与者都有一个评分,代表着他的游戏水平。为了表演赛尽可能精彩,我们需要把10名参赛者分为示例尽量相近的两队。一队的实力可以表示为这一队5名队员的评分总和。现在给你10名参与者的游戏水平评分,请你根
- 个体数字化资源的组织方式
圣道寺
日常使用学习方法职场和发展
时间轴组织方式适合活动类素材、会议记录等的序时整理作用:通常可以用于任务材料提交的备份,确定没有用可以删,但是不用太着急,有足够网盘空间的情况下,可以设置一年的最低保存时间(即使看起来没有什么用)。主题、学科、领域的组织方式素材类型,来源渠道的组织方式项目、综合实践性的资源组织形式
- vue3大屏可视化项目,包含地图,各种 图表,全屏适配方案
m0_74825526
javascript开发语言ecmascript
项目设计1.始终满屏适配,这种方案一般用在屏幕变化不会特别的大项目,项目基本上不会用在比例非常不协调的大屏,设计图按1920*1080标准电脑屏幕比,所用的屏幕也基本在这个比例左右2.涉及图表知识点简单,主要有自定义色系,环形图,堆叠柱状图,折线图3.使用高德地图标点做中间地图满屏适配方案实现思路1宽度使用vw,高度使用vh,严格按照设计图换算,并且留出缓冲空间2具体算法,设计图为1920_108
- 超全性能调优标准制定指南,你一定不能错过!
人工智能
0前言我有个朋友说他们国企的系统从未性能调优,功能测试完就上线,线上也没性能问题,何必还做性能调优?本文搞清:为什么要做性能调优?啥时开始做?做性能调优是不是有标准?1为啥做性能调优?有些性能问题是慢慢产生,到了时间就自爆更多性能问题是由访问量波动导致,如活动或公司产品用户量上升也可能一款产品上线后就半死不活,一直没有大访问量,所以还没有引发这颗定时炸弹现在假设你的系统要做一次活动,老板告诉你预计
- 2、Flink 在 DataStream 和 Table 之间进行转换
猫猫爱吃小鱼粮
FlinkSQLflink大数据
1.概述TableAPI和DataStreamAPI都可以处理有界流和无界流。DataStreamAPI提供了流处理的基础(时间、状态和数据流管理);TableAPI抽象了许多内部内容,并提供了一个结构化和声明性的API;在处理历史数据时,需要管理有边界的流;无边界流出现在实时处理场景中,这些场景可能需要先使用历史数据进行初始化。为了高效执行,这两个API都以优化的批处理执行模式处理有界流。由于批
- 家政服务小程序,打造智慧家政新体验
冠品网络科技
小程序小程序开发小程序制作
春节即将来临,家政市场呈现出了火热的场景,大众对家政服务的需求持续增加。近年来,家政市场开始倾向数字化、智能化,借助科学技术打造家政数字化平台,让大众在手机上就可以预约家政服务,减少传统家政市场中繁琐流程。通过家政系统商家可以更好的派单,服务人员也能快速接单,完成工作,提高消费者的家政体验,推动市场创新发展。传统的家政市场需要中介等介绍人对接,用户需要花费大量时间寻找合适的服务人员,过程较为繁琐。
- 空降中层如何做好管理工作?成功过渡的实用策略
空降中层管理公司管理团队管理
空降中层的管理工作充满挑战,既需要迅速适应新环境,又要赢得下属的信任和支持。作为新任的管理者,空降中层不仅要快速理解公司的文化、业务和团队,还要在短时间内建立起有效的领导力和管理体系。做好管理工作可以从以下几个方面着手:快速融入团队、建立信任与沟通、明确目标与期望、优化团队结构、激励与激发团队潜力、以及借助数据与工具进行决策。本文将深入探讨这些管理策略,以帮助空降中层快速适应并实现有效管理。一、快
- 时间轮算法及简易实现
后端算法
一、时间轮算法是什么?1.基本概念时间轮(TimeWheel)是一种高效的定时任务调度算法,用于管理和调度大量的定时任务。它的核心思想是将时间划分为多个槽(Slot),每个槽代表一个时间间隔,任务根据其延迟时间被分配到对应的槽中。时间轮通过一个指针(Pointer)周期性地移动,触发当前槽中的任务执行。2.核心名词解释槽(Slot):时间轮被划分为多个槽,每个槽代表一个时间间隔。例如,一个时间轮有
- Python 中最易误解的功能
前端
有些功能即使是经验丰富的开发者也会被难住。我也曾被它们绊倒,花数小时挠头苦思,最终才学会如何正确应对。所以,不浪费时间,让我们来探索Python中最易误解的功能,它们为何棘手,以及你如何能最终掌握它们。1.可变默认参数问题:如果你曾写过一个带有默认列表或字典参数的函数,你可能会注意到一些奇怪的现象。它会在函数调用之间“记住”值!defadd_item(item,items=[]):items.ap
- 【openGauss】数据库安全-数据库认证机制
小嗑数据库
数据库开源软件
数据库认证机制可获得性本特性自openGauss1.1.0版本开始引入。特性简介提供基于客户端/服务端(C/S)模式的客户端连接认证机制。客户价值加密认证过程中采用单向Hash不可逆加密算法PBKDF2,有效防止彩虹攻击。特性描述openGauss采用基本的客户端连接认证机制,客户端发起连接请求后,由服务端完成信息校验并依据校验结果发送认证所需信息给客户端(认证信息包括盐值、token以及服务端签
- C#语言的数据结构
技术的探险家
包罗万象golang开发语言后端
C#语言的数据结构探讨数据结构是计算机科学中一种用于组织、存储和管理数据的方式。有效地使用数据结构能使算法更加高效,并提高程序的性能。在C#语言中,我们可以构建和使用多种数据结构,以满足不同的需求。本文将介绍C#中的常用数据结构,包括数组、链表、栈、队列、哈希表、树和图等,并探讨它们的特点、实现和应用场景。1.数组数组是一种最基础且常用的数据结构。它是一个固定大小的线性结构,可以通过索引访问其中的
- 机器学习02-发展历史补充
坐吃山猪
机器学习机器学习人工智能
机器学习02-发展历史补充文章目录机器学习02-发展历史补充1-机器学习个人理解1-初始阶段:统计学习和模式识别(20世纪50年代至80年代)2-第二阶段【集成时代】+【核方法】(20世纪90年代至2000年代初期)3-第三阶段【特征工程】+【模型优化】(2000年代中期至2010年代初期)4-大规模数据和分布式计算(2010年代中后期)5-自动化机器学习和特征选择(2010年代末至今)2-神经网
- Java 数组排序
赔罪
Java系统学习java排序算法算法java-ee数组排序
目录1.Java冒泡排序(BubbleSort)1.冒泡排序2.冒泡排序的算法原理3.冒泡排序的复杂度和性能4.形成代码2.Java快速排序(QuickSort)3.Java归并排序(MergeSort)4.Java选择排序(SelectionSort)5.Java直接插入排序6.Java希尔排序(ShellSort)1.Java冒泡排序(BubbleSort)1.冒泡排序冒泡排序(BubbleS
- 麒麟操作系统服务架构保姆级教程(十一)https配置
小屁不止是运维
系统架构架构https网络协议linux运维LNMP服务器
如果你想拥有你从未拥有过的东西,那么你必须去做你从未做过的事情在运维工作中,加密和安全的作用是十分重要的,如果仅仅用http协议来对外展示我们的网站,过一段时间就会发现网站首页被人奇奇怪怪的篡改了,本来好好的博客论坛,被人篡改的五毒俱全,这个时候我们的网站就需要加密访问了,这个加密不是说要密码才可以查看网站,而是通过https协议进行加密访问,客户端进行访问的时候会进行加密和解密,防止我们的web
- 基于SIFT特征提取和模板匹配的车标识别算法MATLAB仿真(含MATLAB代码)
爱学习的通信人
图像处理毕业设计信号处理算法matlab开发语言
摘要本文介绍了一种基于尺度不变特征变换(SIFT)特征提取和模板匹配的车标识别方法,并通过MATLAB进行仿真。该方法利用SIFT特征的尺度和旋转不变性,提高车标识别的准确性和鲁棒性,适用于各种尺寸和方向的车标图像。仿真结果展示了该方法在实际应用中的有效性。关键词:车标识别,SIFT特征提取,模板匹配,MATLAB仿真1.引言车标识别在车辆检测、智能交通系统和安全监控中具有重要应用。准确识别车辆品
- asp.net mysql 性能问题_ASP.NET性能优化小结
syhakh
asp.netmysql性能问题
一、返回多个数据集检查你的访问数据库的代码,看是否存在着要返回多次的请求。每次往返降低了你的应用程序的每秒能够响应请求的次数。通过在单个数据库请求中返回多个结果集,可以减少与数据库通信的时间,使你的系统具有扩展性,也可以减少数据库服务器响应请求的工作量。如果用动态的SQL语句来返回多个数据集,那用存储过程来替代动态的SQL语句会更好些。是否把业务逻辑写到存储过程中,这个有点争议。但是我认为,把业务
- Python 实现七大排序算法
weixin_30527323
pythonshell数据结构与算法
技术博客:github.com/yongxinz/te…本文用Python实现了插入排序、希尔排序、冒泡排序、快速排序、直接选择排序、堆排序、归并排序。先整体看一下各个算法之间的对比,然后再进行详细介绍:排序算法平均时间复杂度最好情况最坏情况空间复杂度排序方式稳定性插入排序O(n²)O(n)O(n²)O(1)In-place稳定冒泡排序O(n²)O(n)O(n²)O(1)In-place稳定选择排
- PCL 点云随机渲染颜色
MelaCandy
PCL点云算法与实战案例3d算法计算机视觉人工智能c++
目录一、概述1.1原理1.2实现步骤1.3应用场景二、代码实现2.1关键函数2.2完整代码三、实现效果PCL点云算法汇总及实战案例汇总的目录地址链接:PCL点云算法与项目实战案例汇总(长期更新)一、概述本文将介绍如何使用PCL库为点云中的每个点随机渲染颜色,并在PCL的可视化窗口中显示。这种方法适用于需要对点云中的不同点进行颜色区分的场景,可以帮助更直观地观察和分析点云数据。1.1原理在点云处理中
- pcl系列-添加自定义点云类型
不会算法的阿召
c++自动驾驶计算机视觉3d
pcl库中附带了各种预定义的点类型,这些数据类型足以支持在pcl中所实现的所有算法和方法,但是在某些情况下,在使用pcl点类型时希望定义新的点类型,比如在LIO-SAM中定义的PointXYZIRPYT(包括点云基本的坐标(x,y,z)和强度I,以及三个旋转角RPY和时间T)。因此,pcl提供了创建自定义点云类型的方法。1.pcl常用点云类型pcl中定义了大量的常用点类型,在定义自己的点类型之前,
- Python数据分析高频面试题及答案
闲人编程
程序员面试python数据分析面试题核心
目录1.基础知识2.数据处理3.数据可视化4.机器学习模型5.进阶问题6.数据清洗与预处理7.数据转换与操作8.时间序列分析9.高级数据分析技术10.数据降维与特征选择11.模型评估与优化12.数据操作与转换13.数据筛选与分析14.数据可视化与报告15.数据统计与分析16.高级数据处理以下是一些Python数据分析的高频核心面试题及其答案,涵盖了基础知识、数据1.基础知识问1:Python中列表
- PCL 生成空间圆点云【2025最新版】
点云侠
PCL学习算法c++3d计算机视觉开发语言
目录一、算法原理二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。博客长期更新,最近一次更新时间为:2025年1月17日。代码在PCL1.14.1中测试通过。一、算法原理 三维空间圆形式如下:三维空间圆的参数方程:{
- Open3D 手动裁剪点云【2025最新版】
点云侠
python点云处理几何学python3d计算机视觉算法
目录一、概述1、主要函数2、基础操作二、代码实现三、结果展示四、相关链接博客长期更新,本文最近更新时间为:2025年1月18日。一、概述 Open3d中的VisualizerWithEditing类提供了图形用户交互功能。draw_geometries_with_editing([pcd])函数提供了顶点选择和裁剪功能。1、主要函数defdraw_geometries_with_editing(
- PCL 点云按曲率大小渲染颜色【2025最新版】
点云侠
PCL学习可视化计算机视觉开发语言3dc++
目录一、表面曲率二、代码实现三、结果展示博客长期更新,本文最近更新时间为:2025年1月6日。一、表面曲率 本案例中,所使用的曲率是指根据点云的特征值计算出来的表面曲率。定义如下:任意一点PPP点的特征值满足
- 数据结构---C++版
海狸_hlz
数据结构数据结构
第1章数据结构的基本概念1.1数据结构在程序设计中的作用1)程序设计的实质是什么?数据表示:将数据存储在计算机(内存)中数据处理:处理数据,设计方案(算法)1.2计算机求解问题:1)问题→抽象出问题的模型→求模型的解问题——数值问题、非数值问题2)数值问题→数学方程非数值问题→数据结构3)本书讨论非数值问题的数据组织和处理,主要内容如下:(1)数据的逻辑结构:线性表、树、图等数据结构,其核心是如何
- 一个非常好用的图片切割工具(c# winform开发)
源之缘-OFD解决方案之道
c#winform
本人业余时间开发了一个图片切割工具,非常好用,也很灵活!特别对大型图片切割,更能体现出该软件的优势!开发工具为winform功能说明可以设定切割的高度和宽度。切割线可以上下拖动,可以增加一个切割区域,可设定某个区域不参与切割。主要技术点分析切割区域确定每个切割区域是一个长方形。用一个结构标识该属性。1classSpliteMoveIndex2{3publicenumEN_DIR4{5NON,6HO
- 随机应变:网站的可扩展性架构
迈克雷(MichaelRay)
架构之美
国内某大型互联网企业经常因为对同行的产品进行微创新,然后推出自己的产品而遭人诟病,不讨论这种做法是否合适,我们分析这些产品,发现大多数都比原创产品有更好的用户体验。这些产品常常后来居上,更速度地推出新功能,吸引用户注意,进而占据市场。微信从发布到拥有1亿用户,仅仅用了一年的时间。而据说摇一摇这个功能是两个实习生用一个星期就开发完成上线的。使用TOP(TaobaoOpenAPI),一个技术熟练的淘宝
- grafana数据库从sqlit3迁移至mysql(tidb)
mark.meng
监控系统数据库grafanamysql
背景grafana默认采用的是sqlite3,由于sqlite3不支持同时写,sqlite的锁是文件锁,作用的是整个DB文件,同一时间可以有多个读事务,但是同一时间最多只能有一个写事务。容易锁库导致grafana报错,现决定将grafana默认sqlite3db文件迁移至mysql(tidb)中。报错信息:Error:databaseislocked迁移步骤1.下载迁移工具镜像dockerpull
- 3.6.树状数组
赵鑫亿
c++数据结构与算法c++算法开发语言数据结构
树状数组基本原理树状数组(BinaryIndexedTree,简称BIT)是一种高效的数据结构,它可以在O(logn)的时间复杂度下实现对数组的单点更新和区间求和操作。前置知识lowbit(intx)函数:计算x的最低位的1及其后面的0组成的数,例如lowbit(6)(二进制为110)等于2(二进制为10)。在树状数组中,i元素的右父节点为i+lowbit(i),左父节点为i-lowbit(i)核
- 异常的核心类Throwable
无量
java源码异常处理exception
java异常的核心是Throwable,其他的如Error和Exception都是继承的这个类 里面有个核心参数是detailMessage,记录异常信息,getMessage核心方法,获取这个参数的值,我们可以自己定义自己的异常类,去继承这个Exception就可以了,方法基本上,用父类的构造方法就OK,所以这么看异常是不是很easy
package com.natsu;
- mongoDB 游标(cursor) 实现分页 迭代
开窍的石头
mongodb
上篇中我们讲了mongoDB 中的查询函数,现在我们讲mongo中如何做分页查询
如何声明一个游标
var mycursor = db.user.find({_id:{$lte:5}});
迭代显示游标数
- MySQL数据库INNODB 表损坏修复处理过程
0624chenhong
tomcatmysql
最近mysql数据库经常死掉,用命令net stop mysql命令也无法停掉,关闭Tomcat的时候,出现Waiting for N instance(s) to be deallocated 信息。查了下,大概就是程序没有对数据库连接释放,导致Connection泄露了。因为用的是开元集成的平台,内部程序也不可能一下子给改掉的,就验证一下咯。启动Tomcat,用户登录系统,用netstat -
- 剖析如何与设计人员沟通
不懂事的小屁孩
工作
最近做图烦死了,不停的改图,改图……。烦,倒不是因为改,而是反反复复的改,人都会死。很多需求人员不知该如何与设计人员沟通,不明白如何使设计人员知道他所要的效果,结果只能是沟通变成了扯淡,改图变成了应付。
那应该如何与设计人员沟通呢?
我认为设计人员与需求人员先天就存在语言障碍。对一个合格的设计人员来说,整天玩的都是点、线、面、配色,哪种构图看起来协调;哪种配色看起来合理心里跟明镜似的,
- qq空间刷评论工具
换个号韩国红果果
JavaScript
var a=document.getElementsByClassName('textinput');
var b=[];
for(var m=0;m<a.length;m++){
if(a[m].getAttribute('placeholder')!=null)
b.push(a[m])
}
var l
- S2SH整合之session
灵静志远
springAOPstrutssession
错误信息:
Caused by: org.springframework.beans.factory.BeanCreationException: Error creating bean with name 'cartService': Scope 'session' is not active for the current thread; consider defining a scoped
- xmp标签
a-john
标签
今天在处理数据的显示上遇到一个问题:
var html = '<li><div class="pl-nr"><span class="user-name">' + user
+ '</span>' + text + '</div></li>';
ulComme
- Ajax的常用技巧(2)---实现Web页面中的级联菜单
aijuans
Ajax
在网络上显示数据,往往只显示数据中的一部分信息,如文章标题,产品名称等。如果浏览器要查看所有信息,只需点击相关链接即可。在web技术中,可以采用级联菜单完成上述操作。根据用户的选择,动态展开,并显示出对应选项子菜单的内容。 在传统的web实现方式中,一般是在页面初始化时动态获取到服务端数据库中对应的所有子菜单中的信息,放置到页面中对应的位置,然后再结合CSS层叠样式表动态控制对应子菜单的显示或者隐
- 天-安-门,好高
atongyeye
情感
我是85后,北漂一族,之前房租1100,因为租房合同到期,再续,房租就要涨150。最近网上新闻,地铁也要涨价。算了一下,涨价之后,每次坐地铁由原来2块变成6块。仅坐地铁费用,一个月就要涨200。内心苦痛。
晚上躺在床上一个人想了很久,很久。
我生在农
- android 动画
百合不是茶
android透明度平移缩放旋转
android的动画有两种 tween动画和Frame动画
tween动画;,透明度,缩放,旋转,平移效果
Animation 动画
AlphaAnimation 渐变透明度
RotateAnimation 画面旋转
ScaleAnimation 渐变尺寸缩放
TranslateAnimation 位置移动
Animation
- 查看本机网络信息的cmd脚本
bijian1013
cmd
@echo 您的用户名是:%USERDOMAIN%\%username%>"%userprofile%\网络参数.txt"
@echo 您的机器名是:%COMPUTERNAME%>>"%userprofile%\网络参数.txt"
@echo ___________________>>"%userprofile%\
- plsql 清除登录过的用户
征客丶
plsql
tools---preferences----logon history---history 把你想要删除的删除
--------------------------------------------------------------------
若有其他凝问或文中有错误,请及时向我指出,
我好及时改正,同时也让我们一起进步。
email : binary_spac
- 【Pig一】Pig入门
bit1129
pig
Pig安装
1.下载pig
wget http://mirror.bit.edu.cn/apache/pig/pig-0.14.0/pig-0.14.0.tar.gz
2. 解压配置环境变量
如果Pig使用Map/Reduce模式,那么需要在环境变量中,配置HADOOP_HOME环境变量
expor
- Java 线程同步几种方式
BlueSkator
volatilesynchronizedThredLocalReenTranLockConcurrent
为何要使用同步? java允许多线程并发控制,当多个线程同时操作一个可共享的资源变量时(如数据的增删改查), 将会导致数据不准确,相互之间产生冲突,因此加入同步锁以避免在该线程没有完成操作之前,被其他线程的调用, 从而保证了该变量的唯一性和准确性。 1.同步方法&
- StringUtils判断字符串是否为空的方法(转帖)
BreakingBad
nullStringUtils“”
转帖地址:http://www.cnblogs.com/shangxiaofei/p/4313111.html
public static boolean isEmpty(String str)
判断某字符串是否为空,为空的标准是 str==
null
或 str.length()==
0
- 编程之美-分层遍历二叉树
bylijinnan
java数据结构算法编程之美
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class LevelTraverseBinaryTree {
/**
* 编程之美 分层遍历二叉树
* 之前已经用队列实现过二叉树的层次遍历,但这次要求输出换行,因此要
- jquery取值和ajax提交复习记录
chengxuyuancsdn
jquery取值ajax提交
// 取值
// alert($("input[name='username']").val());
// alert($("input[name='password']").val());
// alert($("input[name='sex']:checked").val());
// alert($("
- 推荐国产工作流引擎嵌入式公式语法解析器-IK Expression
comsci
java应用服务器工作Excel嵌入式
这个开源软件包是国内的一位高手自行研制开发的,正如他所说的一样,我觉得它可以使一个工作流引擎上一个台阶。。。。。。欢迎大家使用,并提出意见和建议。。。
----------转帖---------------------------------------------------
IK Expression是一个开源的(OpenSource),可扩展的(Extensible),基于java语言
- 关于系统中使用多个PropertyPlaceholderConfigurer的配置及PropertyOverrideConfigurer
daizj
spring
1、PropertyPlaceholderConfigurer
Spring中PropertyPlaceholderConfigurer这个类,它是用来解析Java Properties属性文件值,并提供在spring配置期间替换使用属性值。接下来让我们逐渐的深入其配置。
基本的使用方法是:(1)
<bean id="propertyConfigurerForWZ&q
- 二叉树:二叉搜索树
dieslrae
二叉树
所谓二叉树,就是一个节点最多只能有两个子节点,而二叉搜索树就是一个经典并简单的二叉树.规则是一个节点的左子节点一定比自己小,右子节点一定大于等于自己(当然也可以反过来).在树基本平衡的时候插入,搜索和删除速度都很快,时间复杂度为O(logN).但是,如果插入的是有序的数据,那效率就会变成O(N),在这个时候,树其实变成了一个链表.
tree代码:
- C语言字符串函数大全
dcj3sjt126com
cfunction
C语言字符串函数大全
函数名: stpcpy
功 能: 拷贝一个字符串到另一个
用 法: char *stpcpy(char *destin, char *source);
程序例:
#include <stdio.h>
#include <string.h>
int main
- 友盟统计页面技巧
dcj3sjt126com
技巧
在基类调用就可以了, 基类ViewController示例代码
-(void)viewWillAppear:(BOOL)animated
{
[super viewWillAppear:animated];
[MobClick beginLogPageView:[NSString stringWithFormat:@"%@",self.class]];
- window下在同一台机器上安装多个版本jdk,修改环境变量不生效问题处理办法
flyvszhb
javajdk
window下在同一台机器上安装多个版本jdk,修改环境变量不生效问题处理办法
本机已经安装了jdk1.7,而比较早期的项目需要依赖jdk1.6,于是同时在本机安装了jdk1.6和jdk1.7.
安装jdk1.6前,执行java -version得到
C:\Users\liuxiang2>java -version
java version "1.7.0_21&quo
- Java在创建子类对象的同时会不会创建父类对象
happyqing
java创建子类对象父类对象
1.在thingking in java 的第四版第六章中明确的说了,子类对象中封装了父类对象,
2."When you create an object of the derived class, it contains within it a subobject of the base class. This subobject is the sam
- 跟我学spring3 目录贴及电子书下载
jinnianshilongnian
spring
一、《跟我学spring3》电子书下载地址:
《跟我学spring3》 (1-7 和 8-13) http://jinnianshilongnian.iteye.com/blog/pdf
跟我学spring3系列 word原版 下载
二、
源代码下载
最新依
- 第12章 Ajax(上)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- BI and EIM 4.0 at a glance
blueoxygen
BO
http://www.sap.com/corporate-en/press.epx?PressID=14787
有机会研究下EIM家族的两个新产品~~~~
New features of the 4.0 releases of BI and EIM solutions include:
Real-time in-memory computing –
- Java线程中yield与join方法的区别
tomcat_oracle
java
长期以来,多线程问题颇为受到面试官的青睐。虽然我个人认为我们当中很少有人能真正获得机会开发复杂的多线程应用(在过去的七年中,我得到了一个机会),但是理解多线程对增加你的信心很有用。之前,我讨论了一个wait()和sleep()方法区别的问题,这一次,我将会讨论join()和yield()方法的区别。坦白的说,实际上我并没有用过其中任何一个方法,所以,如果你感觉有不恰当的地方,请提出讨论。
&nb
- android Manifest.xml选项
阿尔萨斯
Manifest
结构
继承关系
public final class Manifest extends Objectjava.lang.Objectandroid.Manifest
内部类
class Manifest.permission权限
class Manifest.permission_group权限组
构造函数
public Manifest () 详细 androi
- Oracle实现类split函数的方
zhaoshijie
oracle
关键字:Oracle实现类split函数的方
项目里需要保存结构数据,批量传到后他进行保存,为了减小数据量,子集拼装的格式,使用存储过程进行保存。保存的过程中需要对数据解析。但是oracle没有Java中split类似的函数。从网上找了一个,也补全了一下。
CREATE OR REPLACE TYPE t_split_100 IS TABLE OF VARCHAR2(100);
cr
其中M是整数
,记做

,记做
即实部为偶函数
即虚部为奇函数
即实部是奇函数
即虚部是偶函数
![]() 的FT具有共轭对称性;序列x(n)的
的FT具有共轭对称性;序列x(n)的![]() 具有共轭反对称性,即:
具有共轭反对称性,即:![]() 的FT是
的FT是![]() 的实部
的实部![]() ;序列x(n)的共轭反对称部分
;序列x(n)的共轭反对称部分![]() 的FT是
的FT是![]() ,即:
,即:


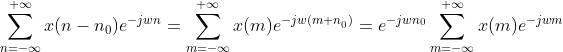
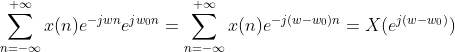
![\sum_{n=-\infty }^{+\infty }x^{*}(-n)e^{-jwn}=[\sum_{n=-\infty }^{+\infty }x(-n)e^{jwn}]^{*}=[\sum_{m=+\infty }^{-\infty }x(m)e^{-jwm}]^{*}=X^{*}(e^{jw})](http://img.e-com-net.com/image/info8/efeaac3195c84b63be2cacb126448a10.gif)
![\sum_{n=-\infty }^{+\infty }x^{*}(n)e^{-jwn}=[\sum_{n=-\infty }^{+\infty }x(n)e^{jwn}]^{*}=[\sum_{n=-\infty }^{+\infty }x(n)e^{-j(-w)n}]^{*}=X^{*}(e^{-jw})](http://img.e-com-net.com/image/info8/b1377b3271fb4fdbb4a5cb0ea38a66e8.gif)