八数码问题的A搜索
这个代码实现的是《人工智能》(第四版)p125
主要思想:
1.八数码空格在不超出范围且不移回上一步状态,便可有上移,下移,左移,右移几种可能的情况。
2.将当前八数码情况与目标状态比较选出“不在位”的最小数码。作为最优状态,继续扩展。(不算当前八数码空格位置)
例如下图,S为初始状态的八数码,S1为S空格上移,Sg为目标状态。
其“不在位”数量分别为 4, 3,所以S1会被选为最优状态
from copy import*
dic = {} #存储移动可能的结果
cou = 0 #给不同状态八数码标一个号,区分
h = 0 #深度
tg = [[1, 2, 3], [8, 0, 4], [7, 6, 5]]
def Now_status(status): #打印出当前状态 # #208,163,754
for m in status: #{1: [[[0, 2, 8], [1, 6, 3], [7, 5, 4]], 'left'], 2: [[[2, 8, 0], [1, 6, 3], [7, 5, 4]], 'right']}
for n in m:
print(n, end = " " )
print(end = "\n")
def getIndex(a,value): #获得空格的位置
for i in range(len(a)):
for j in range(len(a[i])):
if a[i][j] == value:
m,n = i,j
return m,n
def left(m,n,a,flag):
global cou
if n-1 >= 0 and flag != "right": #左移 之前右移不可能再左移回去
flag = "left"
cou += 1
a[m][n], a[m][n - 1] = a[m][n - 1], a[m][n]
dic[cou] = [a,flag]
def right(m,n,a,flag):
global cou
if n+1 < len((a[m])) and flag != "left": #右移
flag = "right"
cou += 1
a[m][n], a[m][n + 1] = a[m][n + 1], a[m][n]
dic[cou] = [a, flag]
def up(m,n,a,flag):
global cou
if m-1 >= 0 and flag != "down" :
flag = "up"
cou += 1
a[m][n], a[m - 1][n] = a[m - 1][n], a[m][n]
dic[cou] = [a, flag]
def down(m,n,a,flag):
global cou
if m+1 < len(a) and flag != "up":
flag = "down"
cou += 1
a[m][n], a[m + 1][n] = a[m + 1][n], a[m][n]
dic[cou] = [a, flag]
def move(a, flag):
b = deepcopy(a) #a改变一个值,然后全都会变的
c = deepcopy(a)
d = deepcopy(a)
m, n = getIndex(a, 0)
left(m, n, a, flag)
right(m, n, b, flag)
up(m, n, c, flag)
down(m, n, d, flag)
def input_Now_status():
for m,n in zip(dic.keys(),(dic.values())):
print("情况为:",n[1])
Now_status(n[0])
def input_Ele(): #输入初始八数码,目标状态八数码在一开始定义了的
a = []
x = 0
while x < 3:
x = x+1
print("请输入第",x,"行(请以逗号分隔):")
Ele = input()
Ele = Ele.split(",")
if len(Ele) == 3:
a.append(list(map(int, Ele))) #因为输入的一串是字符串,这里是为int
else:
print("所输入的列数不正确,请重新输入")
x = x - 1
return a
选出扩展最优的八数码状态
def compare(): #与目标相比,选出最优
dic_s = {} #存储不在目标值的数量
for key,values in zip (dic.keys(),dic.values()): #与目标相比
m = 0
value = values[0]
for i in range(len(value)):
for j in range(len(value[i])):
if value[i][j] != tg[i][j] and value[i][j] != 0:
m += 1
dic_s[key] = m
best_value = (sorted(dic_s.items(), key=lambda d:d[1])[0])[1]
for key,value in zip (dic_s.keys(),dic_s.values()): #选出最优
if best_value < value:
del dic[key]
else:
best_value = value
best_key = key
print("最优为",end="")
input_Now_status()
return dic_s[best_key] #返回最优不在目标状态的数量
def tg_end(a): #循环,直达变为目标状态,flag
global h
flag = ""
move(a, flag)
h += 1
print("第",h,"层:")
m = compare()
while m > 0:
dic_change = dic.copy() # 存储改变过的字典
for key, value in zip(dic_change.keys(), dic_change.values()): # 可能有多个最优情况,需要例举出可能的情况,再做比较
move(value[0], value[1])
del dic[key] # 移动过的八数码,接下来会被删除
h += 1
print("第",h,"层:")
m = compare()
print("结束!!!")
主函数
def main():
print("******Welcome to the 八数码******") #a = [[2, 8, 3], [1, 6, 4], [7, 0, 5]]
a = input_Ele() # 2,8,3 1,6,4 7,0,5
print("开始状态")
Now_status(a)
tg_end(a)
效果图

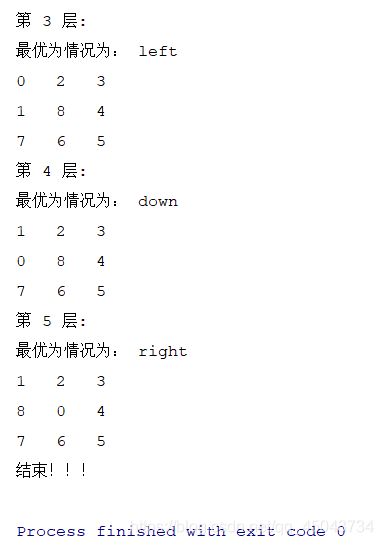
启发信息给得越多即估计函数值越大,则A算法需要搜索处理的状态数就越少,其效率就越高。但也不是估价函数值越大越好,因为估价函数值太大会使A算法不一定能搜索到最优解。例如p130页课后习题的[[2,0,8],[1,6,3],[7,5,4]]要是用上面的代码就陷入死循环了。所以A*就诞生了熬。
第一次写这个,多多指教啦_
