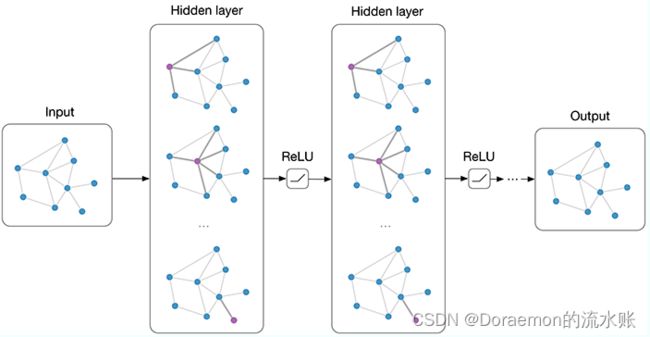
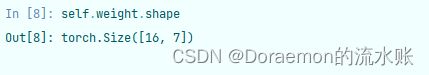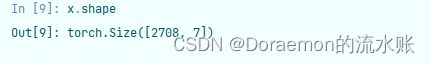GCN源码分析——从DEBUG走起
上次分析完GAT的源码之后,对图神经模型的代码实现有了一定的了解。《GAT源码分析——从DEBUG走起》![]() https://blog.csdn.net/weixin_41724843/article/details/127939516
https://blog.csdn.net/weixin_41724843/article/details/127939516
今天继续看GCN,从图卷积的角度看代码的实现。
前置工作
代码结构树
pygcn
├── data
│ └── cora
│ ├── README
│ ├── cora.cites
│ └── cora.content
├── pygcn
│ ├── __init__.py
│ ├── layers.py
│ ├── models.py
│ ├── train.py
│ └── utils.py
├── LICENCE
├── README.md
├── __init__.py
├── figure.png
└── setup.py
Cora数据集简介
cora.content中包含了七类机器学习的论文,共计2708行,每行以ID起始,中间是1433维的one-hot特征,最后一列是对应的类别
cora.cites中每一行由两个数字构成,第一个数字代表被引用论文的ID。第二个数字代表引用前面论文的那篇论文的ID
加载数据
在load_data后下断,查看加载的数据内容
adj为归一化后的邻接矩阵,features表示了2708篇文章的1433维特征,labels是这些文章对应的标签,idx_train,idx_val,idx_test分别表示了文章节点的训练集测试集与验证集的索引划分。
跟进load_data,里面有三个细节说一下
# build symmetric adjacency matrix,计算转置矩阵。将有向图转成无向图
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
features = normalize(features) # 对特征做了归一化的操作
adj = normalize(adj + sp.eye(adj.shape[0])) # 对A+I归一化第一个细节是adj自身加上一个转置矩阵,用来实现有向图到无向图的转化,因为这里面使用的是GCN模型,GCN中频域卷积使用拉普拉斯矩阵只能处理无向图,文中是这样说明的
第二个细节是特征矩阵的归一化,最开始,特征矩阵每行数值之和是这样的:
为了使其每行数值之和为1,先将数值和取倒数,同时将无穷大置为0,接着构建了如下图的对角矩阵。
可以看到第一个0.05就是第一行数值和(20)的倒数,最后通过点乘原特征矩阵实现归一化。
第三个细节就是邻接矩阵的归一化,因为论文中有公式:
其中H为特征矩阵,W为可学习的参数,A~矩阵就是要做的归一化的邻接矩阵。
那么,为什么要做归一化呢?
因为采用加法规则的时候,度越大的节点特征也会越来越大,度小的节点正好相反,就有可能会导致网络训练中出现的梯度爆炸与梯度消失。
因此,邻接矩阵加上单位阵,归一化来完成
adj = normalize(adj + sp.eye(adj.shape[0])) # 对A+I归一化源码这里是使用了简单的归一化方法。
模型定义
model = GCN(nfeat=features.shape[1],
nhid=args.hidden,
nclass=labels.max().item() + 1,
dropout=args.dropout)跟进GCN
class GCN(nn.Module):
def __init__(self, nfeat, nhid, nclass, dropout):
super(GCN, self).__init__()
self.gc1 = GraphConvolution(nfeat, nhid) # 构建第一层 GCN
self.gc2 = GraphConvolution(nhid, nclass) # 构建第二层 GCN
self.dropout = dropout
def forward(self, x, adj):
x = F.relu(self.gc1(x, adj))
x = F.dropout(x, self.dropout, training=self.training)
x = self.gc2(x, adj)
return F.log_softmax(x, dim=1)构建第一层
nfeat为初始特征,nhid为隐藏层特征,跟进GraphConvolution(nfeat, nhid)
def __init__(self, in_features, out_features, bias=True):
super(GraphConvolution, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.FloatTensor(in_features, out_features)) # input_features, out_features
if bias:
self.bias = Parameter(torch.FloatTensor(out_features))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self):
stdv = 1. / math.sqrt(self.weight.size(1))
self.weight.data.uniform_(-stdv, stdv) # 随机化参数
if self.bias is not None:
self.bias.data.uniform_(-stdv, stdv)不难看出,根据in_features和out_features构造出了weight的参数,以及对bias的构造,然后是reset_parameters方法的参数随机化,这就是第一层。
构建第二层
在第二层中,输入是隐层的维度,输出的是和多分类类别数是一样的。其他部分同第一层
模型训练
def train(epoch):
t = time.time()
model.train()
optimizer.zero_grad() # GraphConvolution forward
output = model(features, adj) # 运行模型,输入参数 (features, adj)
loss_train = F.nll_loss(output[idx_train], labels[idx_train])
acc_train = accuracy(output[idx_train], labels[idx_train])
loss_train.backward()
optimizer.step()optimizer.zero_grad()梯度置零后,将参数输入到模型中
进入第一层,看到了:
def forward(self, input, adj):
support = torch.mm(input, self.weight) # GraphConvolution forward。input*weight
output = torch.spmm(adj, support) # 稀疏矩阵的相乘,和mm一样的效果
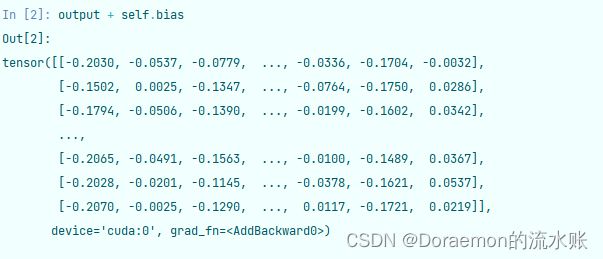
if self.bias is not None:
return output + self.bias
else:
return output先是input和weight相乘,也就是特征矩阵和权重参数相乘,再和邻接矩阵相乘(这里面用了spmm做相乘是因为adj是稀疏矩阵),加偏置,这也就是第一层,看一下输出:
来到第二层,这个时候self.weight已经变了
过第两层之后,输出的矩阵维度
也就是
output = F.log_softmax(x, dim=1)然后再
loss_train = F.nll_loss(output[idx_train], labels[idx_train])最后计算准确率
def accuracy(output, labels):
preds = output.max(1)[1].type_as(labels)
correct = preds.eq(labels).double()
correct = correct.sum()
return correct / len(labels)完成,水水的一篇。
个人感觉GCN主要还是难在推导上,数学好难,菜狗溜了
参考:
GCN笔记-GCN有向图无向图问题_码匀的博客-CSDN博客