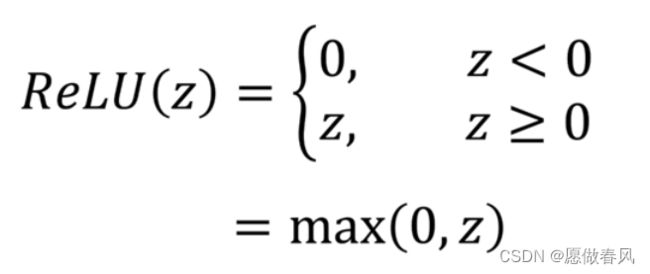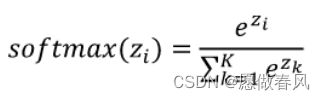神经网络学习问题

神经网络学习问题

1. 神经网络为什么要使用激活函数，而且激活函数不能使用线性函数？

如果不使用用激活函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（f(x)=wx+b）。如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。详细内容见https://blog.csdn.net/Fhujinwu/article/details/108665953

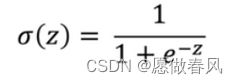
常见的激活函数有：

• sigmoid函数:
  
  下面展示一些 sigmoid函数代码。

def sigmoid(x):
    return 1 / (1 + np.exp(-x))  

• Relu函数：
  
  下面展示一些 Relu。

# ReLU函数
def relu(x):
    return np.maximum(0, x)

• softmax函数：
  

下面展示一些 softmax函数。

def softmax(z):
    c = np.max(z)
    exp_z = np.exp(z - c) # 溢出对策
    sum_exp_z = np.sum(exp_z)
    y = exp_z / sum_exp_z
    
    return y

2.为什么不能使用单个神经元，而要使用多层的神经网络？

单个神经元是一种线性划分输入数据的模型，只能产生线性决策边界，适用于二分类问题；而多层的神经网络的适用范围更为广泛。

3. 什么梯度？什么是梯度消失，梯度爆炸？

• 梯度：梯度可以定义为一个函数的全部偏导数构成的向量，可以表示某一函数在某点处沿该点方向导数取得最大值的方向
• 梯度消失：在反向传播的过程中，需要对激活函数进行求导，当导数小于1，那么随着网络层数的增加梯度更新信息会朝着指数衰减的方式减少，这就是梯度消失。例如sigmoid函数的导数最大为0.25，且大部分数值都被推向两侧饱和区域，这就导致大部分数值经过sigmoid激活函数之后，其导数都非常小，多个小于等于0.25的数值相乘，其运算结果很小
  解决方案：可以考虑用ReLU激活函数取代sigmoid激活函数
• 梯度爆炸：与梯度消失相反，导数大于1，那么会随着网络层数的增加梯度更新将会朝着指数爆炸的方式增加，这就是梯度爆炸

下面展示 随机梯度下降代码。

# 求单点的梯度（no_batch）
def _numerical_gradient_no_batch(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)# 生成和x形状相同的数组
    
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)的计算
        
        x[idx] = tmp_val - h 
        fxh2 = f(x)  # f(x-h)的计算
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val  # 还原值
        
    return grad

下面展示 小批量代码。

# 求一组点的梯度（batch）
def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad

# 示例函数
def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1) # 如果 x 是长度为2的向量，那么f(x) = x1**2 + x2**2

# 画图函数
def tangent_line(f, x):
    k = numerical_gradient(f, x)
    print(k)
    b = f(x) - k*x
    return lambda t: k*t + b

# 开始画图
x0 = np.arange(-2, 2.5, 0.25)
x1 = np.arange(-2, 2.5, 0.25)
X, Y = np.meshgrid(x0, x1)

X = X.flatten()
Y = Y.flatten()

grad = numerical_gradient(function_2, np.array([X, Y]))

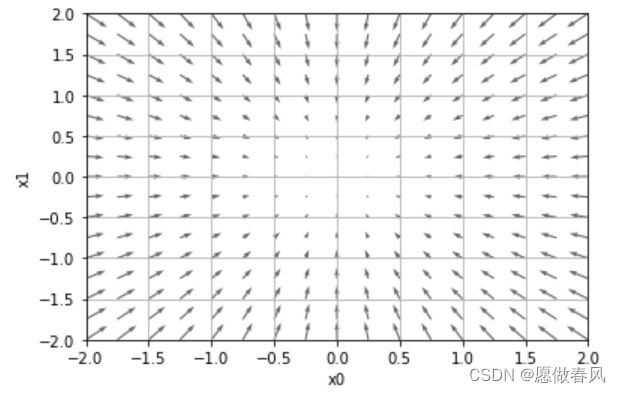
plt.figure()
plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.legend()
plt.draw()
plt.show()

下面展示一些 梯度下降法代码。

# 梯度下降法
def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x, np.array(x_history)

# 示例函数
def function_2(x):
    return x[0]**2 + x[1]**2

# 初始点
init_x = np.array([-3.0, 4.0])    

# 学习率和重复次数
lr = 0.1
step_num = 100

# 开始计算
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
print("x最终值：", x)
# print("x计算过程：\n", x_history)

4.学习速率的作用是什么？

学习速率控制着权重修正量的步长，值越小，沿着向下的斜率就越慢，权重修正花费时间越长，过拟合；值越大，损失函数不收敛，欠拟合。

5.训练神经网络的主要过程是什么？

• 1）选择激活函数
• 2）对权重/偏置量进行初始化，定义神经网络的结构和前向传播的输出结果。
• 3）定义损失函数以及选择反向传播优化的算法
• 4）反复修正权重，直至到达最优，其值不在变化。
  

6. 什么是epoch？为什么要训练多个epoch？

epoch:代，对所有训练数据遍历一遍，即当一个完整的数据集通过了神经网络一次并且返回了一次，这个过程称为一次epoch。然而，当一个epoch对于计算机而言太庞大的时候，就需要把它分成多个小块。
训练多个epoch原因：在训练时，将所有数据迭代训练一次是不够的，需要反复多次才能拟合收敛。随着epoch数量的增加，神经网络中权重更新迭代的次数增多，曲线从最开始的不拟合状态，慢慢进入优化拟合状态，最终进入过拟合。因此，epoch的个数是非常重要的。

7. 神经网络的更新方式有哪几种，各自的更新频率如何？各有什么优缺点？

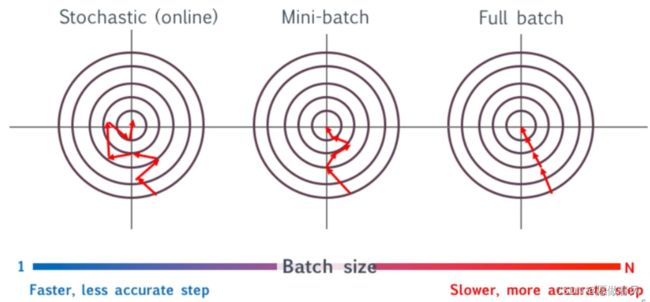
• 1）随机梯度下降：更新之前使用单条数据计算梯度，每代调整n步（n=训练集大小）
• 2）小批量：更新之前使用小部分数据（比单数据多）计算梯度，每代调整m步（m=n/批数据量）
• 3）梯度下降（全批量）：更新之前使用整数据集计算梯度，每代调整一步
  

8.Dropout的作用是什么？

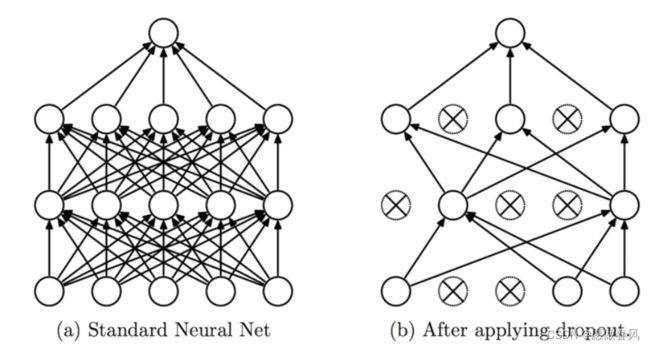
Dropout:随机删除网络中的一些隐藏神经元，保持输入输出神经元不变；
目的：防止神经网络过渡依赖网络中的部分个体，有效地减轻过拟合的发生，使得网络更加健壮。

9. 什么是Keras？

Keras中文文档中的定义：

Keras是一个模型库，是为开发深度学习模型提供了高层次的构建模块。它不处理诸如张量乘积和卷积等低级操作。相反，它依赖于一个专门的、优化的张量操作库来完成这个操作，它可以作为 Keras 的「后端引擎」。相比单独地选择一个张量库，而将 Keras 的实现与该库相关联，Keras 以模块方式处理这个问题，并且可以将几个不同的后端引擎无缝嵌入到 Keras 中。
简单来说，Keras就是一个包含各种各样深度学习模型并且方便调用的库，通过接口你便可以构造想要的模型，这也就是定义中高层次的意思：你不需要去深入了解怎么实现，只需要去调用即可。同样，高度封装也就意味着灵活性欠缺，你没法像使用TensorFlow那样深入底层，去修改调整甚至创造属于自己的模型。最简单的模型是Sequential 顺序模型
下面展示一些 Sequential 顺序模型码片。

from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
model_1 = Sequential()
model_1.add(Dense(64, activation='relu', input_shape=(784,)))
model_1.add(Dropout(0.2))
model_1.add(Dense(64, activation='relu'))
model_1.add(Dropout(0.2))
model_1.add(Dense(10, activation='softmax'))
learning_rate = .001
#在完成了模型的构建后, 可以使用.compile() 来配置学习过程
model_1.compile(loss='categorical_crossentropy',
              optimizer=RMSprop(lr=learning_rate),
              metrics=['accuracy'])

#批量地在训练数据上进行迭代了：        
batch_size = 128  # mini-batch with 128 examples
epochs = 30
history = model_1.fit(
    x_train, y_train,
    batch_size=batch_size,
    epochs=epochs,
    verbose=1,
    validation_data=(x_test, y_test))
#评估模型性能：
score = model_1.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

10.什么是超参数？

超参数是指能人工指定的参数。
在神经网络中，超参数有：

1. 学习率 ；
2. 神经网络的层数 ；
3. 每一个隐层中神经元的个数 ；
4. 学习的回合数Epoch；
5. batch_size 的大小；
6. 损失函数的选择；
7. 权重初始化的方法；
8. 神经元激活函数的类型；

11. 影响一个神经网络模型性能的因素有哪些？

1. 样本数量
2. 网络结构：隐藏层数量以及每层的神经元的数量
3. 学习率
4. 训练集和测试集的划分比例（交叉验证）
5. epoch的大小
6. Bachsize的大小
7. 优化器的选择（？）
8. 损失函数选择
9. 激活函数的选择
10. Dropout的比例