吴恩达机器学习logistic回归作业（python实现）

1. Logistic regression

在这部分的练习中，你将建立一个逻辑回归模型来预测一个学生是否能进入大学。假设你是一所大学的行政管理人员，你想根据两门考试的结果，来决定每个申请人是否被录取。你有以前申请人的历史数据，可以将其用作逻辑回归训练集。对于每一个训练样本，你有申请人两次测评的分数以及录取的结果。为了完成这个预测任务，我们准备构建一个可以基于两次测试评分来评估录取可能性的分类模型。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt

# ------------sigmiod函数-------------
def sigmoid(z):
    return 1 / (1 + np.exp(- z))

# -----------代价函数-----------------
def cost(theta, X, y):
    first = (-y) * np.log(sigmoid(X @ theta))     #cost函数前面的项  @是矩阵乘法
    second = (1 - y)*np.log(1 - sigmoid(X @ theta))   #cost函数后面的项
    return np.mean(first - second)  # 求均值
#------------梯度计算--------------
def gradient(theta, X, y):
    return (X.T @ (sigmoid(X @ theta) - y))/len(X)
#------------模型预测函数--------------
def predict(theta, X):
    probability = sigmoid(X@theta)
    return [1 if x >= 0.5 else 0 for x in probability]  # return a list

# --------------1.读取数据 数据可视化-----------------
data = pd.read_csv('ex2data1.txt', names=['exam1', 'exam2', 'admitted'])  # 读入数据 标记列名
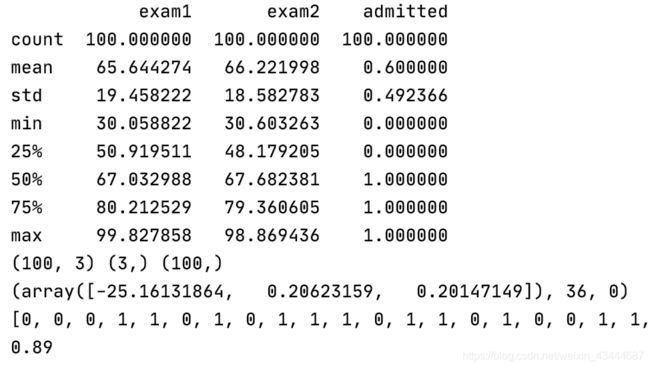
print (data.describe())   # 计算基本信息
positive = data[data.admitted.isin(['1'])]  # 挑选出admitted列中值为1的数据
negetive = data[data.admitted.isin(['0'])]  # 挑选出admitted列中值为0的数据

fig, ax = plt.subplots(figsize=(6,5))   # 1行1个6*5大小的图
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')   #画散点图，x y 点的颜色 标签
ax.scatter(negetive['exam1'], negetive['exam2'], s=50, c='r', marker='x', label='Not Admitted')  #画散点图，x y 点的颜色 点的形状 标签
ax.legend(loc='center left', bbox_to_anchor=(0.2, 1.12),ncol=3)  # 设置图例显示在图的上方
ax.set_xlabel('Exam 1 Score')  # 设置横坐标名
ax.set_ylabel('Exam 2 Score')  # 设置纵坐标名
plt.show()

# ---------------2.数据预处理-----------------
if 'Ones' not in data.columns:
    data.insert(0, 'Ones', 1)         # 在data中加一列x0

X = data.iloc[:, :-1].values  # x0，x1，x2
y = data.iloc[:, -1].values  # 最后一列 admitted
theta = np.zeros(X.shape[1])    #设定theta初始值为0
print (X.shape, theta.shape, y.shape)    #检查矩阵维度

# ---------------3.利用优化的梯度下降算法求解-----------------
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))   #func:优化的目标函数  fprime：梯度函数 args：数据 x0 初值
print (result)

# ---------------4.模型预测-----------------
final_theta = result[0]      # 0里面存的是最终的theta值
predictions = predict(final_theta, X)    #计算预测值
print(predictions)
correct = [1 if a==b else 0 for (a, b) in zip(predictions, y)]   #检查预测值和真实值的偏差，相等为1，不等为0
accuracy = sum(correct) / len(X)
print (accuracy)
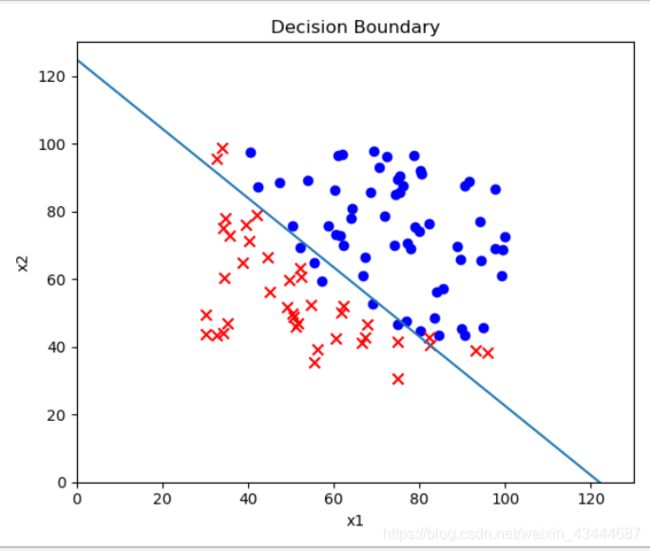
# ---------------5.决策边界-----------------
x1 = np.arange(130, step=0.1)
x2 = -(final_theta[0] + x1*final_theta[1]) / final_theta[2]
fig, ax = plt.subplots(figsize=(6,5))
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')
ax.scatter(negetive['exam1'], negetive['exam2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x1, x2)
ax.set_xlim(0, 130)
ax.set_ylim(0, 130)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_title('Decision Boundary')
plt.show()

2. Regularized logistic regression

在训练的第二部分，我们将要通过加入正则项提升逻辑回归算法。简而言之，正则化是成本函数中的一个术语，它使算法更倾向于“更简单”的模型（在这种情况下，模型将更小的系数）。这个理论助于减少过拟合，提高模型的泛化能力。这样，我们开始吧。

设想你是工厂的生产主管，你有一些芯片在两次测试中的测试结果。对于这两次测试，你想决定是否芯片要被接受或抛弃。为了帮助你做出艰难的决定，你拥有过去芯片的测试数据集，从其中你可以构建一个逻辑回归模型。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
# ------------sigmiod函数-------------
def sigmoid(z):
    return 1 / (1 + np.exp(- z))
# -----------代价函数-----------------
def cost(theta, X, y):
    first = (-y) * np.log(sigmoid(X @ theta))  # cost函数前面的项  @是矩阵乘法
    second = (1 - y) * np.log(1 - sigmoid(X @ theta))  # cost函数后面的项
    return np.mean(first - second)  # 求均值
# ------------梯度计算--------------
def gradient(theta, X, y):
    return (X.T @ (sigmoid(X @ theta) - y)) / len(X)
# ------------模型预测函数--------------
def predict(theta, X):
    probability = sigmoid(X @ theta)
    return [1 if x >= 0.5 else 0 for x in probability]  # return a list
# ------------数据可视化---------------
def plot_data():
    positive = data2[data2['Accepted'].isin([1])]
    negative = data2[data2['Accepted'].isin([0])]

    fig, ax = plt.subplots(figsize=(8, 5))
    ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
    ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
    ax.legend()
    ax.set_xlabel('Test 1 Score')
    ax.set_ylabel('Test 2 Score')

# -------------数据不符合线性逻辑回归，因此要增加特征-----------
def feature_mapping(x1, x2, power):
    data = {}
    for i in np.arange(power + 1):
        for p in np.arange(i + 1):
            data["f{}{}".format(i - p, p)] = np.power(x1, i - p) * np.power(x2, p)
    return pd.DataFrame(data)
#-----------带惩罚项的代价函数-----------------
def costReg(theta, X, y, l=1):
    # 不惩罚第一项
    _theta = theta[1:]
    reg = (l / (2 * len(X))) * (_theta @ _theta)  # _theta@_theta == inner product

    return cost(theta, X, y) + reg


def gradientReg(theta, X, y, l=1):
    reg = (1 / len(X)) * theta
    reg[0] = 0
    return gradient(theta, X, y) + reg

# -------------1.数据输入及可视化---------------
data2 = pd.read_csv('ex2data2.txt', names=['Test 1', 'Test 2', 'Accepted'])
# -------------2.数据初始化---------------
x1 = data2['Test 1'].values
x2 = data2['Test 2'].values
_data2 = feature_mapping(x1, x2, power=6)  # 增加特征，使边界非线性
X = _data2.values  # 这里因为做特征映射的时候已经添加了偏置项，所以不用手动添加了。
y = data2['Accepted'].values
theta = np.zeros(X.shape[1])
print(X.shape, y.shape, theta.shape)  # ((118, 28), (118,), (28,))
# -------------3.梯度下降---------------
# gradientReg(theta, X, y, 1)
result2 = opt.fmin_tnc(func=costReg, x0=theta, fprime=gradientReg, args=(X, y, 2))
final_theta = result2[0]
# -------------4.结果预测---------------
predictions = predict(final_theta, X)
correct = [1 if a == b else 0 for (a, b) in zip(predictions, y)]
accuracy = sum(correct) / len(correct)
# -------------5.数据可视化---------------
x = np.linspace(-1, 1.5, 250)
xx, yy = np.meshgrid(x, x)
z = feature_mapping(xx.ravel(), yy.ravel(), 6).values
z = z @ final_theta
z = z.reshape(xx.shape)
plot_data()
plt.contour(xx, yy, z, 0)
plt.ylim(-.8, 1.2)
plt.show()